Espai tridimensional
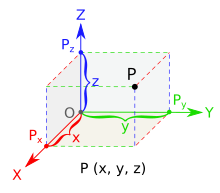
En geometria i anàlisi matemàtica, un objecte o ens és tridimensional si té tres dimensions, és a dir, cadascun dels seus punts pot ser localitzat especificant tres nombres dins d'un cert rang. Per exemple, amplada, longitud i profunditat.[1]
L'espai al nostre voltant és tridimensional a simple vista, però en realitat hi ha més dimensions, de manera que també pot ser considerat un espai tetradimensional si hi incloem el temps com a quarta dimensió.
Espai físic tridimensional
[modifica]En un espai euclidià convencional, un objecte físic finit està contingut dins d'un ortoedre mínim, les dimensions es diuen ample, llarg i profunditat. L'espai físic al nostre voltant és tridimensional a simple vista.[2][3] No obstant això, quan es consideren fenòmens físics com la gravetat, la teoria de la relativitat ens porta a veure que l'univers és un ens tetradimensional que inclou tant dimensions espacials, com el temps, com una altra dimensió. Diferents observadors perceben diferents "seccions espacials" d'aquest espaitemps, per la qual cosa l'espai físic és una mica més complex que un espai euclidià tridimensional.
No es coneix exactament per què el nostre univers sembla tridimensional; més exactament, en les teories actuals no hi ha una raó clara de per què el nombre de dimensions espacials extenses (no compactificades) és igual a tres, encara que existeixen certes intuïcions sobre això: Ehrenfest va assenyalar que en quatre o més dimensions les òrbites planetàries tancades, per exemple, no serien estables (i, per tant, sembla difícil que en un univers així existís vida intel·ligent preguntant per la tridimensionalitat espacial de l'univers). També se sap que hi ha una connexió entre la intensitat d'un camp de forces estàtic amb simetria esfèrica, que satisfà el teorema de Gauss, i la dimensió de l'espai (d), un camp gravitatori, electroestàtic o d'un altre tipus que compleixi aquestes condicions. Per a grans distàncies ha de tenir una variació de la forma:
En què:
- és la intensitat del camp.
- és una constant de proporcionalitat ( per al camp gravitatori).
- és una magnitud extensiva que mesura la capacitat de font per provocar el camp, per a un camp gravitatori coincideix amb la massa i per a un d'elèctric amb la càrrega.
- és la distància al "centre" o font que crea el camp.
- és la dimensió de l'espai.
També, les teories físiques de tipus Kaluza-Klein com les diferents versions de la teoria de cordes, postula que hi ha un nombre de dimensions addicionals compactificades, que només serien observables en experiments amb partícules altament energètiques. En aquestes teories, algunes de les interaccions fonamentals poden ser explicades de manera senzilla postulant dimensions addicionals d'una manera similar a com la relativitat general explica la gravetat. De fet, la proposta original de Theodor Kaluza i Oskar Klein explicava de manera unificada l'electromagnetisme i la gravetat, postulant un univers de 5 dimensions amb una dimensió compactificada (teoria Kaluza-Klein).
Exemples de formes tridimensionals
[modifica]
En geometria, són tridimensionals les següents figures geomètriques:[4]
- Poliedres de cares planes:
- Superfícies corbes:
Totes elles poden ser embegudes en un espai euclidià de tres dimensions. No obstant això, cal assenyalar que tècnicament l'esfera, el con o el cilindre són varietats bidimensionals (només la closca), ja que els punts interiors en aquestes figures no són estrictament part d'aquestes. Només per un abús de llenguatge o extensió d'aquest, informalment es parla d'esferes, cilindres o cons incloent-hi el seu interior.
A més, hi ha la hiperesfera tridimensional (3-varietat), però no és la pela d'una bola sinó la compactificació de amb un punt, així com la 2-esfera és per al pla euclidià .
Sistemes tridimensionals en ciències naturals
[modifica]En química, es parla de sistemes tridimensionals quan l'enllaç químic és igualment intens en les tres direccions de l'espai (per exemple, en el diamant). En magnetisme, es diu que l'ordenament magnètic només és possible si l'acoblament magnètic és tridimensional (és a dir, s'estén en les tres direccions de l'espai). En matemàtiques, el sistema tridimensional es representa en el pla cartesià amb els eixos X, Y i Z. En general, en aquestes representacions s'utilitzen les formes geomètriques de tres dimensions com els cubs o les esferes.
Simulació 3D
[modifica]Avui dia, és possible la simulació mitjançant càlculs basats en la projecció d'entorns tridimensionals sobre pantalles bidimensionals, com ara monitors d'ordinador o televisors. Aquests càlculs requereixen una gran càrrega de procés, per la qual cosa alguns ordinadors i consoles disposen d'un cert grau d'acceleració gràfica 3D gràcies a dispositius desenvolupats per a tal fi. Els ordinadors disposen de les anomenades targetes gràfiques amb acceleració 3D. Aquests dispositius estan formats amb un o diversos processadors (GPU), dissenyats especialment per accelerar els càlculs que suposen reproduir imatges tridimensionals sobre una pantalla bidimensional i d'aquesta forma alliberar de càrrega de procés la CPU o unitat de procés central de l'ordinador.
Geometria
[modifica]Polítops
[modifica]En tres dimensions, hi ha nou polítops regulars: cinc de convexos i quatre de no convexos. Els convexos són els sòlids platònics, mentre que els no convexos són els poliedres de Kepler-Poinsot.
Referències
[modifica]- ↑ Aaron Marcus, Wentao Wang. Design, User Experience, and Usability: Designing Interactions: 7th International Conference, DUXU 2018, Held as Part of HCI International 2018, Las Vegas, NV, USA, July 15-20, 2018, Proceedings, Part II. Springer, 2018, p. 501. ISBN 3319918036.
- ↑ Lino Cabezas Gelabert, Luis Felipe Ortega De uhler. Anàlisi gràfica i representació geomètrica. Edicions Universitat Barcelona, 1999, p. 22. ISBN 8483381192.
- ↑ «Euclidean space | geometry | Britannica» (en anglès). [Consulta: 5 febrer 2022].
- ↑ Four-Dimensional Geometry. MathWorld



















