Cissoide de Diocles

Construcció de la cissioide de Diocles

En geometria, la cissoide de Diocles o simplement, la cissoide, és una corba cúbica plana notable per la propietat que es pot fer servir per construir dues mitjanes proporcionals a una proporció donada. En particular, es pot usar per duplicar un cub. Es pot definir com la corba cissoidal d'una circumferència i una tecta tangent a la circumferència respecte al punt de la circumferència oposat al punt de tangència. De fet, la família de cissoides pren el nom d'aquest exemple i alguns autors s'hi refereixen simplement com la cissoide. Té una cúspide senzilla al pol, i és simètrica respecte al diàmetre de la circumferència que és la línia de tangència de la cúspide. És un membre de la família de les corbes concoides de De Sluze i pel que fa a la forma s'assembla a una tractriu.

La paraula "cissoide" ve del Grec κισσοείδες kissoeides "forma d'heura" de κισσός; kissos "heura" i -οειδές; - oeides "tenint la semblança de". La corba s'anomena en honor de Diocles que la va estudiar al segle ii aC.

Construcció i equacions

Sigui C una circumferència amb diàmetre OA i sigui L la recta tangent a la circumferència a A. Es dibuixa un radi variable R per O que talla C a M₁ i L a M₂. Sigui M el punt a R tal que OM = M₁M₂. Llavors la cissoide es defineix com el lloc geomètric de punts M.

Sigui a el radi de C. Per translació i rotació, es pot fer que O l'origen i el centre del circumferència sigui (a,0), així A és (2a, 0). Llavors les equacions polars de L i C són:

$r=2a\sec \theta$

$r=2a\cos \theta$.

Per construcció, la distància des de l'origen fins a un punt sobre la cissoide és igual la diferència entre les distàncies de l'origen als punts corresponents en L i C. En altres paraules, l'equació polar de la cissoide és

$r=2a\sec \theta -2a\cos \theta =2a(\sec \theta -\cos \theta )$.

Aplicant algunes identitats trigonomètriques, això és equivalent a

$r=2a\sin ^{2}\theta /\cos \theta =2a\sin \theta \tan \theta$.

Si $t=\tan \theta$ en l'equació d'abans. Llavors

$x=r\cos \theta =2a\sin ^{2}\theta ={\frac {2a\tan ^{2}\theta }{\sec ^{2}\theta }}={\frac {2at^{2}}{1+t^{2}}}$

$y=tx={\frac {2at^{3}}{1+t^{2}}}$

són les equacions paramètriques per a la cissoide.

Convertint la forma polar a coordenades cartesianes dona

$(x^{2}+y^{2})x=2ay^{2}$

Construcció per projecció doble

Mecanisme per generar la cissoide

Una altra construcció continua s'obté de la manera següent: Sia una línia L i un punt O que no pertany a L, i sia K la línia que passa per O paral·lela a L. Sia P un punt variable sobre L. Sia Q la projecció de P sobre K, en unes altres paraules Q és la intersecció de K amb la recta que passa per P perpendicular a K. De manera similar sia R la projecció de Q a OP. Llavors la cissoide és el lloc geomètric dels punts R.

Per veure això, sia O l'origen i L la recta x =2a com més amunt. Sia P el punt (2a, 2at), llavors Q és (0, 2at) i l'equació de la recta OP és y =tx. La recta que passa per Q perpendicular a OP és

$t(y-2at)+x=0$.

Per trobar el punt d'intersecció R, es fa y =tx en aquesta equació per aconseguir

$t(tx-2a)+x=0,\ x(t^{2}+1)=2at^{2},\ x={\frac {2at^{2}}{t^{2}+1}}$

$y=tx={\frac {2at^{3}}{t^{2}+1}}$

que són les equacions paramètriques donades a dalt.

Aquesta construcció suggereix el mecanisme mostrat a la dreta per generar la corba.

La construcció de Newton

La construcció de Newton

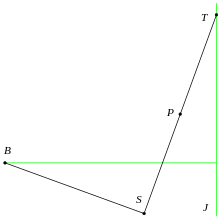
La construcció següent la va obtenir Isaac Newton. Sia J una recta i B un que no pertany a J. Sia BST un angle recte que es mou de manera que ST és igual a la distància de B a J i T roman a J, mentre l'altra cama BS llisca al llarg de B. Llavors el punt mitjà P de ST descriu la corba.

Per veure-ho, sia 2a la distància entre B i J. Per translació i rotació, s'agafa B = (−a, 0) i J la recta x =a. Sia P = (x, y) i sia ψ l'angle entre SB i l'eix x; aquest és igual a l'angle entre ST i J. Per construcció PT = a, per tant la distància de P a J és a sin ψ. En altres paraules a - x = a sin ψ. També SP = a és la coordenada y de (x, y) si es gira un angle ψ, així a = (x+a) sin ψ + y cos ψ. Després de simplificar, això produeix les equacions paramètriques

$x=a(1-\sin \psi ),\,y=a{\frac {(1-\sin \psi )^{2}}{\cos \psi }}.$

Canviant paràmetres substituint ψ pel seu complementari s'obté

$x=a(1-\cos \psi ),\,y=a{\frac {(1-\cos \psi )^{2}}{\sin \psi }}$

o aplicant les fórmules de d'angle doble,

$x=2a\sin ^{2}{\psi \over 2},\,y=a{\frac {4\sin ^{4}{\psi \over 2}}{2\sin {\psi \over 2}\cos {\psi \over 2}}}=2a{\frac {\sin ^{3}{\psi \over 2}}{\cos {\psi \over 2}}}.$

Però això és l'equació polar

$r=2a\sin ^{2}\theta /\cos \theta$

donada més amunt amb θ=Ψ/2.

Fixeu-vos que, com amb la construcció de projecció doble, això es pot adaptar per produir un dispositiu mecànic que genera la corba.

Problema de Delian

El geòmetra grec Diocles va fer servir la cissoide per obtenir dues mitjanes proporcionals a una raó aritmètica donada. Això significa que donades les llargades a i b, la corba es pot fer servir per trobar u i v de manera que u/a=v/u=b/v. Com a cas especial, això es pot fer servir per resoldre el Problema de Delian: en quina magnitud s'ha d'allargar l'aresta d'un cub per doblar el seu volum? Específicament, si a és el costat d'un cub, i b =2a, llavors el volum d'un cub de costat u és

$u^{3}=a^{3}({\tfrac {u}{a}})^{3}=a^{3}({\tfrac {u}{a}})({\tfrac {v}{u}})({\tfrac {b}{v}})=a^{3}({\tfrac {b}{a}})=2a^{3}$

així u és el costat d'un cub amb doble volum del cub original. Fixeu-vos tanmateix que aquesta solució no cau dins de les regles de construcció amb regle i compàs, ja que depèn de l'existència de la cissoide.

Siguin a i b donats. Es demana trobar u de manera que u³=a²b, donant u i v =u²/a com les mitjanes proporcionals. Sia la cissoide

$(x^{2}+y^{2})x=2ay^{2}$

construïda com s'ha explicat a dalt, amb O l'origen, A el punt (2a, 0), i J la recta x =a, donada també a dalt. Sia C el punt d'intersecció de J amb OA. A partir de la llargada donada b, es marca B en J de manera que CB =b. Es dibuixa BA i sia P = (x, y) el punt on talla la cissoide. Es dibuixa OP i ess troba la intersecció amb J a U. Llavors u =CU és la llargada que se cercava.

Per veure-ho, es reescriu l'equació de la corba com

$y^{2}={\frac {x^{3}}{2a-x}}$

i sia N = (x, 0), així PN és la perpendicular a OA per P. A partir de l'equació de la corba,

$PN^{2}={\frac {ON^{3}}{NA}}.$

A partir d'aquí,

${\frac {PN^{3}}{ON^{3}}}={\frac {PN}{NA}}.$

Per semblança de triangles PN/ON =UA/OA i PM/MA =BO/OA. Per tant l'equació esdevé

${\frac {UA^{3}}{OA^{3}}}={\frac {BO}{OA}},$

així

${\frac {u^{3}}{a^{3}}}={\frac {b}{a}},\,u^{3}=a^{2}b$

com es demanava.

Diocles no va resoldre realment el problema de Delian. La raó és que la cissoide de Diocles no es pot construir perfectament, amb regle i compàs. Per construir la cissoide de Diocles, es pot construir un nombre finit dels seus punts individuals, llavors connectar-los tots per formar una corba. El problema és que no hi ha cap manera ben definida de connectar els punts. Si estan connectats per segments de recta, llavors la construcció serà ben definida, però no serà una cissoide de Diocles exacta, sinó només una aproximació. De la mateixa manera, si els punts estan connectats amb arcs circulars, la construcció serà ben definida, però incorrecta. O es podria simplement dibuixar una corba directament, provant a ull la forma de la corba, però el resultat només seria un tempteig imprecís.

Una vegada que s'han dibuixat el conjunt finit de punts sobre la cissoide, llavors la recta PC probablement no tocarà un d'aquests punts exactament, però passarà entre ells, intersecant la cissoide de Diocles en algun punt la localització exacta del qual no s'ha construït, sinó que només s'ha aproximat. Una alternativa és continuar afegint punts construïts a la cissoide que siguin més i més propers a la intersecció amb la recta PC, però el nombre de passos pot molt ben ser infinit, i els grecs no acceptaven aproximacions com límits de passos infinits (així estaven molt confosos per les paradoxesde Zenó).

Un també es podria construir una cissoide de Diocles per mitjà d'una eina mecànica dissenyada de manera especial per aquest propòsit, però això viola la regla de només fer servir compàs i regla. Aquesta regla s'establia per raons de — lògica — axiomàtica — consistència. Permetre la construcció amb eines noves seria com afegir-hi nous axiomes, però els axiomes se suposa que són simples i evidents, però aquestes eines no ho són. Així per les regles de la geometria clàssica, Diocles no va resoldre el problema de Delian, que de fet no pot ser resolt amb aquests mitjans.

D'altra banda, si s'accepta que les cissoides de Diocles existeixin, llavors ha d'existir com a mínim un exemple de tal cissoide. Llavors aquesta cissoide es podria traslladar, girar, i expandir o contreure en mida (sense canviar la seva forma proporcional) a voluntat per encabir-se a qualsevol posició. Llavors s'admetria immediatament que tal cissoide es pot fer servirr per resoldre correctament el problema de Delian.

Ruleta

Aquesta corba és també una ruleta. Agafant dues paràboles congruents, es posen a tocar pels vèrtex, i fent-ne rodar una damunt de l'altre; el vèrtex de la paràbola que roda ressegueix la cissoide.

La cissoide de Diocles com a ruleta. Un parell de paràboles enfrontades l'una amb l'altre simètricament: una damunt i l'altre davall. Llavors es fa rodar la primera paràbola sense lliscar damunt de l'inferior, i les seves successives posicions es mostren en l'animació. Llavors el camí resseguit pel vèrtex de la primera paràbola mentre roda és una ruleta mostrada en vermell, que resulta ser una cissoide de Diocles.

Es defineixen un parell de paràboles les equacions de les quals són

$y=x^{2},\$

$y=-x^{2}.\$

Aquestes paràboles s'enfronten l'una amb l'altra simètricament a banda i banda de l'eix x, (són les que es mostren a la Figura 1). Llavors es tria un punt (a, a²) de la primera paràbola. El pendent de la tangent a la primera paràbola en aquest punt és

${d(x^{2}) \over dx}=2x.\$

La distància mesurada al llarg de la primera paràbola des de punt (0,0) al punt (a, a²) és equivalent a la distància mesurada al llarg de la paràbola inferior des de punt (0,0) al punt (a, −a²). Així, quan roda la primera paràbola, el seu punt que era originalment a (a, a²) vindrà finalment a fer contacte tangencial amb el punt (a, −a²) de la paràbola inferior. Això és vcert per a tots els valors de a.

Quan els dos tals punts estan en contacte, les seves tangents coincideixen i tenen el mateix pendent, que és −2 a. Sia θ l'angle que el pendent 2 a forma amb l'eix x, de manera que

$\tan \theta =2a\qquad \qquad (1)$.

Llavors la primera paràbola ha de girar un angle de 2 θ per tal que el seu punt originalment a (a, a²) vagi a contactar amb la paràbola inferior al punt (a, −a²).

Aquesta rotació es pot realitzar per mitjà de la matriu de rotació R(−2 θ).

$R(-2\theta )={\begin{bmatrix}\cos 2\theta &\sin 2\theta \\-\sin 2\theta &\cos 2\theta \end{bmatrix}}.$

Sia el punt que pivota de la rotació el punt (a, a²). Aquest vector que pivota s'ha de restar de tots els punts de la primera paràbola abans que tots aquests punts s'operin per la matriu de rotació. Llavors, després que la rotació es realitzi, aquest punt que pivota estarà a l'origen, i el pendent de la primera paràbola girada a l'origen serà −2 a, que correspon al pendent del punt (a, −a²) de la paràbola inferior. Aquests dos punts han d'estar en contacte, així la primera paràbola girada es desplaçarà per vector (a, −a²) a la seva posició nova en contacte amb la paràbola inferior. Així la primera paràbola girada es descriurà per

${\begin{bmatrix}\cos 2\theta &\sin 2\theta \\-\sin 2\theta &\cos 2\theta \end{bmatrix}}{\begin{bmatrix}x-a\\x^{2}-a^{2}\end{bmatrix}}+{\begin{bmatrix}a\\-a^{2}\end{bmatrix}}$

on a es pot anomenar un "paràmetre rodador" i x és l'abscissa pregirada.

Aplicant les identitats trigonometriques

$\cos \,2\theta =2\cos ^{2}\theta -1\$

$\sin \,2\theta =2\sin \theta \cos \theta \$

dona un lloc geomètric de punts de la forma

${\begin{bmatrix}2\cos ^{2}\theta -1&2\sin \theta \cos \theta \\-2\sin \theta \cos \theta &2\cos ^{2}\theta -1\end{bmatrix}}{\begin{bmatrix}x-a\\x^{2}-a^{2}\end{bmatrix}}+{\begin{bmatrix}a\\-a^{2}\end{bmatrix}},$

que, a través de l'aplicació de l'equació (1), es converteix en

${\begin{bmatrix}2\cos ^{2}(\tan ^{-1}(2a))-1&2\sin(\tan ^{-1}(2a))\cos(\tan ^{-1}(2a))\\-2\sin(\tan ^{-1}(2a))\cos(\tan ^{-1}(2a))&2\cos ^{2}(\tan ^{-1}(2a))-1\end{bmatrix}}{\begin{bmatrix}x-a\\x^{2}-a^{2}\end{bmatrix}}+{\begin{bmatrix}a\\-a^{2}\end{bmatrix}}.$

Llavors, aplicant les identitats

$\cos \tan ^{-1}x={1 \over {\sqrt {1+x^{2}}}}$

$\sin \tan ^{-1}x={x \over {\sqrt {1+x^{2}}}}$

produeix el conjunt de punts de la forma

${\begin{bmatrix}{2 \over 1+4a^{2}}-1&2\left({2a \over {\sqrt {1+4a^{2}}}}\right)\left({1 \over {\sqrt {1+4a^{2}}}}\right)\\-{4a \over 1+4a^{2}}&{2 \over 1+4a^{2}}-1\end{bmatrix}}{\begin{bmatrix}x-a\\x^{2}-a^{2}\end{bmatrix}}+{\begin{bmatrix}a\\-a^{2}\end{bmatrix}}$

$={\begin{bmatrix}{1-4a^{2} \over 1+4a^{2}}&{4a \over 1+4a^{2}}\\{-4a \over 1+4a^{2}}&{1-4a^{2} \over 1+4a^{2}}\end{bmatrix}}{\begin{bmatrix}x-a\\x^{2}-a^{2}\end{bmatrix}}+{\begin{bmatrix}a\\-a^{2}\end{bmatrix}}$

$={\begin{bmatrix}{(1-4a^{2})(x-a)+4a(x^{2}-a^{2}) \over 1+4a^{2}}+a\\{-4a(x-a)+(x^{2}-a^{2})(1-4a^{2}) \over 1+4a^{2}}-a^{2}\end{bmatrix}}$

$={\begin{bmatrix}{4a^{3}+4ax^{2}-4a^{2}x+x \over 1+4a^{2}}\\{2a^{2}+x^{2}-4a^{2}x^{2}-4ax \over 1+4a^{2}}\end{bmatrix}}.$

El vèrtex de la primera paràbola feta rodar s'especifica fent x = 0, que ocasiona el conjunt de punts que depenen només del paràmetre rodador a i les coordenades del qual són

$X(a)={4a^{3} \over 1+4a^{2}},\qquad \qquad (2)$

$Y(a)={2a^{2} \over 1+4a^{2}}.\qquad \qquad (3)$

Aquesta corba de punts (X(a), Y(a)) és la ruleta, i ara només queda demostrar que és una cissoide de Diocles. La ruleta és una cissoide l'equació de la qual és

$X^{2}={Y^{3} \over {1 \over 2}-Y}\qquad \qquad (4)$.

Per demostrar-ho, es fiquen els valors de X i Y donats per les equacions (2) i (3) a l'equació (4) i es veu si condueix a una tautologia:

$\left[{4a^{3} \over 1+4a^{2}}\right]^{2}={\left[{2a^{2} \over 1+4a^{2}}\right]^{3} \over {1 \over 2}-\left[{2a^{2} \over 1+4a^{2}}\right]}$

${16a^{6} \over (1+4a^{2})^{2}}={\left[{8a^{6} \over (1+4a^{2})^{3}}\right] \over {1 \over 2}-{2a^{2} \over 1+4a^{2}}}$

${16a^{6} \over (1+4a^{2})^{2}}={8a^{6}/(1+4a^{2})^{3} \over {1+4a^{2} \over 2(1+4a^{2})}-{4a^{2} \over 2(1+4a^{2})}}$

${16a^{6} \over (1+4a^{2})^{2}}={8a^{6}/(1+4a^{2})^{3} \over {1 \over 2(1+4a^{2})}}={16a^{6} \over (1+4a^{2})^{2}}$

que és cert per a tots els valors de a, el paràmetre rodador.

La cissoide de Diocles com a corba podària

Teorema: La corba podària d'una paràbola respecte al seu vèrtex és una cissoide de Diocles.

Demostració: Qualsevol paràbola es pot girar i traslladar de manera que acabi sent descrita per l'equació

$y=ax^{2},\,$

el pendent de la qual en punt (x, y) ve donat per la derivada

${dy \over dx}=2ax.$

Llavors el conjunt de punts que formen la recta tangent a la paràbola al punt (b, a b²) és

$L_{1}(b)=\{(b,ab^{2})+(u,2abu)=(b+u,ab^{2}+2abu):u\in \mathbb {R} \}$

i el conjunt de punts que formen la recta que és perpendicular a L₁(b) i que passa a través de l'origen és

$L_{2}(b)=\left\{\left(v,-{v \over 2ab}\right):v\in \mathbb {R} \right\}.$

Observeu que el pendent de L₂(b) és −1/(2ab) que és perpendicular al pendent de L₁(b), 2ab.

La intersecció L₁(b) ∩ L₂(b) es pot trobar establint el següent sistema d'equacions

$b+u=v,\$

$ab^{2}+2abu=-{v \over 2ab}.$

Ara es resol per u:

$ab^{2}+2abu=-{b+u \over 2ab}=-{1 \over 2a}-{u \over 2ab},$

$ab^{2}+{1 \over 2a}=-u\left(2ab+{1 \over 2ab}\right),$

$u={-ab^{2}-{1 \over 2a} \over 2ab+{1 \over 2ab}}={-2a^{2}b^{2}-1 \over 4a^{2}b+{1 \over b}}$

de manera que l'abscissa v és

$v=b+u={2a^{2}b^{2} \over 4a^{2}b+{1 \over b}}$

i l'ordenada és

$-{v \over 2ab}={-ab \over 4a^{2}b+{1 \over b}}.$

Així, el punt d'intersecció és

$\left({2a^{2}b^{2} \over 4a^{2}b+{1 \over b}},{-ab \over 4a^{2}b+{1 \over b}}\right)=\left({2a^{2}b^{3} \over 4a^{2}b^{2}+1},{-ab^{2} \over 4a^{2}b^{2}+1}\right)$

i aquest punt pertany a la corba podària de la paràbola.

Sia

$X={2a^{2}b^{3} \over 4a^{2}b^{2}+1},$

$Y={-ab^{2} \over 4a^{2}b^{2}+1}.$

Llavors la qüestió és: hi ha una constant k que no depèn de b (sinó només d'a) tal que

$X^{2}={Y^{3} \over 2k-Y}$?

Per esbrinar-ho, se substitueixen els valors per X i Y :

${4a^{4}b^{6} \over (4a^{2}b^{2}+1)^{2}}={-a^{3}b^{6}/(4a^{2}b^{2}+1)^{3} \over 2k+{ab^{2} \over 4a^{2}b^{2}+1}}.$

Multiplicant numerador i denominador a la lleia per (4 a² b² + 1)³,

${4a^{4}b^{6} \over (4a^{2}b^{2}+1)^{2}}={-a^{3}b^{6} \over 2k(4a^{2}b^{2}+1)^{3}+ab^{2}(4a^{2}b^{2}+1)^{2}}.$

Multiplicant creuadament,

$8ka^{4}b^{6}(4a^{2}b^{2}+1)^{3}+4a^{5}b^{8}(4a^{2}b^{2}+1)^{2}=-a^{3}b^{6}(4a^{2}b^{2}+1)^{2}.\$

Dividint per (4 a² b² + 1)²,

$8ka^{4}b^{6}(4a^{2}b^{2}+1)+4a^{5}b^{8}=-a^{3}b^{6}.\$

Aplicant la propietat distributiva,

$32ka^{6}b^{8}+8ka^{4}b^{6}+4a^{5}b^{8}=-a^{3}b^{6}.\$

Dividint els dos costats per a³ b⁶,

$32ka^{3}b^{2}+8ka+4a^{2}b^{2}=-1.\,$

Restant 4 a² b² dels dos costats, llavors traient factor comú 8 a k al costat esquerre

$8ak(1+4a^{2}b^{2})=-(1+4a^{2}b^{2}).\,$

S'el·limina el factor comú als dos costats, i llavors es resol per k

$k=-{1 \over 8a}.$

k no depèn de b, així, per a una paràbola donada (amb el valor fix de a), k és una constant, i la corba podària és una cissoide de Diocles.

Corba inversa

La cissoide de Diocles també es pot definir com la corba inversa d'una paràbola amb el centre d'inversió en el vèrtex. Per veure això, considereu la paràbola x =y². En coordenades polars és

$r={\frac {\cos \theta }{\sin ^{2}\theta }}$,

i la corba inversa té per equació

$r={\frac {\sin ^{2}\theta }{\cos \theta }}=\sin \theta \tan \theta$

que és un cas especial de l'equació que defineix la cissoide de Diocles en coordenades polars.

Referències

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Cissoide de Diocles

Bibliografia

• J. Dennis Lawrence. A catalog of special plane curves. Dover Publications, 1972, p. 95,98–100. ISBN 0-486-60288-5. 

Enllaços externs

• Weisstein, Eric W., «Cissoid of Diocles» a MathWorld (en anglès).
• "Cissoid of Diocles" a Visual Dictionary Of Special Plane Curves
• "Cissoid of Diocles" a MacTutor's Famous Curves Index
• "Cissoid" a 2dcurves.com
• "Cissoïde de Dioclès ou Cissoïde Droite" a Encyclopédie des Formes Mathématiques Remarquables (francès)
• "The Cissoid" An elementary treatise on cubic and quartic curves Alfred Barnard Basset (1901) Cambridge pàg. 85ff