Matèria granular

Exemples de matèria granular: esferes de plàstic, grava, llenties i llavors de sèsam.

La matèria granular o granulada és aquella que està formada per un conjunt de partícules macroscòpiques sòlides prou grans perquè l'única força d'interacció entre elles sigui la de fricció. Col·lectivament, aquest tipus de matèria presenta propietats que poden semblar, depenent del tipus de forces a les quals estigui sotmesa, les de l'estat sòlid, l'estat líquid o les del gasós. Una característica important és que la matèria granular tendeix a dissipar ràpidament l'energia de les seves partícules a causa de la força de fricció. Això dona lloc a fenòmens de gran importància com les allaus, els embussos en descàrregues de sitges, entre altres. Com a exemples de matèria granular es troben els grans i llavors, la neu, la sorra, etc.

Encara que la matèria granular és coneguda des de l'antiguitat, l'aparició de fenòmens que aparentment van en contra de la intuïció, com l'efecte de les nous del Brasil, ha fet que en els últims anys s'hagi incrementat el seu estudi per part dels físics. L'estudi d'aquest tipus de materials és molt important pel fet que és el més utilitzat per l'home només després de l'aigua.

Història

L'estudi de la matèria granular es va iniciar ja en temps antics, tot i no haver rebut la mateixa atenció que altres àrees de la física. El registre més antic que es té sobre aquest tema prové del poeta romà Lucreci. Als voltants de l'any 55 aC va escriure:

«

Es poden recollir llavors de rosella amb una cullera amb la mateixa facilitat que si es tractés d'aigua i, en inclinar la cullera, aquestes flueixen d'una forma contínua.

»

Dibuixos realitzats per Ernst Chladni que mostren els patrons formats per sorra col·locada sobre una placa metàl·lica quadrada en ser sotmesa a vibracions.

Al renaixement, Leonardo da Vinci va realitzar experiments que demostraven les lleis de la fricció en sec. Charles de Coulomb, al segle xviii, va escriure l'article Assaig dels màxims i mínims aplicat a problemes d'equilibri relacionats amb l'arquitectura, on exposa observacions i experiments d'equilibri de terraplens i estructures compostes per roques.

Posteriorment, Ernst Chladni, va utilitzar materials granulars col·locats sobre plaques metàl·liques per estudiar les maneres de vibració d'aquestes últimes. Dels seus treballs es va descobrir el que avui es coneix com a figures de Chladni. Un problema relacionat amb l'anterior va ser estudiat per Michael Faraday, qui va investigar la formació de piles de sorra en ser sotmeses a vibracions. William Rankine va estudiar la fricció en materials granulars i, basant-se en els treballs de Coulomb, va establir el que en mecànica de sòls es coneix com a estats actius de Rankine.

Més endavant, diversos investigadors van estudiar la manera com es distribueixen les forces dels grans emmagatzemats en una sitja. I. Roberts va estudiar la dependència de la pressió dels grans contra les parets de la sitja. H. Janssen va descriure com les forces de pressió canviaven de direcció cap a les parets. Lord Rayleigh va establir una analogia entre aquest problema i la resistència a la tracció d'una corda enroscada en un pal.

Cap a finals del segle xix, Osborne Reynolds va realitzar importants descobriments que van contribuir a l'estudi de la matèria granular. A partir d'aquest moment, durant el transcurs del segle XX i fins avui el nombre de científics dedicats a l'estudi de la matèria granular ha anat en augment. Entre ells, un dels més importants ha estat Ralph Bagnold, qui entre 1940 i 1970 va realitzar observacions de les sorres del desert.

Propietats

Mida de partícula

Els anells que envolten el planeta Saturn, compostos de milers de roques, són un exemple de matèria granular on trobem mides de partícula de diversos metres de diàmetre.

Els materials granulars estan compostos d'una gran quantitat de partícules sòlides, les quals són discernibles a primera vista. La grandària de les partícules sol anar des d'algunes micres fins a l'ordre de metres o majors. Com a exemple d'això es dona el cas de les pols, on les partícules són tan petites que amb prou feines es distingeixen a simple vista. En el cas contrari, es poden tenir partícules tan grans com roques, que poden mesurar diversos metres i, fins i tot, asteroides amb formats de diversos centenars de metres.

Forces, acceleracions i energies

La principal propietat de la matèria granular és que l'única força d'interacció que existeix entre les partícules que la componen és la fricció estàtica. Una excepció a això es dona en el cas de les pols més fines, en les quals poden aparèixer interaccions de tipus electroestàtic en carregar elèctricament les seves partícules. L'existència de fricció estàtica com a força predominant entre les partícules d'aquests materials dona lloc a una ràpida dissipació de l'energia cinètica de les partícules, ja que genera col·lisions inelàstiques entre elles. Per aquesta raó, no és possible estudiar la matèria granular amb models de mecànica estadística per a sistemes on hi hagi conservació de l'energia. També significa que la temperatura efectiva d'un material granular és zero i l'única energia de rellevància en aquest tipus de sistemes és l'energia potencial, deguda a la seva posició respecte a un camp gravitacional.

Sobre els medis granulars poden actuar diferents forces externes, les quals són capaces de modificar de forma substancial el seu comportament global. La principal força externa a la qual solen estar sotmesos els materials granulars és la força de gravetat. Aquesta força genera una distribució de tensions a través de les partícules del material. Aquestes tensions donen suport al material i li permeten mantenir una forma definida. D'altra banda, quan el material es deixa relliscar o es deixa caure, la gravetat l'obliga a comportar-se de manera similar a un fluid, com s'observa en els rellotges de sorra.

Si la matèria granular és sotmesa a sacsejades periòdiques, se solen presentar diversos tipus de fenòmens, com ara convecció i segregació de partícules, entre d'altres. La força d'aquestes sacsejades es pot mesurar en termes de l'acceleració que creen. En el cas d'una sacsejada consistent en una oscil·lació periòdica de tipus sinusoidal, l'acceleració mitjana, $\langle a\rangle$, en un cicle és:

$\langle a\rangle ={\frac {2\pi }{T}}\int _{0}^{T}A\omega ^{2}\sin(\omega t)\ {\mbox{d}}t=A\omega ^{2}$,

on T és el període d'oscil·lació, A és l'amplitud d'oscil·lació, $\omega$ és la freqüència angular de l'oscil·lació i t és el temps. L'anterior es pot expressar en termes d'un nombre de Froude, el qual dona una idea de la magnitud de les forces inercials respecte a les forces de gravetat. Per a aquest cas, aquest nombre es pren com una acceleració adimensional denotada per $\Gamma$:

$\Gamma ={\frac {A\omega ^{2}}{g}}$,

essent g el valor de l'acceleració de la gravetat.

Temperatura

Com ja s'ha dit, a causa de la pèrdua gairebé instantània d'energia cinètica de les partícules en la matèria granular, la temperatura efectiva d'aquesta té un valor de zero. No obstant això, si el material granular se sotmet contínuament a forces oscil·lants, com ara sacsejades, les partícules adquireixen una velocitat. A partir d'aquesta velocitat si obtenim la seva mitjana quadràtica, es pot calcular una «temperatura granular», tal com es faria amb un gas ideal:

$V_{\rm {RMS}}={\sqrt {\frac {3kT}{m}}}$

On $v_{\rm {RMS}}$ és la mitjana quadràtica de la velocitat, $k$ és la constant de Boltzmann, $T$ és la temperatura i $m$ és la massa del material.

Tanmateix, és important notar que, quan la força que genera el moviment de les partícules cessa, el medi granular perd la seva energia cinètica de manera gairebé immediata, per la qual cosa, la temperatura torna al seu valor de zero. És per això que no és possible aplicar els principis de la termodinàmica clàssica a la matèria granular. És a dir, clàssicament (vegeu Lleis de la termodinàmica) s'esperaria que l'energia es conservés, l'entropia del sistema augmentés de manera natural i no es pogués assolir la temperatura de zero. No obstant això, cap de les situacions anteriors passa amb la matèria granular.

Per tenir en compte la temperatura d'un medi granular és necessari utilitzar models termodinàmics per a sistemes fora d'equilibri. Molts investigadors de la matèria granular han tendit a no tenir en compte la temperatura granular o menysprear-la, i a eliminar-la de les equacions de moviment. Malgrat tot, altres autors han tractat de mostrar que aquesta temperatura és necessària per descriure aquest tipus de materials.

Polidispersitat

Exemple de matèria granular polidispersa: un bol de kongbap, barreja d'arròs i diverses llavors, comú a la cuina coreana.

A la ciència de polímers, quan es té un conjunt de molècules de polímers de manera que certes molècules tenen major grandària que altres, es diu que el conjunt està polidispers. En el cas dels polímers, és més convenient posar atenció en la diferència entre les masses de les molècules que en la seva mida. L'índex de polidispersitat o polidispersió (PDI, de l'anglès: Polydispersity index) ens dona una idea de la diversitat de molècules existents en una barreja. Aquest índex es calcula dividint la mitjana de masses per pes molecular entre la mitjana de masses per nombre de molècules. És a dir:

$PDI={\frac {M_{w}}{M_{n}}}$.

$M_{w}$, la mitjana de massa per pes molecular es calcula sumant els productes de la massa del total de molècules d'una determinada espècie i la massa d'una molècula d'aquesta espècie fins a tenir en compte tots els tipus de molècules, i dividint aquesta suma entre la massa de totes les molècules. $M_{n}$ és simplement que la suma de les masses de cada molècula es divideixi entre el nombre total de molècules. Quan $PDI=1$, totes les molècules són d'un mateix tipus i es diu que la barreja és monodispersa.

Per analogia, en la matèria granular es defineix una polidispersitat granular. No obstant això, en aquest cas es pren en compte la diferència entre la mida de les partícules en lloc de la diferència en massa. Per calcular la polidispersitat en l'estudi de la matèria granular cal comptar el nombre de partícules que tenen un diàmetre determinat per així obtenir la distribució de diàmetres. La polidispersió, llavors, s'obté calculant la variància d'aquesta distribució:

$PDI=\sigma _{D}^{2}={\frac {\displaystyle \sum _{i=1}^{n}{\bigg (}D_{i}-\langle D\rangle {\bigg )}^{2}}{n}}$,

amb $D_{i}$ el diàmetre d'una determinada partícula, $\langle D\rangle$ el diàmetre mitjana de les partícules, $n$ el nombre total de partícules i $\sigma _{D}^{2}$ la variància de la distribució.

La polidispersió en barreges granulars és molt important pel fet que, en materials polidispersos subjectes a moviments oscil·latoris verticals, solen aparèixer fenòmens de segregació de partícules en què aquestes se separen per mides.

Quan les partícules es distribueixen de forma hexagonal, el material granular aconsegueix la màxima compactació, $\phi =0,74$.

Compactació

Les partícules que componen un material granular poden distribuir-se de diferents maneres dins d'aquest material. Quan es tenen partícules esfèriques, un percentatge del volum del material granular correspon a les esferes en si, mentre que un altre percentatge del volum correspon als buits que es formen entre les partícules. El quocient entre el volum ocupat per les partícules i el volum total del material, les partícules i els buits es coneix com a fracció de volum, representat per $\phi$.

$\varphi ={\frac {V_{\mbox{partícules}}}{V_{\mbox{total}}}}$

La fracció de volum ens dona una idea que com de compacte es troba un material granular. En el cas de materials monodispersos, aquells que solen tenir menor compactació tenen una fracció de volum de prop de 0,56. En sacsejar els materials se solen aconseguir compactacions grans; la màxima compactació assolida per aquesta forma és de 0,68 (en aquest cas es coneix com a empaquetament aleatori compacte o RCP, de l'anglès: Random Close Packing). La màxima compactació possible en materials monodispersos s'assoleix si s'acomoden les partícules de forma hexagonal compacta (HCP, de l'anglès Hexagonal Close Packing). Quan aquest és el cas, la fracció de volum arriba a 0,74.

Quocients entre forces dissipatives

Quan un material granular flueix, diferents forces dissipatives -fricció entre partícules, resistència de l'aire, etc.- es presenten i alteren el seu comportament. Hi ha diferents formes d'analitzar aquests comportaments. Una d'elles és separar les forces dissipatives en quatre classes: col·lisionals, forces de fricció, viscositat i pressió sobre porus. Si es fan quocients entre aquestes forces, s'obtenen els següents nombres adimensionals:

• Nombre de Bagnold: quocient entre forces col·lisionals i forces viscoses.
• Nombre de Savage: quocient entre forces col·lisionals i de fricció.
• Nombre de fricció: quocient entre forces de fricció i forces viscoses.
• Nombre de Darcy: quocient entre forces de fricció i de pressió sobre porus.

Depenent de la manera com es calculi cadascuna d'aquestes forces, s'obtenen diferents fórmules per a cada un d'aquests números, encara que tots ells, d'una manera o altra, depenen de la densitat de les partícules sòlides.

Forma de les partícules

Tot i que la forma més simple d'estudiar la matèria granular és suposar que les partícules que la componen són esfèriques, en molts casos no passa així. En una gran quantitat de situacions, les partícules poden tenir formes diferents d'esfera. Per exemple: els grans de llentia tenen forma d'esferoides oblats, els grans d'arròs tenen forma d'esferoides prolats, els grans de sal comuna tenen forma cúbica, etc.

Quan s'estudien els medis granulars és important tenir en compte la forma de les seves partícules. S'ha descobert que la forma dels grans pot modificar la distribució d'esforços en materials granulars en repòs. Els grans amb forma elongada poden modificar la fricció i fer més difícil el flux del material granular a causa del fet que es perd energia quan roten. D'altra banda, un material compost per esferoides oblats o prolats pot assolir una major fracció de volum que un que estigui compost per esferes.

Comportament

Com ja s'ha explicat anteriorment, la matèria granular exhibeix diferents comportaments depenent del tipus de forces externes a les quals estigui subjecta. Aquests comportaments poden assemblar-se al d'un sòlid, al d'un líquid o al d'un gas. Quan el material es troba en repòs, es comporta com un sòlid. Si el material es troba sota l'acció de la gravetat, el seu comportament és similar al d'un fluid viscós. Sota l'acció d'oscil·lacions periòdiques de baixa acceleració, el material presenta comportaments similars als que presenten els fluids en convecció. En el cas en què el material és subjecte a oscil·lacions d'alta acceleració, aquest s'assembla a un gas les partícules del qual pateixen col·lisions inelàstiques.

Tanmateix, la descripció dels medis granulats no és simple, una gran quantitat de fenòmens que aparenten desafiar la intuïció es presenten, a causa de la naturalesa dissipativa de les forces existeixen en ells.

Matèria granular en repòs

Un material granular es troba en repòs quan la suma de forces que actuen sobre ell i sobre cadascuna de les partícules que el componen és igual a zero. Quan això passa, el comportament del medi granular s'assembla al d'un sòlid. Aquesta semblança, però, sol perdre molt fàcilment amb tan sols aplicar una petita força sobre el material. Un munt de grans, per exemple, pot perdre la seva solidesa i començar a fluir amb tan sols inclinar el material. Depenent de les circumstàncies en què es trobi un material granular en repòs -per exemple, la forma en què s'emmagatzemi- s'observen diferents comportaments que han estat estudiats en major o menor mesura per físics de medis granulars, enginyers, geòlegs, entre d'altres.

Formació de cadenes d'esforços i arcs

Formació de cadenes d'esforç (en blau) unint els punts de contacte de partícules adjacents. El pes de l'esfera vermella és repartit entre diverses partícules del material.

Un material granular es troba en repòs només si la suma de forces sobre cadascuna de les seves partícules és igual a zero (d'acord amb la primera llei de Newton). Perquè això pugui passar, el pes d'una partícula determinada s'ha d'equilibrar amb la força normal i la fricció estàtica degudes a les partícules veïnes. Altrament dit, un gra ha de ser sostingut per les partícules que hi ha a sota seu i als seus costats per evitar caure. Al seu torn, les partícules que hi ha sota d'aquest han d'estar sostingudes per altres de més avall, i així successivament fins a arribar al fons o les parets del recipient. Aquesta successió de forces pot ser vista com una cadena d'esforços, cada part del material granular està sostingut per esforços transmesos de partícula a partícula fins a arribar a la base del contenidor. Així mateix, si s'aplica una força sobre la superfície del medi, aquesta força serà transmesa cap avall i als costats dins del material, repartint entre tots els grans. Això explica per què una persona pot estar-se dreta sobre la sorra: encara que la força deguda al seu pes és gran, aquesta es distribueix entre molts grans.

L'estructura més estable que poden formar un conjunt d'esferes sostingudes per fricció estàtica és una catenària invertida (corba negra).

La transmissió de forces de partícula a partícula només pot donar-se a través del punt de contacte entre els grans. La quantitat de punts de contacte que tenen les partícules entre si depèn molt de la fracció de volum del material granular. Com més separats estiguin els grans els uns dels altres -és a dir, si la fracció de volum és menor, hi haurà menor quantitat de punts de contacte per partícula i la transmissió d'esforços serà menys eficient-. La forma en què es creen les cadenes d'esforços depèn llavors en gran manera de la manera com s'acomoden les partícules en el material. Un lleuger canvi en la compactació del medi provocarà que les cadenes adoptin una altra forma.

Un fenomen associat a la formació de cadenes d'esforç és la formació d'arcs. Quan s'exerceix una pressió suficient sobre un medi granulat, les cadenes d'esforços prenen la forma d'un arc. Gràcies a això, el material pot tenir prou sustentació. La raó per la qual es formen els arcs es pot explicar fent ús del càlcul variacional: es pot demostrar matemàticament que al col·locar una seqüència d'esferes sostingudes mitjançant la fricció estàtica, la forma més estable possible per arreglar és la descrita per una catenària invertida.

Piles de materials granulars

Pila de taní en pols mostrant la típica estructura cònica que formen els medis granulars en apilar.

Quan un conjunt de partícules s'emmagatzemen, sense altra estructura que les sostingui excepte el sòl, les forces de fricció estàtica entre elles obliguen aquest conjunt a formar una estructura cònica. En mecànica, la fricció estàtica d'un material es pot calcular experimentalment col·locant dos objectes -per exemple dos blocs amb superfície plana- fets del mateix material un sobre un altre. Si es comença a inclinar lentament aquest sistema, arribarà un moment en què el bloc superior lliscarà vencent aquesta força de fricció. L'angle d'inclinació teòric, $\theta _{m}$, en el qual es venç aquesta força es calcula de la següent manera:

$\Theta _{m}=\tan ^{-1}\mu _{e}\!$.

El símbol $\mu _{e}$ representa el coeficient de fricció estàtica que depèn principalment de la rugositat del material.

En els materials granulars aquest angle és conegut com a angle de repòs. Aquest angle defineix el pendent màxim que pot tenir una pila de partícules sense que aquestes es precipitin en forma d'allau i és l'angle format entre el sòl i la superfície del turó. Com que la matèria granular no és un medi continu, sinó que està conformat per partícules discretes i buits, la força de fricció no és constant sobre tota la superfície del material. La fracció de volum del material, la forma de les partícules, entre altres factors, influeixen sobre la forma en què la fricció actua. És per això que un angle d'inclinació igual a $\theta _{m}$ no és garantia d'estabilitat en el material. Una petita força sobre seu pot provocar un lliscament dels grans, similar al que s'observa a les allaus de neu. Malgrat això, cap pila de material granular pot existir si l'angle d'inclinació de les seves parets és més gran que l'angle de repòs.

Quan al material granular hi ha altres tipus de forces entre les partícules -que col·lectivament es poden considerar com a forces de cohesió -, com ara les càrregues elèctriques, les partícules tenen major dificultat per a lliscar cap avall, de manera que la pila de partícules pot tenir un major angle d'inclinació i, per tant, l'angle de repòs s'incrementa. Quan això passa, es defineix un angle de fricció interna $\phi \!$ com l'angle que tindria el monticle si dins seu només actuessin les forces de fricció estàtica. En aquest cas, aquest últim angle és sempre menor que l'angle de repòs i, només quan les forces de cohesió són nul·les, tots dos angles coincideixen.

Grans en sitges

En verd: pressió en el fons d'un recipient de 2 m de diàmetre ($\Lambda =1$ m) que conté un material granular amb densitat de 1000 kg/m³ en funció de l'altura d'ompliment. La línia vermella puntejada representa la pressió que exerciria un fluid simple. La línia negra representa la màxima pressió que pot exercir el material.

Quan un fluid és posat en un contenidor cilíndric, és ben sabut que la pressió al fons d'aquest contenidor augmenta en incrementar l'altura fins a la qual és omplert. La pressió hidroestàtica es pot calcular a través de la llei de Stevin de la següent manera:

$P=\rho gh\!$,

on $P$ és la pressió hidroestàtica, $\rho$ és la densitat del fluid, $g$ és el valor de l'acceleració de la gravetat i $h$ és l'altura de la columna de fluid.

En el cas de la matèria granular, s'esperaria que en omplir de grans una sitja -o qualsevol recipient cilíndric- la pressió al fons s'incrementés de la mateixa manera que ocorre per als fluids simples. No obstant això, un material granular deixa d'incrementar la pressió sobre el fons del seu contenidor una vegada que s'aconsegueix una certa alçada. H. A. Janssen va descobrir que la pressió sobre les parets d'un contenidor que alberga un material granular segueix la següent relació:

$P=\Lambda \rho g\left(1-{\rm {e}}^{-h/\Lambda }\right)$.

En aquest cas, $\Lambda$ és un paràmetre que depèn de la fricció estàtica entre les parets de la sitja i els grans i el seu valor sol ser de la magnitud del radi del contenidor. Aquest comportament és conegut com a efecte Janssen.

L'explicació d'aquest efecte està en la manera com es transmeten els esforços entre els grans: depenent de la manera com es distribueixen les partícules, les cadenes d'esforços tendeixen a dirigir la força a causa del pes del material cap a les parets del contenidor. En els fluids simples, la pressió en un determinat punt d'aquests es dirigeix cap a totes les direccions (obeint el principi de Pascal). En canvi, en els medis granulars, la pressió pot seguir diferents camins de contactes fins a arribar a les parets. Per aquesta raó, no hi ha una distribució equitativa en sentit horitzontal i vertical; major quantitat de pressió es dirigeix cap a les parets que cap al fons.

L'efecte Janssen representa un problema per als enginyers, ja que, si aquests calculen la pressió d'un medi granulat sobre la paret d'una sitja com si es tractés d'una pressió hidroestàtica, poden subestimar la resistència que haurien de tenir aquestes parets, i pot arribar a presentar-se fins i tot, una explosió a la sitja.

Dilatància de Reynolds: un recipient de goma ple de sorra i aigua que arriba fins a una certa altura d'un tub de vidre incorporat a ell, en ser comprimit, l'aigua baixa de nivell pel fet que ocupa els espais creats per la compressió sobre la sorra.

Dilatància

Els materials granulars pateixen un canvi en la seva fracció de volum quan estan subjectes a una pressió. El fenomen va ser descrit per primera vegada per l'Osborne Reynolds el 1885. Reynolds va comprovar aquest fenomen omplint un recipient de goma amb sorra i aigua, afegint un tub de vidre a la boca del recipient, de manera que l'aigua arribava a un cert nivell dins del tub. En comprimir amb les mans el contenidor de goma, el nivell de l'aigua en el tub va baixar, en contra del que s'esperaria. Aquest fenomen és conegut com a dilatància de Reynolds.

L'explicació d'aquest fenomen, donada pel mateix Reynolds, consisteix en el canvi en la fracció de volum del material granular. En comprimir la sorra, els grans d'aquesta pateixen un reacomodament en les seves posicions, de manera que augmenta l'espai buit entre les partícules. En ocórrer això, l'aigua ocupa aquests nous espais i baixa el seu nivell. Aquest fenomen és observat també a les platges: en caminar una persona sobre la sorra mullada, les petjades dels peus semblen assecar-se. L'explicació és la mateixa: la pressió deguda al pes de la persona que camina sobre la platja genera un canvi en la fracció de volum de la sorra i l'aigua dins d'ella descendeix de nivell, i la superfice de la sorra apareix seca.

Comportament a baixes acceleracions

Un medi granular que deixa d'estar en repòs, ja sigui a causa de l'acció de la gravetat o sacsejades periòdiques, sol comportar-se, en la majoria de les ocasions, d'una manera molt similar a la d'un fluid. Quan un material granular es mou gràcies a la força de gravetat a través d'un forat (per exemple, en descarregar una sitja o en un rellotge de sorra), es genera un flux de grans, que depenent de la mida i la forma de les partícules pot ser continu o es pot interrompre per embussos de les partícules. D'altra banda, quan un material granular és sotmès a sacsejades periòdiques, se sol presentar un fenomen semblant a la convecció que presenten els fluids simples. Si a més a més, el material està polidispers, s'observa una segregació de partícules per mides, donant lloc a fenòmens com l'efecte de les nous del Brasil.

La transició entre un medi granular estàtic i un de fluent se sol donar en iniciar una força oscil·latòria externa, que ha provocat una fluïdització. Aquest efecte genera la pèrdua de solidesa del material, que provoca que un objecte que es trobi a la superfície del medi s'enfonsi. La fluïdització té un efecte summament destructiu en els terratrèmols, ja que en moure la terra aparentment estable però saturada d'aigua, ocorre una liqüefacció i les construccions que hi ha a la superfície perden suport i col·lapsen en enfonsar-hi.

Un material granular recentment buidat dins del seu contenidor (a) té una fracció de volum molt baixa. Si se sotmet al sistema a vibracions horitzontals, ocorre un reacomodament de partícules, la fracció de volum augmenta, i l'espai buit i el volum total disminueix (b).

Compactació induïda per vibració

Quan un conjunt de grans són buidats dins d'un recipient, el material sol tenir una compactació baixa, amb una fracció de volum de prop de 0,55. Per reduir el volum ocupat pels espais buits, de manera que el material en conjunt ocupi menys espai, el medi ha de ser sotmès a vibracions horitzontals. D'aquesta manera, la fracció de volum augmenta i pot arribar a valors més grans. Amb això és més fàcil emmagatzemar els grans, ja que es requereixen contenidors més petits.

Usualment, la fracció de volum no sol sobrepassar un valor de 0,64. Llevat això, usant diferents configuracions, com ara vibracions horitzontals i verticals combinades, o sistemes de poques partícules, es poden aconseguir compactacions induïdes per vibració amb fraccions més grans que aquest valor. El desavantatge d'això és que la forma del recipient i també un paràmetre del sistema afecten el comportament del material granular, de manera que no es poden considerar casos generals.

Per aconseguir la màxima fracció de volum, 0,74, que correspon a un vidre granular arreglat en forma hexagonal mitjançant vibració ha calgut recórrer a mètodes més sofisticats. Una capa de material granular es col·loca en el buit sobre una placa metàl·lica perforada. D'aquesta manera es força que les partícules caiguin sobre les perforacions i formin un arranjament ordenat. Quan la capa està completa, es col·loca la següent. Si alguna partícula queda desordenada, es retiraria aquesta «imperfecció» a mà. El primer acord perfecte, sense defectes, es va aconseguir per mitjans purament mecànics i sense necessitat d'una intervenció manual, i va ser reportat per Nahmad-Molinari i Ruiz-Suárez el 2002; que van utilitzar una mena de creixement epitaxial. En el seu mètode, utilitzen un recipient amb forma de prisma triangular en el qual posen esferes d'acer d'una en una. El recipient és sacsejat verticalment amb acceleracions lleugerament superiors a la gravetat. Quan una certa quantitat de partícules es troben en el recipient, s'aglomeren causa de les col·lisions inelàstiques entre elles, de manera que es genera un nucli d'esferes en constant contacte entre elles. Les noves partícules que són llançades més recentment s'uneixen a aquest nucli fins que la primera capa es forma. En la següent capa, les partícules ocupen les posicions de repòs entre els buits de les esferes de sota, de manera similar al mètode anterior a aquest. Com que el procés és «d'una en una» i com que el sistema és sotmès a la baixa acceleració, cada esfera «busca» la seva posició i la segona capa es completa. Finalment, la resta de les capes es formen fins a omplir el contenidor.

Convecció granular

Esquema que representa materials granulars sotmesos a agitació vertical. Un recipient cilíndric (esquerra) indueix una convecció granular on els grans pugen pel centre i baixen pels costats. Un recipient cònic (dreta) indueix un moviment convectiu a la inversa que en el primer cas.

En els fluids simples, la convecció ocorre en escalfar la part inferior del medi, que genera una disminució de la densitat del fluid en aquesta regió. Això genera una inestabilitat, on la gravetat que actua sobre el medi entra en competència amb la força d'empenta deguda a aquest canvi de densitat. El resultat és la creació d'un moviment cíclic on el fluid calent puja i el fluid fred descendeix.

La convecció en la matèria granular apareix quan aquesta és sotmesa a vibracions verticals. Aquest fenomen té una aparença molt similar al que s'observa en els fluids simples: una part del material ascendeix, mentre que una altra baixa, i s'estableix una circulació contínua. Tanmateix, el mecanisme que dona lloc a la convecció granular és una mica diferent de la inestabilitat convectiva en els fluids simples. Una gran quantitat d'autors han dedicat temps a estudiar aquest fenomen, i han proposat diversos mecanismes generadors d'aquesta convecció.

Michael Faraday va ser la primera persona a reportar aquest fenomen, en estudiar la formació de monticles en materials granulars sota vibració. Des de llavors s'han fet una gran quantitat d'estudis sobre aquest comportament. S'ha demostrat mitjançant treballs experimentals que l'acceleració límit a la qual comença el moviment col·lectiu del medi granular és lleugerament superior a l'acceleració de la gravetat. Originalment es va proposar que l'origen de la convecció granular es devia a la circulació d'aire entre els grans, que feia que aquests últims ascendissin pel centre del sistema i baixessin per les parets del recipient. Més endavant, es va trobar que les parets del recipient poden generar la suficient força per donar lloc a la convecció. Això va ser confirmat finalment per l'equip d'Edward Ehrichs i col·laboradors de la Universitat de Chicago, que van experimentar amb un material granular sotmès a agitacions verticals i observar el moviment col·lectiu dels grans a través d'imatges per ressonància magnètica nuclear. L'explicació del fenomen es basa en el fet que quan es llencen els grans cap amunt, gràcies a la vibració vertical, aquells que es troben propers a les parets pateixen una major força de fricció deguda a aquestes, i això els impedeix pujar més amunt que les partícules en el centre del recipient. En haver pujat les partícules centrals a major altura, es genera un buit en el fons del recipient que és ocupat pels grans exteriors. D'aquesta manera, en cada cicle el moviment efectiu és una circulació on els grans ascendeixen pel centre i descendeixen per les parets.

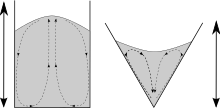
La geometria del recipient influeix també en la manera com es dona la convecció granular. Mentre que en un recipient cilíndric el procés ocorre a la manera com s'ha explicat anteriorment, en un contenidor les parets tenen una certa inclinació, la convecció inverteix el seu sentit de moviment. S'ha observat que si es col·loca un conjunt de grans en un recipient amb forma de con invertit i se sotmet a vibracions verticals, les partícules descendeixen pel centre i ascendeixen per les vores. Aquesta inversió passa pel fet que la inclinació de les parets redueix el contacte i, per tant, la fricció entre aquestes i els grans. En ser llançats cap amunt, els grans que es troben a les zones exteriors se separen entre si i tornen a la paret en un punt més alt que on han començat. D'aquesta forma, el material exterior és empès més cap a fora i cap amunt que el material central, fet que genera aquesta «convecció inversa».

Segregació granular

Un exemple del mecanisme de l'efecte de les nous del Brasil. Un «intrús» col·locat dins d'un material granular tendeix a pujar quan el granulat és sotmès a agitacions verticals. L'intrús ha de tenir un diàmetre major que el de les partícules que conformen el medi granular.

Un efecte molt important en la matèria granular és la segregació granular. Quan una barreja polidispersa de grans és sacsejada verticalment, les partícules se separen per mides, i les més grans queden a la part superior i les més petites a la part inferior. Això passa fins i tot si les més grans tenen major massa que les petites. Això sembla que desafia els principis físics; s'esperaria que les partícules amb més massa descendissin, mentre que les de menor massa romanguessin a la part superior, de manera que es reduiria l'energia potencial. Aquest fenomen va ser batejat com a efecte de les nous del Brasil pel fet que en una barreja de nous, les nous del Brasil solen ser les de major massa i, per tant, apareixen sempre en la superfície de la barreja després que aquesta ha estat sacsejada.

Diversos autors s'han dedicat a l'explicació d'aquest fenomen. La primera explicació, que va fer Anthony Rosato, sostenia que l'ascens de les partícules grans es devia a la infiltració de partícules petites sota d'aquesta. En el moment en què el sistema es mou cap amunt, la partícula gran genera un buit sota seu que és ocupat per les petites. En canviar de direcció el moviment del sistema, els grans que recentment van ocupar aquest espai impedeixen a la partícula major descendir. Això genera un moviment net cap amunt. Altres autors van proposar que la segregació granular era deguda a la convecció, la qual arrossega la partícula gran cap amunt. A causa de la seva mida, aquesta última no pot baixar com ho farien les petites, ja que el flux cap avall es realitza per un espai molt prim proper a les parets.

Mathias Möbius i col·laboradors de la Universitat de Chicago van demostrar que el temps d'ascens depèn de la densitat de les partícules de major grandària. Quan aquestes últimes tenen una densitat semblant a la dels grans menors, el temps que els pren arribar a la superfície és major. Aquest temps es redueix si la seva densitat s'incrementa o disminueix respecte a la densitat dels grans petits. Aquest fet va capgirar completament el problema: la convecció i la infiltració eren insuficients per explicar la segregació granular. A partir d'això, es van proposar models basats en la inèrcia de les partícules: Aquells grans amb major massa, tindrien major energia cinètica i, com a conseqüència, podrien realitzar més treball en contra de la fricció del granulat, penetrant una longitud major. Per a aquelles partícules amb majors densitats es podia explicar el fenomen degut simplement a una força de flotació.

Una nova complicació va sorgir en descobrir que, si es col·locava una barreja granular al buit, el temps d'ascens de les partícules més grans es convertia en el mateix per a totes. A mesura que es redueix la pressió d'aire en el granulat, la diferència entre els temps d'ascens es redueix, fins a esdevenir iguals en el buit. A partir d'això, es va suggerir que el gradient de pressions dins el medi granular jugava un rol important en el fenomen de la segregació. Per poder descriure correctament aquesta última cal tenir en compte totes les variables descrites pels diferents autors.

En certes circumstàncies es pot tenir un efecte de les nous del Brasil invers. En aquest cas les partícules de major grandària es precipiten al fons del recipient. Aquest efecte va ser predit primerament a través de simulacions en ordinador. No obstant això, alguns autors posaven en dubte la seva existència a causa de la falta d'evidència experimental, fins que finalment es va poder confirmar de forma definitiva. L'efecte de les nous del Brasil invers sol succeir quan s'introdueix una partícula més gran, però menys densa a una profunditat molt propera al fons del recipient. Aquest fenomen s'ha pogut explicar, igual que l'efecte convencional, amb un gradient de pressions.

Un material granular s'encalla quan tracta de passar a través d'una tremuja a causa de la formació d'arcs (esferes vermelles).

Fluxos granulars i embussos

Si un contenidor de matèria granular és perforat a la part inferior, els grans dins seu fluiran cap a fora. Molts factors intervenen en la forma d'aquest flux, el qual pot ser constant o interrompre's sobtadament. Com a exemples d'això, en un rellotge de sorra el flux és pràcticament constant, mentre que un saler cal sacsejar-lo per extreure els grans.

Als líquids que escapen a través d'un orifici, la velocitat del flux depèn principalment de l'altura a la qual arriba el líquid dins el recipient. El fenomen s'explica a través del teorema de Torricelli i és causa de l'augment de la pressió hidroestàtica en el fons del recipient en augmentar l'altura del fluid. Als medis granulats, però, la pressió deixa d'incrementar-se quan el material aconsegueix una altura d'aproximadament dues vegades el diàmetre del recipient. Això provoca que, durant la major part de la descàrrega dels grans, el flux surti amb la mateixa velocitat, que es redueix només quan el contenidor està gairebé buit.

En alguns casos el flux granular és interromput per l'embús de partícules en l'orifici de sortida. Quan aquesta obertura té un diàmetre molt petit, encara que major que el dels grans, el material s'hi encalla i interromp el flux. La raó d'aquests embussos és que en tractar diverses partícules de sortir a la vegada, es forma un arc en el forat. Atès que els arcs tenen una gran estabilitat, els grans queden impossibilitats per moure's, gràcies a la fricció estàtica, i obstrueixen la sortida. L'única forma de restablir el flux és retirar un dels grans en l'arc, sigui manualment o aplicant una força sobre el sistema. S'ha demostrat per mitjans experimentals que les interrupcions en les descàrregues de grans esfèrics es donen quan l'orifici de sortida té un diàmetre menor a aproximadament 4,5 vegades el diàmetre de les partícules. Amb obertures majors a aquest valor el flux es torna constant. Si els grans no són esfèrics, el diàmetre del forat al qual no es presenten embussos pot ser diferent.

Gasos granulars

En un gas granular que s'inicia amb una distribució uniforme s'agrupen partícules en estructures en forma de cadenes (partícules vermelles), al voltant de les quals s'acumulen més partícules.

La matèria granular sotmesa a altes acceleracions sol comportar-se de manera similar que un gas molecular teòric. En aquests últims les molècules que els formen pateixen col·lisions elàstiques i es pot suposar una conservació de l'energia com ocorre en la teoria dels gasos ideals. Tanmateix, aquest no és el cas per als medis granulars. Cada partícula perd una part de la seva energia cinètica en xocar contra una altra, i es converteix aquesta energia en calor, so, vibració, rotació o una altra forma d'energia (és a dir, ocorre un xoc inelàstic). La quantitat d'energia perduda en cada col·lisió depèn del coeficient de restitució del material que compon el gra. Quan es considera el sistema granular com a conjunt, la pèrdua d'energia depèn del nombre de col·lisions ocorregudes en un determinat temps. Com a exemple, si es deixa caure una bala dins d'un recipient de vidre, aquesta rebotarà un cert nombre de vegades fins que finalment s'aturarà. No obstant això, si es deixa caure una gran quantitat d'aquests objectes a la vegada dins del mateix recipient, el sistema en conjunt s'aturarà gairebé instantàniament, pel fet que el nombre de col·lisions és molt més gran.

Perquè un medi granulat presenti un comportament semblant al d'un gas ha d'estar sotmès a una força constant prou gran. Si la força que el manté en aquest estat s'atura sobtadament, el material arribarà al repòs de forma gairebé immediata. A més si l'acceleració no és prou elevada, el material disposarà d'un cert temps per relaxar-se, i el seu comportament semblarà el d'un líquid (vegeu la secció «Convecció granular»).

El caràcter dissipatiu de les col·lisions fa que els gasos granulars siguin sistemes fora d'equilibri termodinàmic. Aquest fet genera certs fenòmens que a primera vista semblarien violar les lleis de la termodinàmica, si el sistema és estudiat d'una manera simple sense considerar aquestes pèrdues d'energia. Entre els fenòmens que apareixen en aquests medis es poden esmentar l'aglomeració granular, la ruptura de l'equipartició de l'energia i el col·lapse inelàstic.

Col·lapse inelàstic

Com que a la matèria granular les col·lisions entre partícules són essencialment inelàstiques, la quantitat d'energia dissipada durant un cert temps depèn del nombre de xocs ocorreguts en aquest lapse. Com més gran sigui aquest nombre de col·lisions, és major l'energia que el sistema perd. En un gas granular, les col·lisions ocorren de forma aleatòria. Normalment s'esperaria que de mitjana el nombre de col·lisions per unitat de temps en una zona determinada del gas sigui igual al nombre de col·lisions en una altra zona de la mateixa mida que la primera en el mateix temps. No obstant això, aquest nombre està subjecte a fluctuacions estadístiques, i per això existeix la probabilitat que en una determinada zona, per un moment ocorrin un nombre de xocs lleugerament més gran que en una altra. Així s'aconsegueix una major pèrdua d'energia a aquesta regió, fet que resulta en una disminució en la velocitat de les partícules. En ocórrer això, la pressió exercida per les mateixes disminuirà, i provocarà que altres partícules que no es trobaven en aquesta zona hi entrin, de manera que s'incrementarà encara més la quantitat de col·lisions i la pèrdua d'energia. Al final, el gas granular presentarà un aspecte no homogeni, amb algunes regions amb densitats molt baixes amb partícules movent-se a gran velocitat, i altres poblades amb una gran quantitat de grans aglomerats els uns contra els altres.

El col·lapse inelàstic va ser observat per primera vegada en simulacions per ordinador en una dimensió i posteriorment, en més dimensions. L'efecte ocorre en les simulacions en augmentar el nombre de col·lisions per unitat de temps entre dues partícules; quan aquestes perden energia i són empeses l'una contra l'altra per la resta de les partícules, comencen a rebotar cada vegada més ràpidament fins que els xocs entre elles es tornen infinits, i provoquen un «col·lapse» en la simulació. Aquest fenomen provoca la formació d'estructures en forma de cadenes i filaments, que tenen una gran similitud amb l'estructura de l'univers a gran escala.

Bibliografia

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Matèria granular

• Duran, J., Reisinger A., Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials. Novembre de 1999, Springer-Verlag New York, Inc, New York, ISBN 0-387-98656-1.
• Aste, Tomaso, Di Matteo, T.; Tordesillas, A. Granular and complex materials. 2007, World Scientific, ISBN 981-277-198-0.
• Resnick, Robert; Halliday; Krane, Kenneth S. Física Vol 1. 4a edició. Companyia Editorial Continental, 2001. ISBN 968-26-1230-6.