Hipòtesi de Riemann
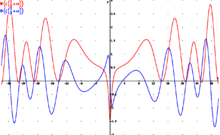

En matemàtiques pures, la hipòtesi de Riemann, formulada per primera vegada per Bernhard Riemann l'any 1859, és una conjectura sobre la distribució dels zeros de la funció zeta de Riemann ζ(s).[1]
La hipòtesi de Riemann, per la seva relació amb la distribució dels nombres primers en el conjunt dels naturals, és un dels problemes oberts més importants en les matemàtiques contemporànies.[2] La hipòtesi de Riemann i algunes de les seves generalitzacions, juntament amb la conjectura de Goldbach i la conjectura de nombres primers bessons, conformen el vuitè problema de Hilbert a la llista de vint-i-tres problemes no resolts de David Hilbert ; també és un dels problemes del Millennium Prize del Clay Mathematics Institute, que ofereix un milió de dòlars a la primera persona que desenvolupi una demostració correcta de la conjectura.[3] El nom també s'utilitza per a alguns anàlegs estretament relacionats, com la hipòtesi de Riemann per a corbes sobre camps finits.
La funció zeta de Riemann ζ(s) és una funció on l'argument s pot ser qualsevol nombre complex diferent de l'1, i els valors de la qual també són complexos. Té zeros als nombres enters parells negatius; és a dir, ζ(s) = 0 quan s és un de −2, −4, −6, . . .. Aquests s'anomenen els seus zeros trivials. La funció zeta també és zero per a altres valors de s, que s'anomenen zeros no trivials. La hipòtesi de Riemann es refereix a les ubicacions d'aquests zeros no trivials i afirma que:
| « | La part real de cada zero no trivial de la funció zeta de Riemann és 12. | » |
Així, si la hipòtesi és correcta, tots els zeros no trivials es troben a la línia crítica que consta dels nombres complexos 12 + it, on t és un nombre real i i és la unitat imaginària.
Definició[modifica]
La funció zeta de Riemann ζ(s) està definida en els nombres complexos com la suma d'una sèrie infinita de la següent forma:
i és convergent quan la part real és estrictament més gran que 1. Leonhard Euler (que va morir 43 anys que nasqués Riemann) va demostrar que aquesta sèrie equival al producte d'Euler:
on el producte infinit s'estén sobre el conjunt dels nombres primers p, i novament es convergeix per a nombres complexos s amb part real més gran que 1. La convergència del producte d'Euler mostra que ζ(s) no té zeros en aquesta regió, ja que cap dels factors té zeros. La hipòtesi de Riemann tracta dels zeros fora de la regió de convergència de la suma de la sèrie descrita anteriorment i del producte d'Euler associat. Per tal de preservar el sentit d'aquesta hipòtesi cal prolongar analíticament la funció zeta de Riemann ζ(s) de tal forma que tingui sentit per a qualsevol valor de s. En particular, es pot expressar mitjançant la següent equació funcional:
vàlida per a tots els nombres complexos excepte per a s = 1, on la funció té un pol. Com s'ha dit anteriorment, la hipòtesi de Riemann tracta dels zeros d'aquesta versió de la funció zeta estesa analíticament. La funció té uns certs valors, anomenats zeros "trivials", per als quals la funció zeta s'anul·la. De l'equació es pot veure que s = −2, s = −4, s = −6, .[4] (tots els enters parells negatius) són zeros trivials. Així mateix, existeixen altres valors complexos s, que compleixen la condició 0 < Re(s) < 1, per als quals la funció zeta també s'anul·la, són els anomenats zeros "no trivials". La conjectura de Riemann fa referència a aquests zeros no trivials en afirmar que:
| la part real de qualsevol zero no trivial de la funció zeta de Riemann és igual a 1/2. |
Per tant, els zeros no trivials haurien de trobar-se en la línia crítica s = 1/2 + i t, on t és un nombre real i i és la unitat imaginària. La funció zeta de Riemann, al llarg de la línia crítica ha estat estudiada en termes de la funció Z, els zeros de la qual corresponen als zeros de la funció zeta sobre la recta crítica.
Història[modifica]
| « | "...es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien." ("…és molt probable que totes les arrels seran reals. Clar que es voldria tenir una demostració rigurosa; Per ara, després d'alguns intents fugaços en va, he posposat la seva recerca, ja que sembla ser prescindible per aconseguir un objectiu immediat de la meva recerca.") |
» |
| — Afirmació de Riemann sobre la hipòtesi de Riemann, de (Riemann 1859). (Aquí parla d'una versió de la funció zeta de Riemann, modificada perquè les seves arrels (zeros) siguin reals en lloc d'estar en la línia crítica.) | ||
Riemann va mencionar la conjectura l'any 1859, que seria anomenada la hipòtesi de Riemann, en la seva tesi doctoral Sobre els nombres primers menors que una magnitud donava, en desenvolupar una fórmula explícita per calcular la quantitat de primers menors que x. Com que no era essencial per al propòsit central del seu article, no va intentar desenvolupar-ne una demostració. Ell sabia que els zeros no trivials de la funció zeta estan distribuïts al llarg de la recta s = 1/2 + i t, i sabia també que tots els zeros no trivials havian d'estar en el rang 0 ≤ Re(s) ≤ 1.[5]
L'any 1896, Hadamard i de la Vallée-Poussin van demostrar, independentment, que cap zero no es podia trobar sobre la recta Re(s) = 1. Juntament amb les altres propietats dels zeros no trivials demostrades per Riemann, aquest resultat va demostrar que tots els zeros no trivials han d'estar en l'interior de la banda crítica 0 < Re(s) < 1. Aquest va ser un pas fonamental per a les primeres demostracions del teorema dels nombres primers.
L'any 1900, Hilbert va incloure la hipòtesi de Riemann en la seva famosa llista dels 23 problemes no resolts — és part del problema 8, juntament amb la conjectura de Goldbach. Quan se li va preguntar què faria si es despertés després d'haver dormit cinc-cents anys, Hilbert va respondre que la seva primera pregunta seria si la hipòtesi de Riemann havia estat demostrada. La hipòtesi de Riemann és l'únic problema dels que va proposar Hilbert que forma part del premi del mil·lenni de l'Institut Clay de Matemàtiques.
L'any 1914, Hardy va demostrar que existeix un nombre infinit de zeros sobre la recta crítica Re(s) = 1/2. No obstant això, encara era possible que un nombre infinit (o fins i tot la majoria) dels zeros no trivials es trobés en algun altre lloc dins de la banda crítica. En treballs posteriors, Hardy i Littlewood l'any 1921 i Selberg l'any 1942 van donar estimacions de la densitat mitjana dels zeros sobre la línia crítica.
La major part de la comunitat matemàtica pensa que la conjectura és correcta, tot i que altres grans matemàtics com Littlewood i Selberg es van mostrar escèptics, si bé l'escepticisme de Selberg va anar disminuint des de la seva joventut. En un article de 1989 va suggerir que un anàleg ha de ser cert per una classe molt més àmplia de funcions (la classe de Selberg). Treballs recents s'han concentrat en el càlcul explícit de la localització de grans quantitats de zeros (amb l'esperança de trobar algun contra-exemple) i en l'establiment de cotes superiors en la proporció de zeros que puguin estar lluny de la línia crítica (amb l'esperança de reduir-les a zero).
Al setembre de 2018, Michael Atiyah, guanyador de la Medalla Fields (1966), va presentar una demostració per contradicció de la hipòtesi de Riemann en el Heidelberg Laureate Forum 2018 (Alemània).[6] Tanmateix, la demostració no es va considerar vàlida en fer suposicions que no eren correctes.[7]
Hipòtesi de Riemann i nombres primers[modifica]
La formulació tradicional de la hipòtesi de Riemann amaga una mica l'autèntica importància de la conjectura. La funció zeta de Riemann té una profunda connexió amb els nombres primers. Helge von Koch va demostrar l'any 1901 que la hipòtesi de Riemann és equivalent al considerable refinament del teorema dels nombres primers: Existeix una constant C > 0 tal que
per tot x suficientment gran, on π(x) és la funció comptadora de nombres primers i ln(x) és el logaritme natural de x. Lowell Schoenfeld va demostrar que es pot prendre C = 1/(8 π) per tot x ≥ 2657.
Els zeros de la funció zeta i els nombres primers satisfan certes propietats de dualitat, conegudes com fórmules explícites, que mostren, utilitzant l'anàlisi de Fourier, que es poden interpretar els zeros de la funció zeta de Riemann com freqüències harmòniques en la distribució dels nombres primers.
Encara més, si la conjectura de Hilbert-Polya és certa, llavors qualsevol operador que dongui les parts imaginàries dels zeros com els seus valors propis ha de satisfer:
on tr és la traça de l'operador (suma dels seus valors propis), és un nombre imaginari i és la funció de Txebixov que suma el log(x) en el conjunt dels primers i les seves potències enteres. Aquesta fórmula és una conclusió de la 'fórmula explícita' de V. Mangoldt.[8] Diversos operadors proposats per Carlos Castro Perelman, J. Macheca y J. García, semblen corroborar els resultats de la conjectura de Hilbert sobre l'operador, reproduint la part imaginària dels zeros.
Càlcul numèric[modifica]

- L'any 2004 Xavier Gourdon va verificar la conjectura de Riemann numèricament al llarg dels primers deu trilions de zeros no trivials de la funció. No obstant això, no és estrictament una demostració, numèricament és més interessant de trobar un contra-exemple, és a dir un valor de zero que no compleixi que la seva part real sigui igual a 1/2, ja que això faria saltar pels aires la validesa de la conjectura.
- Fins al 2005, l'intent més serió d'explorar els zeros de la funció-ζ, és el ZetaGrid, un projecte de computació distribuïda amb la capacitat de verificar milions de zeros al dia. El projecte va acabar el desembre de 2005, i cap dels zeros va poder ser identificat com a contra-exemple de la hipòtesi de Riemann.
Repercussions[modifica]
La hipòtesi de Riemann afirma que tots els altres zeros no trivials de la funció (zeta) es troben en la recta vertical que passa per , és a dir, són nombres complexos de la forma , .
Aquesta funció té una profunda connexió amb els nombres primers on els zeros de la funció zeta i els nombres primers satisfan certes propietats de dualitat, conegudes com a fórmules explícites, que mostren, utilitzant anàlisi de Fourier, que aquests zeros poden interpretar-se com freqüències harmòniques en la distribució dels nombres primers.
Coneixent la relació dels nombres primers amb la funció , algunes de les repercussions que va tenir aquesta funció són les següents
- Estimadors precisos del terme quocient del teorema dels nombres primers:
Hege von Koch va demostrar que la hipòtesi de Riemann és equivalent al teorema dels nombres primeres que enuncia que:
Existeix una constant C tal que:
|
- Comparació de i Li(x):
Per a valros de x petits s'havia demostrat que , fet que va fer que es conjecturés que Li(x) era una cota superior estricta de i que per tant l'equació no té solucions reals.
No obstant això, l'any 1914 Littlewood va usar la hipòtesi de Riemann per mostrar que la desigualtat s'inverteix per valors suficientment grans de x.
L'any 1933, Skewes va utilitzar la hipòtesi de Reimann per demostrar que la desigualtat s'inverteix per a alguns i l'any 1955, sense utilitzar la hipòtesi, va mostrar que la desigualtat s'inverteix per a alguns
- Les distàncies entre els nombres primers consecutius:
Cramer va demostrar que la hipòtesi de Riemann implica que existeix una constant on és el k-èssim nombre primer. Existeix un resultat millor que el de Cramér, que afirma que[9]
on pn denota l'n-èssim nombre primer i "log" denota el logaritme natural.
Referències[modifica]
- ↑ Bombieri, Enrico (2000), The Riemann Hypothesis - official problem description, Clay Mathematics Institute, <http://www.claymath.org/millennium/Riemann_Hypothesis/riemann.pdf>. Consulta: 21 febrer 2011 Reimprès a (Borwein et al. 2008)
- ↑ «El problema cuya solución quizás la conozcan en el cielo» (en castellà). NAUKAS. [Consulta: 11 agost 2022].
- ↑ «The Millennium Prize Problems» (en anglès). Arxivat de l'original el 8 de gener de 2008. [Consulta: 21 febrer 2011].
- ↑ Weisstein, Eric W. «Riemann Hypothesis» (en anglès). [Consulta: 27 agost 2021].
- ↑ Riemann, Bertrand. «Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse» (en anglès), 1859. [Consulta: 29 desembre 2008].
- ↑
 Hipòtesi de Riemann a YouTube
Hipòtesi de Riemann a YouTube
- ↑ #author.fullName}. «Riemann hypothesis likely remains unsolved despite claimed proof» (en anglès americà). [Consulta: 18 maig 2022].
- ↑ Explicit formula http://www.wbabin.net/science/moreta8.pdf Arxivat 2010-06-19 a Wayback Machine.
- ↑ Cramér, Harald «On the order of magnitude of the difference between consecutive prime numbers». Acta Arithmetica, 2, 1936, p. 23–46. Arxivat de l'original el 2018-07-23 [Consulta: 12 març 2012].






![{\displaystyle \sum _{n}e^{-\beta E_{n}}=\operatorname {tr} [e^{-\beta {\hat {H}}}]=e^{u/2}-e^{-u/2}{\frac {d\psi _{0}}{du}}-{\frac {e^{u/2}}{e^{3u}-e^{u}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89764162348181454cda8b451b58cf0066636006)







![{\displaystyle \forall x:\pi (x)=card[p\geq 2,primo,p\leq x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9c8f935204058a4e5d923df52d99e0f1b16072b)








