Pertorbació (astronomia)
|
|
Aquest article o secció necessita millorar una traducció deficient. en |
En astronomia, una pertorbació és el moviment complex d'un cos massiu que depèn de forces diferents a l'atracció gravitatòria d'un altre cos massiu.[1] Les altres forces poden incloure un tercer cos (quart, cinquè, etc.), la resistència, a partir d'una atmosfera, i l'atracció fora del centre d'un cos aplatat o d'una altra manera deformat.[2]

Introducció[modifica]
L'estudi de les pertorbacions comencen amb els primers intents de predir els moviments planetaris del cel, tot i que en l'antiguitat les causes n'eren un misteri. Newton, en el moment de formular les seves lleis de moviment i de la gravitació, les va aplicar a la primera anàlisi de les pertorbacions,[2] reconeixent les complexes dificultats del seu càlcul.[3] Molts dels grans matemàtics, des de llavors, han prestat atenció als diversos problemes que comporta; al llarg dels segles xviii i xix hi va haver demanda de taules precises de la posició de la Lluna i els planetes per a la navegació marina.
Es poden dividir els moviments complexos de les pertorbacions gravitacionals. El moviment hipotètic que el cos segueix sota l'efecte gravitacional d'un altre cos només és típicament una secció cònica, i es pot descriure fàcilment amb els mètodes de la geometria. S'anomena problema dels dos cossos, o òrbita kepleriana no pertorbada. Les diferències entre aquest i el moviment real del cos són pertorbacions a causa dels efectes gravitacionals addicionals del cos o cossos restants. Si només hi ha un altre cos significatiu, el moviment pertorbat és un problema dels tres cossos; si hi ha diversos altres cossos, és un problema dels n cossos. Hi ha una solució analítica general (una expressió matemàtica per predir les posicions i moviments en qualsevol moment futur) per al problema dels dos cossos; quan es consideren però, més de dos cossos només hi ha solucions analítiques per a casos especials. Fins i tot el problema dels dos cossos es torna insoluble si un dels cossos té forma irregular.[4]

La majoria dels sistemes que impliquen múltiples atraccions gravitacionals presenten un cos primari dominant en els seus efectes (per exemple, una estrella, en el cas de l'estrella i el seu planeta, o un planeta, en el cas del planeta i el seu satèl·lit). Els efectes gravitacionals dels altres cossos es poden tractar com pertorbacions de l'hipotètic moviment no positiu del planeta o satèl·lit al voltant del seu cos primari.
Anàlisi matemàtica[modifica]
Pertorbacions generals[modifica]
En els mètodes de pertorbacions generals, les equacions diferencials generals, ja siguin de moviment o de canvi en els elements orbitals, generalment es resolen analíticament pel desenvolupament en sèrie. El resultat se sol expressar en termes de funcions algebraiques i trigonomètriques dels elements orbitals del cos en qüestió i dels cossos pertorbadors. Això es pot aplicar a molts conjunts de condicions diferents, i no és específic per a cap conjunt determinat d'objectes gravitadors.[5]
Històricament, primer es van investigar les pertorbacions generals. Els mètodes clàssics es coneixen com a variació dels elements, variació dels paràmetres o variació de les constants d'integració. En aquests mètodes, es considera que el cos sempre es mou en una secció cònica, però la secció cònica està canviant constantment a causa de les pertorbacions. Si totes les pertorbacions cessessin en qualsevol moment particular, el cos continuaria en aquesta secció cònica (actualment inamovible) indefinidament; i és coneguda com a òrbita osculatriu i els seus elements orbitals en un moment determinat són els que es busquen pels mètodes de pertorbacions generals.[2]
Les pertorbacions generals aprofiten el fet que, en molts problemes de la mecànica celeste, l'òrbita de dos cossos canvia lentament a causa de les pertorbacions: l'òrbita de dos cossos és una bona primera aproximació. Les pertorbacions generals només són aplicables si les forces pertorbadores tenen un ordre de magnitud menor, o menor que la força gravitacional del cos primari.[4] En el Sistema solar, aquest sol ser el cas de Júpiter, el segon cos més gran, que té una massa al voltant d'1/1.000 la del Sol.
Els mètodes de pertorbació general són preferits per a alguns tipus de problemes, ja que la font de certs moviments observats es troba fàcilment. Això no ocorre necessàriament per a les pertorbacions especials; els moviments es prediuen amb precisió semblant, però no hi ha informació sobre les configuracions dels cossos pertorbadors (com ara, una ressonància orbital) que els provocaria.[4]
Pertorbacions especials[modifica]
En els mètodes de pertorbacions especials, els conjunts de dades numèriques, que representen els valors de les posicions, velocitats i forces acceleradores dels cossos d'interès, són la base de la integració numèrica de les equacions diferencials del moviment.[6] En efecte, les posicions i velocitats són pertorbades directament, i no es fa cap intent de calcular les corbes de les òrbites o dels elements orbitals.[2] Les pertorbacions especials es poden aplicar a qualsevol problema de mecànica celeste, ja que no es limita als casos en què les forces pertorbadores són petites.[4] Una vegada aplicats només als cometes i als planetes menors, els mètodes de pertorbació especials són ara la base de les efemèrides planetàries més precises dels grans anuaris astronòmics.[7] Les pertorbacions especials també s'utilitzen per al modelatge d'una òrbita amb l'ajut d'ordinadors.
Mètode de Cowell[modifica]
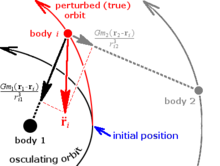
El mètode de Cowell (anomenat així per Philip H. Cowell, que, amb A. C. D. Cromellin, utilitza un mètode similar per predir el retorn del cometa de Halley) és potser el més simple dels mètodes especials de pertorbació.[8] En un sistema de cossos que interaccionen mútuament, aquest mètode resol matemàticament la llei de la gravitació universal de Newton en el cos sumant les interaccions individuals dels altres cossos:
en què és el vector d'acceleració del cos , és la constant gravitacional, és la massa del cos , i són els vectors de posició d'objectes i respectivament, i és la distància des de l'objecte a l'objecte . Tots els vectors es refereixen al baricentre del sistema. Aquesta equació es resol en components en , , i i aquests estan integrats numèricament per formar els nous vectors de velocitat i posició. Aquest procés es repeteix tantes vegades com sigui necessari. L'avantatge del mètode de Cowell és la facilitat d'aplicació i programació. Un desavantatge n'és que quan les pertorbacions esdevenen grans en magnitud (com quan un objecte fa un apropament a un altre) els errors del mètode també es fan grans.[9] Tanmateix, per a molts problemes de mecànica celeste, aquest no és mai el cas. Un altre desavantatge és que en sistemes amb un cos central dominant, com el Sol, cal portar molts dígits significatius en aritmètica a causa de la gran diferència en les forces del cos central i els cossos pertorbadors, tot i que amb ordinadors moderns això no és gairebé la limitació que tenia antigament.[10]
El mètode d'Encke[modifica]

El mètode d'Encke comença amb l'òrbita osculatriu com a referència i s'integra de manera numèrica per resoldre la variació de la referència en funció del temps.[11]
Els seus avantatges són que les pertorbacions són generalment petites, de manera que la integració pot procedir en passos més grans (amb errors resultants menors), i el mètode no és tan afectat per les pertorbacions extremes. El seu desavantatge rau en la complexitat, no es pot utilitzar indefinidament sense l'actualització ocasional de l'òrbita osculatriu i continuar des d'allà, un procés conegut com a rectificació.[9] El mètode d'Encke és semblant al mètode de pertorbació general de la variació dels elements, excepte que la rectificació es realitza a intervals discrets en comptes de contínuament.[12]
Deixar que sigui el vector de radi de l'òrbita osculatriu, el vector de radi de l'òrbita pertorbada, i la variació de l'òrbita osculatriu,
-
, i l'equació de moviment de simplement és
()
-
.
()
i són només les equacions de moviment de i ,
-
per l'òrbita pertorbada i
()
-
per l'òrbita no pertorbada,
()
en què és el paràmetre gravitacional amb i les masses del cos central i el grup pertorbat, és l'acceleració pertorbadora, i i són les magnituds de i .
Substituint les equacions (3) i (4) en l'equació (2),
-
,
()
que, en teoria, es podria integrar dues vegades per trobar . Des de l'òrbita osculatriu fàcilment es pot calcular mitjançant dos mètodes de cos, i es comptabilitzen i es pot resoldre. En la pràctica, la quantitat entre els claudàtors, , és la diferència de dos vectors gairebé iguals, i cal una manipulació addicional per evitar la necessitat d'obtenir dígits addicionals significatius.[13][14] El mètode d'Encke es va utilitzar amb més freqüència abans de l'aparició dels ordinadors moderns, quan gran part del càlcul orbital es realitzava en calculadores mecàniques.
Naturalesa periòdica[modifica]

En el Sistema solar, moltes de les pertorbacions d'un planeta per si mateixes són periòdiques, i consisteixen en petits impulsos cada vegada que un planeta passa per un altre en la seva òrbita. Això fa que els cossos segueixin moviments periòdics o quasi periòdics, com la Lluna en la seva òrbita fortament pertorbada, que és el subjecte de la teoria lunar. Aquesta naturalesa periòdica dugué al descobriment de Neptú el 1846, conseqüència de les seves pertorbacions de l'òrbita d'Urà.
Les pertorbacions recíproques de planetes causen variacions quasi periòdiques a llarg termini en els seus elements orbitals, la majoria de les quals són evidents quan els períodes orbitals de dos planetes estan gairebé en sincronia. Per exemple, cinc òrbites de Júpiter (59,31 anys) són gairebé iguals a dues de Saturn (58,91 anys). Això provoca grans pertorbacions en tots dos, amb un període de 918 anys, el temps necessari per a la petita diferència en les seves posicions en relació a fer un cercle complet, que Laplace fou el primer a descobrir.[2] Actualment Venus té l'òrbita amb la menor excentricitat, és a dir, és la més propera a la circular de totes les òrbites planetàries. En 25.000 anys, la Terra tindrà una òrbita més circular (menys excèntrica) que la de Venus. S'ha demostrat que les pertorbacions periòdiques a llarg termini dins del Sistema solar poden ocórrer caòticament a través d'escales de temps molt llargues; sota algunes circumstàncies, un o més planetes poden creuar l'òrbita de l'altre, donant lloc a col·lisions.[15]
Les òrbites de molts dels cossos menors del Sistema solar, com els cometes, sovint estan molt pertorbades, particularment pels camps gravitacionals dels gegants gasosos. Encara que moltes d'aquestes pertorbacions són periòdiques, altres no ho són, i aquestes en particular poden representar aspectes del moviment caòtic. Per exemple, a l'abril del 1996, la influència gravitatòria de Júpiter va fer que el període orbital del cometa Hale-Bopp disminuís de 4.206 a 2.380 anys, un canvi que no es tornaria a produir periòdicament.[16]
Referències[modifica]
- ↑ Bate, Roger R.; Mueller, Donald D.; White, Jerry E. Fundamentals of Astrodynamics. Dover Publications, Inc., New York, 1971. ISBN 0-486-60061-0., e.g. at ch. 9, p. 385.
- ↑ 2,0 2,1 2,2 2,3 2,4 Moulton, Forest Ray. «An Introduction to Celestial Mechanics, Second Revised Edition», 1914. chapter IX. (a Google books).
- ↑ El 1684, Newton va escriure: "A causa de la desviació del Sol del centre de gravetat, la força centrípeta no sempre tendeix a aquest centre immòbil i, per tant, els planetes no es mouen exactament en el·lipses ni giren dues vegades en la mateixa òrbita. Cada vegada que un planeta gira traça una òrbita nova, com en el moviment de la Lluna, i cada òrbita depèn dels moviments combinats de tots els planetes, per no parlar de l'acció dels uns sobre els altres, però considerar simultàniament totes aquestes causes del moviment i definir aquests moviments per lleis exactes que admeten un càlcul fàcil superen, si no m'equivoco, la força de qualsevol ment humana". (Citat pel professor G. E. Smith (Universitat de Tufts), en in "Three Lectures on the Role of Theory in Science". Arxivat 2005-03-10 a Wayback Machine.
- ↑ 4,0 4,1 4,2 4,3 Roy, A.E.. Orbital Motion. third. Institute of Physics Publishing, 1988. ISBN 0-85274-229-0., chapters 6 and 7.
- ↑ Bate, Mueller, White (1971), e.g. at p.387 and at section 9.4.3, p.410.
- ↑ Bat, Mueller, White (1971), pàgs. 387-409.
- ↑ See, for instance, Jet Propulsion Laboratory Development Ephemeris.
- ↑ Brouwer, Dirk; Clemence, Gerald M. Methods of Celestial Mechanics. Academic Press, New York and London, 1961., p. 186.
- ↑ 9,0 9,1 Danby, J.M.A.. Fundamentals of Celestial Mechanics. second. Willmann-Bell, Inc., 1988. ISBN 0-943396-20-4., chapter 11.
- ↑ Herget, Paul. The Computation of Orbits. privately published by the author, 1948., p. 91 ff.
- ↑ Anomenat així per Johann Franz Encke; Battin, Richard H. An Introduction to the Mathematics and Methods of Astrodynamics, Revised Edition. American Institute of Aeronautics and Astronautics, Inc., 1999. ISBN 1-56347-342-9., p. 448.
- ↑ Battin (1999), sec. 10.2.
- ↑ Bate, Mueller, White (1971), sec. 9.3.
- ↑ Roy (1988), sec. 7.4.
- ↑ Vegeu referències a l'estabilitat del Sistema solar.
- ↑ Don Yeomans. «Comet Hale–Bopp Orbit and Ephemeris Information». JPL/NASA, 10-04-1997. [Consulta: 23 octubre 2008].
Bibliografia[modifica]
- Bate, Roger R.; Mueller, Donald D.; White, Jerry E. Fundamentals of Astrodynamics. Nova York: Dover Publications, 1971. ISBN 0-486-60061-0.
- Moulton, Forest Ray. An Introduction to Celestial Mechanics. 2nd revised, 1914.
- Roy, A. E.. Orbital Motion. 3rd. Institute of Physics Publishing, 1988. ISBN 0-85274-229-0.
Vegeu també[modifica]
- Nereida, una de les llunes exteriors de Neptú amb una alta excentricitat orbital de ~ 0,75 i és sovint pertorbada.
- Òrbita osculatriu
- Ressonància orbital
- Estabilitat del sistema solar
- Formació i evolució del sistema solar
Enllaços externs[modifica]
- Solex (per Aldo Vitagliano): prediccions per a la posició / òrbita / acostaments de Mart (anglès).
- Gravitation. Sir George Biddell Airy's 1884 book on gravitational motion and perturbations, using little or no math. A good source if you can stand the flowery 19th-century English (en Google books) (anglès).






























