Paral·lelogram
 | |
| Tipus | paral·lelògon, paral·lelòtop, zonogon (en) |
|---|---|
| Forma de les cares | aresta (4) |
| Més informació | |
| MathWorld | Parallelogram |
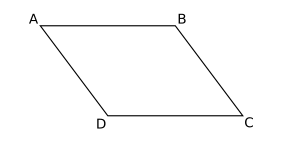
En geometria, un paral·lelogram és un quadrilàter els costats oposats del qual són paral·lels. Un paral·lelogram és un cas particular de trapezi. Si els angles d'un paral·lelogram són iguals (en conseqüència, són angles rectes) llavors també és un rectangle. Però si els costats d'un paral·lelogram són d'igual longitud llavors també és un rombe. En canvi si els angles d'un paral·lelogram són iguals i els costats són d'igual longitud llavors també és un quadrat, o si els costats oposats d'un paral·lelogram són d'igual longitud. Els angles de vèrtexs oposats d'un paral·lelogram són iguals. Els angles adjacents d'un paral·lelogram són suplementaris i les diagonals d'un paral·lelogram s'intersecten al seu punt mitjà.
Fórmules de mesura[modifica]
L'àrea d'un paral·lelogram es pot calcular a partir de les longituds de la base i de l'altura i val:
El perímetre d'un paral·lelogram de costat de longituds i val:
Casos especials[modifica]

- Romboide – Un paral·lelogram en què els costats adjacents són desiguals i els seus angles no són rectes.[1]
- Rectangle – Un paral·lelogram amb els quatre angles rectes, i costats iguals dos a dos.[2]
- Rombe – Un paral·lelogram amb els quatre costats iguals i els angles iguals dos a dos.
- Quadrat – Un paral·lelogram amb els quatre costats d'igual longitud i els angles iguals (angles rectes).
Caracterització[modifica]
Un quadrilàter simple és un paral·lelogram si i només si qualsevol de les següents afirmacions es compleix:[3][4]
- Les dues parelles de costats oposats són iguals en longitud.
- Les dues parelles d'angles són iguals en mesura.
- Les dues diagonals es biseccionen mútuament.
- Dos costats oposats són paral·lels i iguals en longitud.
- Els angles adjacents són suplementaris.
- Cada diagonal divideix el quadrilàter en dos triangles congruents.
- La suma dels quadrats dels costats és igual a la suma dels quadrats de les diagonals (això és la llei del paral·lelogram).
- Té simetria rotacional d'ordre 2.
- La suma de les distàncies de qualsevol punt interior als costats és independent a la ubiació del punt.[5] (això és una extensió del teorema de Viviani).
Per tant, tots el paral·lelograms tenen totes les propietats llistades, i vice-versa, si només una de les afirmacions és certa en un quadrilàter simple, llavors és aquest quadrilàter és un paral·lelogram.
Referències[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Paral·lelogram |
- ↑ Nuñez, Pedro. Libro de Algebra en Arithmetica y Geometria, 1567. «Romboide es figura cuadrilátera, en la cual solamente los lados opósitos son iguales, y los ángulos no son rectos, y en esto es diferente del cuadrángulo rectángulo, que no es cuadrado»
- ↑ «Rectangle» (en anglès). Wolfram Mathworld. Eric Weisstein. [Consulta: 24 gener 2017].
- ↑ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, pp. 51-52.
- ↑ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, p. 22.
- ↑ Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.





