Patró de moaré
En matemàtiques, física i art, un patró de moaré[1] són uns patrons d'interferència a gran escala que es poden produir quan es sobreposa un patró reglat opac amb buits transparents sobre un altre patró similar.[2] Perquè aparegui el patró d'interferència de moaré, els dos patrons no han de ser completament idèntics, sinó més aviat desplaçats, girats o amb un to lleugerament diferent.
-
Efecte de moaré quan se superposen dos patrons de punts del mateix to però desplaçats
Les línies poden ser les fibres d'un teixit de moaré (les que donen el nom a l'efecte), o bé senzilles línies en una pantalla d'ordinador, l'efecte es presenta igualment en els dos casos. El sistema visual humà crea la il·lusió de bandes fosques i clares horitzontals, que se superposen a les línies fines que en realitat són les que formen la traça.
-
Móvil, Eusebio Sempere, 1972; escultura a l'aire lliure explotant l'efecte de moaré (Madrid)
-
Patró de moaré que apareix a les captures de pantalla LCD
-
Detall d'un micròmetre
Els patrons de moaré apareixen en moltes situacions. A la impressió, el patró imprès de punts pot interferir amb la imatge. A la televisió i la fotografia digital, un patró d'un objecte fotografiat pot interferir amb la forma dels sensors de llum per generar artefactes no desitjats. De vegades també es creen deliberadament: en micròmetres s’utilitzen per amplificar els efectes de moviments molt petits. També es poden formar patrons de moaré més complexos en superposar figures complexes fetes de línies corbes i entrellaçades.[3]
-
Les línies fines que formen el cel en aquesta imatge creen patrons de moaré quan es mostren en algunes resolucions per la mateixa raó que les fotografies de televisors presenten patrons de moaré: les línies no són absolutament planes
-
Patró de moaré clarament visible en aquesta fotografia de les plomes d'un lloro (més pronunciada a la imatge a mida completa)
-
Patró de moaré vist sobre una gàbia al zoo de San Francisco
-
Patró de moaré vist en un rellotge digital
Els patrons de moaré poden arribar a ser considerats artefactes en el context dels gràfics per computadors i la infografia, ja que poden incloure's durant el procés de captura d'una imatge digital (per exemple, durant l'escaneig d'una imatge amb detalls molt fins) o produir-se durant la generació d'una imatge sintètica en 3D.
-
La diferència de distància de la barana davantera i posterior d'un pont crea patrons de moaré
-
En aquesta fotografia es pot veure el patró de moaré a la porta metàl·lica del garatge
En física, la seva manifestació és la interferència d'ones com la que es veu a l'experiment de la doble escletxa i el fenomen del bategament en acústica.
Els patrons de moaré també poden ser útils en el context de l'estudi de la fatiga de materials. Una reixa obtinguda d'un material intacte pot superposar-se a una reixa obtinguda del mateix material sota esforços, i gràcies als patrons de moaré els canvis diminuts en el material poden fer-se aparents, puix que el patró de moaré és molt més visible que les diferències elàstiques del material.
Etimologia[modifica]
El terme s’origina a partir de la paraula francesa moiré (pronunciat [mwaˈʀe]), un tipus de tèxtil, tradicionalment de seda però ara també de cotó o fibra sintètica, amb un aspecte ondulat o «regat». El moaré, o «tèxtil regat», es fa prement dues capes del tèxtil quan està mullat. L'espaiat similar però imperfecte dels fils crea un patró característic que queda després que la tela s'assequi.[4]
-
Teixit de moaré
En francès, l'adjectiu moiré (en ús des d'almenys 1823) deriva del verb moirer anterior, «produir un teixit regat teixint o premsant». Moirer, al seu torn, és una variació de la paraula mouaire que és una adopció de l'anglès mohair (en ús des d'almenys 1570). Mohair prové de l'àrab mukhayyar (مُخَيَّر, lit. «escollit»), un drap fet amb la llana de la cabra d'Angora. Mukhayyar (مُخَيَّر) prové de la paraula khayyara (خيّر, lit. «ell tria»), que s'entén en el sentit «d'una tela triada o excel·lent».[5]
La formació del patró de moaré[modifica]
Els patrons de moaré solen ser un artefacte d'imatges produïdes per diverses tècniques d'imatge digital i gràfics per ordinador, per exemple quan s’escaneja una imatge de semitons o un traçat de raigs d'un pla a quadres (aquest darrer és un cas especial d'aliàsing, a causa de la subestacionària d'un patró regular fi).[6] Això es pot superar en el mapatge de textures mitjançant l'ús de mapes MIP i filtratge anisotròpic.
Les línies podrien representar fibres de seda moaré o línies dibuixades sobre paper o sobre una pantalla d'ordinador. La interacció no lineal dels patrons òptics de línies crea un patró real i visible de bandes fosques i clares aproximadament paral·leles, el patró moaré, superposat a les línies.[7]
L'efecte moaré també es produeix entre objectes transparents superposats.[8] Per exemple, una màscara de fase invisible està formada per un polímer transparent amb un perfil de gruix ondulat. A mesura que la llum brilla a través de dues màscares superposades de patrons de fase similars, es produeix un ampli patró moaré en una pantalla a certa distància. Aquest efecte moaré de fase i l'efecte clàssic moaré de línies opaques són dos extrems d'un espectre continu en òptica, que s’anomena efecte moaré universal.
-
Línia de moaré amb un moviment lent de la capa reveladora cap amunt
-
Patró de moaré creat mitjançant la superposició de dos conjunts de cercles concèntrics
-
Figura de moaré
-
Corbes de moaré modificant els patrons de les capes
L'efecte moaré de fase és la base d'un tipus d'interferòmetre de banda ampla en aplicacions de raigs X i ones de partícules. També proporciona una manera de revelar patrons ocults en capes invisibles.
Línia de moaré[modifica]
La línia de moaré és un tipus de patró de moaré; un patró que apareix quan se superposen dues capes transparents que contenen patrons opacs correlacionats. La línia de moaré és el cas quan els patrons superposats comprenen línies rectes o corbes. En moure els patrons de capa, els patrons de moaré es transformen o es mouen a una velocitat més ràpida. Aquest efecte s’anomena acceleració òptica de moaré.
Es creen patrons de línia de moaré més complexos si les línies són corbes o no són exactament paral·leles.
Figura de moaré[modifica]
La figura de moaré és un tipus de patró de moaré que demostra el fenomen de l'augment de moaré.[9][10] La figura de moaré 1D és el cas particular simplificat de la figura de moaré 2D. Poden aparèixer patrons unidimensionals quan se superposa una capa opaca que conté minúscules línies transparents horitzontals a sobre d'una capa que conté una forma complexa que es repeteix periòdicament al llarg de l'eix vertical.
Els patrons de moaré que revelen figures complexes o seqüències de símbols incrustats en una de les capes (en forma de formes comprimides repetides periòdicament) es creen amb figures de moaré, també anomenades patrons de bandes de moaré. Una de les propietats més importants de la figura de moaré és la seva capacitat per augmentar petites formes al llarg d'un o dels dos eixos, és a dir, d'estirar-se. Un exemple 2D comú d'augment de moaré es produeix quan es visualitza una tela metàl·lica a través d'una segona tela metàl·lica de disseny idèntic. La fina estructura del disseny és visible fins i tot a grans distàncies.
Reducció del patró de moaré[modifica]

És possible reduir el patró de moaré aplicant filtres o amb alguns trucs. En el cas d'una digitalització d'un document, es pot limitar el patró de moaré girant la imatge. Com que l'escaneig ja no es fa en els mateixos eixos, el patró es pot reduir o amplificar. El filtratge amb un filtre gaussià limita el patró de moaré sense erradicar-lo del tot. S’obtenen resultats similars amb un filtre mitjà.
Sovint, els controladors d'escàner tenen una opció per eliminar el patró de moaré. Els algoritmes poden ser més o menys avançats, però, en general, el mètode habitual consisteix a ampliar la imatge mitjançant una interpolació i aplicar un desenfocament gaussià en aquesta versió sobremostrada. A continuació, es pot reduir la mida de la imatge perquè les dimensions coincideixin amb l'original. Es pot aplicar un filtre de tipus «accentuació» per a ressaltar els detalls.
Un filtrat més avançat aprofita el fet que el patró de moaré té una certa freqüència amb un predomini general en un eix concret. Amb els filtres de pas de banda, és possible eliminar de l'espectre les freqüències relacionades amb el patró de moaré.
Tanmateix, aquest problema continua sent difícil a la pràctica perquè el fenomen és sovint no lineal (imatges procedents d'un sistema analògic) o pertorbat pel soroll.
Càlculs[modifica]
Patrons de moaré paral·lels[modifica]
Enfocament geomètric[modifica]
Sigui dos patrons fets de línies paral·leles i equidistants, per exemple, línies verticals. La distància entre línies del primer patró és p, la distància entre línies del segon patró és p + δp, amb 0 < δp < p.
Si les línies dels patrons se superposen a l'esquerra de la figura, el desplaçament entre les línies augmenta en anar cap a la dreta. Després d'un nombre determinat de línies, els patrons s'oposen: les línies del segon patró es troben entre les línies del primer patró. Si es mira des de molt lluny, es té la sensació de zones pàl·lides quan les línies se superposen (hi ha blanc entre les línies) i de zones fosques quan les línies estan «oposades».
-
Els patrons se superposen a la part mitjana de la figura
-
Moaré obtingut per la superposició de dos patrons similars girats per un angle α
El centre de la primera zona fosca és quan el desplaçament és igual a p2. La n línia del segon patró es desplaçada per n δp en comparació amb la n línia del primer patró. Això correspon a la meitat de la primera zona fosca
- com més gran sigui la distància entre les línies, més gran serà la distància entre les zones pàl·lides i fosques;
- com més gran sigui la discrepància δp, més properes són les zones fosques i pàl·lides; un gran espai entre zones fosques i pàl·lides significa que els patrons tenen les distàncies entre les línies molt petites.
El principi del moaré és similar a l'escala Vernier.
Enfocament amb funcions matemàtiques[modifica]

L'essència de l'efecte de moaré és la percepció (principalment visual) d'un tercer patró clarament diferent que és causat per una superposició inexacta de dos patrons similars. La representació matemàtica d'aquests patrons no s’obté trivialment i pot semblar una mica arbitrària. En aquesta secció donarem un exemple matemàtic de dos patrons paral·lels la superposició dels quals forma un patró de moaré i mostrarem d'una manera (de moltes maneres possibles) que aquests patrons i l'efecte de moaré es puguin representar matemàticament.
La visibilitat d'aquests patrons depèn del suport o substrat en què apareixen, i poden ser opacs (com per exemple en paper) o transparents (com per exemple en una pel·lícula de plàstic). A efectes de discussió, assumirem que els dos patrons principals s’imprimeixen amb tinta en escala de grisos sobre un full blanc, on l'opacitat (per exemple, tonalitat de gris) de la part «impresa» ve donada per un valor entre 0 (blanc) i 1 (negre) inclòs, amb 12 que representa el gris neutre. Qualsevol valor inferior a 0 o superior a 1 que utilitzi aquesta escala de grisos és essencialment «no imprimible».
També escollirem representar l'opacitat del patró resultant d'imprimir un patró damunt l'altre en un punt determinat del paper com a mitjana (és a dir, la mitjana aritmètica) de l'opacitat de cada patró en aquesta posició, que és la meitat de la seva suma, i, tal com es calcula, no supera 1 (aquesta opció no és única. Qualsevol altre mètode per combinar les funcions que satisfaci mantenir el valor de la funció resultant dins dels límits [0,1] també servirà; la mitjana aritmètica té la virtut de la simplicitat, amb un mínim dany possible als conceptes del procés de gravació).
Ara considerem la «impressió» de la superposició de dos patrons a escala de grisos gairebé similars, que varien sinusoidalment, per mostrar com produeixen un efecte moaré en imprimir primer un patró al paper i després imprimir l'altre patró sobre el primer, mantenint el seu eix de coordenades en registre. Representem la intensitat de gris de cada patró per una funció d'opacitat positiva de distància al llarg d'una direcció fixa (per exemple, la coordenada x) en el pla de paper, en la forma
on la presència d'1 manté la funció positiva definida i la divisió per 2 impedeix valors de funció superiors a 1.
La quantitat k representa la variació periòdica (és a dir, freqüència espacial) de la intensitat de gris del patró, mesurada com el nombre de cicles d'intensitat per unitat de distància. Atès que la funció sinus és cíclica per sobre dels canvis d'arguments de 2π, l'increment de la distància Δx per cicle d'intensitat (la longitud d'ona) s'obté quan k Δx = 2π, o Δx = 2πk.
Considerem ara en aquests dos patrons, en què un té una variació periòdica lleugerament diferent de l'altre:
de tal manera que k1 ≈ k₂.
La mitjana d'aquestes dues funcions, que representa la imatge impresa superposada, s’avalua de la següent manera:
on es demostra fàcilment que
i
Aquesta funció mitjana, f₃, es troba clarament en el rang [0,1]. Des de la variació periòdica A és la mitjana i, per tant, propera a k1 i k₂, l'efecte de moaré es demostra de manera distintiva mitjançant la funció de «batec» de l'envolupant sinusoidal de cos(Bx), la variació periòdica de la qual és la meitat de la diferència de les variacions periòdiques k1 i k₂ (i, evidentment, molt inferior en freqüència).
Altres efectes moaré unidimensionals inclouen el clàssic bategament del to de freqüència que s’escolta quan sonen simultàniament dues notes pures de to gairebé idèntic. Es tracta d'una versió acústica de l'efecte de moaré en l'única dimensió del temps: les dues notes originals segueixen presents, però la percepció de l'oient és de dos tons que són la diferència de la mitjana de les freqüències de les dues notes. L'aliàsing en el mostreig de senyals que varien en el temps també pertany a aquest paradigma de moaré.
Enfocament sinusoidal[modifica]
Si ja no considerem patrons de línies d'alt contrast, sinó patrons transparents amb un contrast que varien contínuament de manera sinusoide
(els passos són respectivament p1 = 1/k1 i p₂ = 1/k₂), la intensitat quan se superposen els dos patrons és llavors
o bé, segons la fórmula de la suma de dos sinus derivats de les fórmules d'Euler:
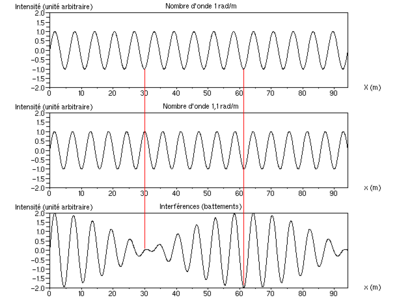
-
Bategaments d'interferència segons la ubicació en un moment determinat, amb una diferència de nombre d'ona de l'1%
-
Superposició de dos patrons amb densitat de gris sinusoidal de longitud d'ona lleugerament diferent
Per tant, es pot veure que la intensitat resultant es compon d'un sinusoide que té una «freqüència espacial» elevada (nombre d'ona) que és la mitjana de les freqüències espacials dels dos patrons i d'un sinusoide amb una freqüència espacial baixa que és la meitat de la diferència en les freqüències espacials dels dos patrons. Aquest segon component és un «embolcall» per a l'altre sinusoide. La longitud d'ona λ d'aquest component és la inversa de la freqüència espacial
ja sigui si el fiquem p1 = p i p₂ = p+δp :
- .
Els zeros d'aquest embolcall estan espaiats λ/2, i els màxims d'amplitud en valor absolut estan igualment espaiats λ/2; per tant, trobem el resultat de l'enfocament clàssic.
Aquest fenomen és similar a l'estroboscòpia temporal o la producció de bategament sonors.
Rotació de patrons[modifica]
Considerem dos patrons amb la mateixa distància entre línies p, però el segon patró gira un angle α. Vist de lluny, també podem veure línies més fosques i clares: les línies clares corresponen a les línies de nodes, és a dir, línies que passen per les interseccions dels dos patrons.
Si considerem una cel·la de la xarxa formada, podem veure que es tracta d'un rombe amb els quatre costats iguals a d = psin α; (tenim un triangle rectangle la hipotenusa del qual és d i el costat oposat a l'angle α és p).
-
Cel·la unitat de la «xarxa»; «ligne claire» significa «línia clara»
-
Efecte del canvi d'angle
Les línies clares corresponen a la petita diagonal del rombe. Com que les diagonals són les bisectrius dels costats veïns, podem veure que la línia pàl·lida fa un angle igual a α2 amb la perpendicular de la línia de cada patró.
A més, l'espai entre dues línies clares és D, la meitat de la diagonal llarga. La diagonal llarga 2D és la hipotenusa d'un triangle rectangle i els costats de l'angle recte són d(1 + cos α) i p. El teorema de Pitàgores dona:
Quan α és molt petit (α < π6) es poden fer les següents aproximacions per a angles petits:
Podem veure que com més petit sigui α, és a dir, com més allunyades són les línies clares; quan els dos patrons són paral·lels (α = 0), l'espai entre les línies clares és infinit (no hi ha cap línia clara).
Per tant, hi ha dues maneres de determinar α: per l'orientació de les línies clares i per la seva separació
Implicacions i aplicacions[modifica]
Impressió d'imatges a tot color[modifica]
En arts gràfiques i preimpressió, la tecnologia habitual per imprimir imatges a tot color implica la superposició de pantalles de semitons. Es tracta de patrons regulars de punts rectangulars, sovint quatre, impresos en cian, groc, magenta i negre. Alguns patrons de moaré són inevitables, però en circumstàncies favorables el patró és «ajustat»; és a dir, la freqüència espacial del moaré és tan alta que no es nota.
-
x
-
Exemples d'angles de pantalla típics de semitons CMYK
-
Aquest primer pla d'una impressió de semitons que mostra com el magenta a la part superior del groc apareix com a taronja/vermell, i el cian a la part superior del groc apareix com a verd.
A les arts gràfiques, el terme moaré significa un patró de moaré excessivament visible. Part de la preimpressió consisteix en seleccionar angles de pantalla i freqüències de semitons que minimitzen el moaré.
La visibilitat del moaré no és del tot predictible. El mateix conjunt de pantalles pot produir bons resultats amb algunes imatges, però amb moaré visibles amb altres.
Pantalles de televisió i fotografies[modifica]
Els patrons de moaré es veuen habitualment a les pantalles de televisió quan una persona porta una camisa o jaqueta d'un teixit o patró concret, com per exemple una jaqueta de pota de gall. Això es deu a l'exploració entrellaçada de televisors i càmeres que no són de pel·lícula, conegut com a vibració interlínia (interline twitter). A mesura que la persona es mou, el patró moaré es nota bastant. Per aquest motiu, els informatius i altres professionals que apareixen regularment a la televisió reben instruccions d'evitar la roba que pugui causar aquest efecte.
-
Efecte «pinta»
-
Demostració de l'exploració entrellaçada i de l'anomenada vibració interlínia (interline twitter)
Les fotografies d'una pantalla de televisor fetes amb una càmera digital sovint presenten patrons de moaré. Com que tant la pantalla del televisor com la càmera digital utilitzen una tècnica d'escaneig per produir o capturar imatges amb línies d'escaneig horitzontals, els conjunts de línies en conflicte provoquen els patrons de moaré. Per evitar l'efecte, la càmera digital es pot orientar a un angle de 30 graus respecte a la pantalla del televisor.
Moaré digital[modifica]
En la cadena de processament digital d'una imatge, pot aparèixer un patró de moaré a l'etapa de digitalització o en la visualització.
-
Aquest disseny de píxels es troba a les pantalles LCD S-IPS. Es fa servir una forma de > per eixamplar el con de visualització
En el primer cas, el patró de moaré apareix per la interferència entre la trama del sensor (escàner o matriu) i el de l'objecte digitalitzat. En el cas dels sensors de color, també pot generar efectes de colors en una imatge que normalment manca.
En el segon cas, el patró de moaré apareix per la interferència entre la matriu de píxels de la pantalla i la trama de l'objecte mostrat. Aquest problema és similar als efectes d'impressió analògiques de semitons descrits anteriorment.
[modifica]
L'efecte de moaré s'utilitza en balises costaneres anomenades «llums d'Inogon», fabricades per Inogon Licens AB, Suècia, per designar el camí de viatge més segur per als vaixells que es dirigeixen a ports esportius, ports, etc. indica els perills submarins (com ara canonades o cables). L'efecte de moaré crea fletxes que apunten cap a una línia imaginària que marca el perill o la línia de pas segur; a mesura que els navegants passen per sobre de la línia, les fletxes de la balisa semblen convertir-se en bandes verticals abans de tornar a les fletxes que apunten en sentit invers.[11][12][13] Es pot trobar un exemple al Regne Unit, a la riba est de Southampton, davant de la refineria de petroli Fawley (50° 51′ 21.63″ N, 1° 19′ 44.77″ O / 50.8560083°N,1.3291028°OO). Es poden utilitzar balises d'efecte de moaré similars per guiar els mariners fins al punt central d'un pont que s’acosta; quan el vaixell està alineat amb la línia central, es veuen línies verticals.
Els llums d'Inogon es desplegen als aeroports per ajudar els pilots a terra a mantenir-se a la línia central de les pistes de rodatge.[14]
Mesura de la deformació[modifica]

A les indústries de fabricació, aquests patrons s’utilitzen per estudiar la deformació microscòpica en materials: deformant una quadrícula respecte a una quadrícula de referència i mesurant el patró de moaré, es poden deduir els nivells i patrons de tensió. Aquesta tècnica és atractiva perquè l'escala del patró de moaré és molt més gran que la fletxa que la provoca, cosa que facilita la mesura.
L'efecte de moaré es pot utilitzar en la mesura de deformacions: l'operador només ha de dibuixar un patró sobre l'objecte i superposar el patró de referència al patró deformat de l'objecte deformat.
Un efecte similar es pot obtenir mitjançant la superposició d'una imatge hologràfica de l'objecte al propi objecte: l'holograma és el pas de referència i la diferència amb l'objecte són les deformacions, que apareixen com a línies pàl·lides i fosques.
Tracció uniaxial[modifica]
Considerem una part de longitud l sobre la qual es dibuixa una xarxa de passos p, les línies de les quals són perpendiculars a l'eix de tracció.
Sota tensió, la peça té una longitud l·(1+ε), on ε és la deformació (allargament relatiu). El pas de la xarxa esdevé p·(1+ε), d'on s'obté δp = p·ε.
Veiem que l'espai entre dues zones fosques és:
per tant, aquest espai permet determinar la deformació. Tanmateix, la mesura de la distància entre dues zones fosques és imprecisa, a causa de l'amplada d'una àrea. Podem estar satisfets comptant el nombre N de línies fosques que veiem: sobre una longitud l, tenim
és a dir
La precisió és la deformació que separa dues aparicions de línies, és a dir
Cisallament pur[modifica]
En el cas de cisallament pur, n’hi ha prou amb dibuixar una xarxa perpendicular a les forces d'escissió. A continuació, la xarxa de la part deformada es fa girar per l'angle de tall γ respecte a la xarxa de referència (la part no deformada).
Pel que fa a la tensió uniaxial, es pot satisfer comptant el nombre de línies, sempre que γ sigui molt baixa, que la part sigui rectangular i que les forces siguin paral·leles als costats (les línies clares són gairebé paral·leles als costats de la peca).
Si l'amplada de la peça (perpendicular a les forces) és l, el nombre de línies N és igual a:
és a dir
amb l'error de l'anterior
Processament d'imatges[modifica]
Alguns programes d'ordinador d'escàner d'imatges proporcionen un filtre opcional, anomenat filtre «descreen», per eliminar artefactes de patró de moaré que d'una altra manera es produirien en escanejar imatges de semitons impreses per produir imatges digitals.[15]
Mesura de petits desplaçaments[modifica]

Considerem un patró fixat en una part, observat a través d'una retícula amb la distància entre línies lleugerament diferent, considerada fixa. Per tant, tenim un patró de moaré.
A mesura que es mou la peça, també es mouen les línies fosques i clares del patró de moaré; per a un desplaçament de δp, les línies es mouen per p, en la direcció oposada del moviment. Trobem el comportament del vernier. Per tant, tenim un factor d'amplificació de p / δp. Això permet mesurar moviments petits i velocitats baixes.
Bitllets[modifica]
Molts bitllets exploten la tendència dels escàners digitals a produir patrons de moaré incloent dissenys circulars o ondulats, per a que aparegui un patró de moaré quan s’escaneja o s’imprimeix.[16]
Microscòpia[modifica]
En microscòpia de super resolució, el patró de moaré es pot utilitzar per obtenir imatges amb una resolució superior al límit de difracció, mitjançant una tècnica coneguda com microscòpia d'il·luminació estructurada.[2]
En la microscòpia d'efecte túnel, apareixen franges de moaré si les capes atòmiques superficials tenen una estructura cristal·lina diferent de la del cristall a granel. Això pot ser, per exemple, a causa de la reconstrucció superficial del cristall o quan hi ha una capa fina d'un segon cristall a la superfície (per exemple, monocapa de grafè,[17][18] doble capa de grafè,[19] heteroestructura de Van der Waals de grafè i hBN (nitrur de bor hexagonal)[20][21] o nanoestructures de bismut i antimoni.[22]
En microscòpia electrònica de transmissió (TEM), les franges de moaré translacionals es poden veure com línies de contrast paral·leles formades en imatges TEM de contrast de fase per la interferència de plans de la xarxa cristal·lina difractant que se superposen i que poden tenir un espai i / o orientació diferent.[23] La majoria de les observacions de contrast de moaré descrites a la literatura s’obtenen mitjançant imatges TEM de contrast de fase d'alta resolució. Tanmateix, si s’utilitza la imatge d'un microscopi electrònic d'escombrat per transmissió corregit per aberració de gran angle de camp fosc anular (HAADF-STEM), s’obté una interpretació més directa de l'estructura cristal·lina en termes de tipus i posicions d'àtoms.[23][24]
Ciència dels materials i física de la matèria condensada[modifica]
A la física de la matèria condensada, el fenomen de moaré és habitualment en materials bidimensionals. L'efecte es produeix quan hi ha un desajustament entre el paràmetre de retícula (o l'angle de la capa 2D) i el del substrat subjacent (o una altra capa 2D),[17][18] com en les heteroestructures de materials 2D.[21][22] El fenomen s’explota com a mitjà d'enginyeria de l'estructura electrònica o propietats òptiques dels materials,[25] que alguns anomenen materials de moaré. Els canvis sovint significatius en les propietats electròniques en torçar dues capes atòmiques i la possibilitat d'aplicacions electròniques han portat al nom de twistrònica d'aquest camp. Un exemple destacat es troba en la doble capa de grafè torçat, que forma un patró de moaré i en un angle màgic particular presenta superconductivitat i altres propietats electròniques importants.[26]
-
Patró de moaré sorgit de la superposició de dues xarxes de grafè girades 4°
En ciència dels materials, els exemples coneguts que presenten contrast de moaré són, per exemple, làmines primes[27] o nanopartícules de tipus MX (M = Ti, Nb; X = C, N) superposades amb una matriu austenítica. Les dues fases, MX i la matriu, tenen una estructura cristal·lina cúbica centrada en la cara i una relació d'orientació cub sobre cub. Tanmateix, presenten un desajust significatiu de xarxa d'entre el 20 i el 24% (basat en la composició química de l'aliatge), que produeix un efecte de moaré.[24]
Referències[modifica]
- ↑ Wells, John. Longman Pronunciation Dictionary (en nglès). Pearson Longman, 2008. ISBN 978-1-4058-8118-0.
- ↑ 2,0 2,1 Gustafsson, M. G. L. «Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy». Journal of Microscopy. DOI: 10.1038/10.1046/j.1365-2818.2000.00710.x.
- ↑ «Moire in scanning» (en anglès). Scantips.
- ↑ Jain, Anil K.; Figueiredo, Mário; Zerubia, Josiane. Energy Minimization Methods in Computer Vision and Pattern Recognition (en anglès). Springer, 2001.
- ↑ Skeat, Walter. The Concise Dictionary of English Etymology (reimprés 1993) (en anglès). Wordsworth Editions, 1910, p. 289–290. ISBN 9781853263118.
- ↑ «Scanning Images in Books/Magazines/Newspapers (Moire patterns)» (en anglès). Scantips.
- ↑ Jain, Figueiredo i Zerubia, 2001.
- ↑ Miao, Houxun; Panna, Alireza; Gomella; Bennett, Eric E; et al. «A universal moiré effect and application in X-ray phase-contrast imaging» (en anglès). Nature Physics, 12(9), 2016, pàg. 830–834. Bibcode: 2016NatPh..12..830M. DOI: 10.1038/nphys3734. PMC: 5063246. PMID: 27746823.
- ↑ Hutley, M.C; Stevens «Optical Inspection of Arrays and Periodic Structures Using Moire Magnification» (en anglès). IEE Colloquium, Microengineering in Optics and Optoelectronics, 16-11-1999.
- ↑ Kamal, Hala; Völkel, Reinhard; Alda, Javier «Properties of Moiré Magnifiers» (en anglès). Optical Engineering, 37(11), novembre 1998, pàg. 3007–3014. Bibcode: 1998OptEn..37.3007K. DOI: 10.1117/1.601889.[Enllaç no actiu]
- ↑ «US Patent 4,629,325» (en anglès). Google Patents.[Enllaç no actiu]
- ↑ Trabas, Alexander. «Prohibited anchorage» (en anglès). Light of Lights.
- ↑ «Inogen light (sic)». A: Hydrographic Dictionary (en anglès). Mònaco: International Hydrographic Organization, 2003, p. 113.
- ↑ Kazda, Antonín; Caves, Robert. Airport design and operation (en anglès). Bingley, England: Emerald, 2015, p. 204–205. ISBN 9781784418700.
- ↑ «Scanning Images in Magazines/Books/Newspapers» (en anglès). ScanTips.
- ↑ Sincerbox, Glenn T. Counterfeit deterrent features for the next-generation currency design (en anglès). Washington, DC: National Materials Advisory Board, 1991, p. 61. ISBN 9780309050289.
- ↑ 17,0 17,1 Kobayashi, Katsuyoshi «Moiré pattern in scanning tunneling microscopy: Mechanism in observation of subsurface nanostructures» (en anglès). Physical Review B, 53(16), 01-01-1996, pàg. 11091–11099. Bibcode: 1996PhRvB..5311091K. DOI: 10.1103/PhysRevB.53.11091. PMID: 9982681.
- ↑ 18,0 18,1 N’Diaye, Alpha T «Two-Dimensional Ir Cluster Lattice on a Graphene Moiré on Ir(111)» (en anglès). Physical Review Letters, 97(21), 01-01-2006, pàg. 215501. arXiv: cond-mat/0609286. Bibcode: 2006PhRvL..97u5501N. DOI: 10.1103/PhysRevLett.97.215501. PMID: 17155746.
- ↑ Schouteden, K; Galvanetto, N «Scanning probe microscopy study of chemical vapor deposition grown graphene transferred to Au(111)» (en anglès). Carbon, 95, 2015, pàg. 318–322. DOI: 10.1016/j.carbon.2015.08.033.
- ↑ Tang, Shujie; Wang, Haomin; Zhang, Yu; Li, Ang; et al. «Precisely aligned graphene grown on hexagonal boron nitride by catalyst free chemical vapor deposition» (en anglès). Scientific Reports, 3(1), 16-09-2013, pàg. 2666. arXiv: 1309.0172. Bibcode: 2013NatSR...3E2666T. DOI: 10.1038/srep02666. PMC: 3773621. PMID: 24036628.
- ↑ 21,0 21,1 Tang, Shujie; Wang, Haomin; Wang, Huishan «Silane-catalysed fast growth of large single-crystalline graphene on hexagonal boron nitride» (en anglès). Nature Communications, 6, 2015, pàg. 6499. arXiv: 1503.02806. Bibcode: 2015NatCo...6.6499T. DOI: 10.1038/ncomms7499. PMC: 4382696. PMID: 25757864.
- ↑ 22,0 22,1 Le Ster, Maxime; Maerkl, Tobias; Kowalczyk, Pawel J; Brown, Simon A «Moiré patterns in van der Waals heterostructures» (en anglès). Physical Review B, 99(7), 2019, pàg. 075422. Bibcode: 2019PhRvB..99g5422L. DOI: 10.1103/PhysRevB.99.075422.
- ↑ 23,0 23,1 Williams, David B; Carter, C. Barry. Transmission electron microscopy: a textbook for materials science (en anglès), 1 de gener de 2009, p. 393–397. ISBN 9780387765013. OCLC 876600051.
- ↑ 24,0 24,1 Heczko, M; Esser, B.D; Smith, T.M; Beran, P; et al. «Atomic resolution characterization of strengthening nanoparticles in a new high-temperature-capable 43Fe-25Ni-22.5Cr austenitic stainless steel» (en anglès). Materials Science and Engineering: A, 719, 14-03-2018, pàg. 49–60. DOI: 10.1016/j.msea.2018.02.004. ISSN: 0921-5093.
- ↑ Liu, Yuan; Weiss, Nathan O; Duan, Xidong; Cheng, Hung-Chieh; et al. «Van der Waals heterostructures and devices» (en anglès). Nature Reviews Materials, 1(9), 2016, pàg. 16042. Bibcode: 2016NatRM...116042L. DOI: 10.1038/natrevmats.2016.42. ISSN: 2058-8437.
- ↑ «Trend: Bilayer Graphene's Wicked, Twisted Road» (en anglès). APS Physics.
- ↑ Yin, Xi; Liu, Xinhong; Pan, Yung-Tin; Walsh, Kathleen A; Yang, Hong «Hanoi Tower-like Multilayered Ultrathin Palladium Nanosheets» (en anglès). Nano Letters, 14(12), 10-12-2014, pàg. 7188–7194. Bibcode: 2014NanoL..14.7188Y. DOI: 10.1021/nl503879a. PMID: 25369350.
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Patró de moaré |
- Una sèrie de pintures a l'oli basades en els principis del patró de moaré de l'artista britànic Pip Dickens
- Una demostració de l'efecte de moaré causat per les interferències entre cercles
- Un exemple interactiu de diversos patrons de moaré
- Efecte de moaré de fase: patró de moaré en una pantalla darrere de dues màscares de fase transparents quan la pantalla s’allunya
- Plantilles fora del centre en operadors Laplacians
- The Moiré Effect Lights That Guide Ships Home, un video de YouTube de Tom Scott, sobre la llum Inogon a Southampton (anglès)

























![{\displaystyle {\begin{aligned}f_{1}&={\frac {1+\sin(k_{1}x)}{2}}\\[4pt]f_{2}&={\frac {1+\sin(k_{2}x)}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c7aa17b59e171f087bf00e4ea25e757a420e7e2)
![{\displaystyle {\begin{aligned}f_{3}&={\frac {f_{1}+f_{2}}{2}}\\[5pt]&={\frac {1}{2}}+{\frac {\sin(k_{1}x)+\sin(k_{2}x)}{4}}\\[5pt]&={\frac {1+\sin(Ax)\cos(Bx)}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/299a140b39d9049c8ad1ae2ee4043a02799b5fa5)













![{\displaystyle {\begin{aligned}(2D)^{2}&={\frac {p^{2}}{\sin ^{2}\alpha }}(1+\cos \alpha )^{2}+p^{2}\\[5pt]&=p^{2}\cdot \left({\frac {(1+\cos \alpha )^{2}}{\sin ^{2}\alpha }}+1\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/229b539abf32cf81b046f267e761623c1f39c6ce)
![{\displaystyle {\begin{aligned}(2D)^{2}&=2p^{2}\cdot {\frac {1+\cos \alpha }{\sin ^{2}\alpha }}\\[5pt]D&={\frac {\frac {p}{2}}{\sin {\frac {\alpha }{2}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d648b415b71837decbbb11a15395c1011654df07)
























