Teorema de Ptolemeu
En geometria euclidiana, el teorema de Ptolemeu és una relació entre els quatre costats i dues diagonals d'un quadrilàter cíclic (un quadrilàter els vèrtexs del qual es troben en un cercle comú). El teorema rep el nom de l'astrònom i matemàtic grec Ptolemeu (Κλαύδιος Πτολεμαῖος; Claudius Ptolemaeus).[1] Ptolemeu va utilitzar el teorema com a ajuda per crear la seva taula de cordes, una taula trigonomètrica que va aplicar a l'astronomia.
-
El teorema de Ptolemeu és una relació entre aquestes longituds en un quadrilàter cíclic.
Si els vèrtexs del quadrilàter cíclic són A, B, C i D en ordre, aleshores el teorema diu que:
on les línies verticals denoten la longitud dels segments de línia entre els vèrtexs anomenats. Aquesta relació es pot expressar verbalment de la següent manera:
Si un quadrilàter és inscriptible en un cercle, el producte de les longituds de les seves diagonals és igual a la suma dels productes de les longituds dels parells de costats oposats.
A més, la inversa del teorema de Ptolemeu també és certa:
En un quadrilàter, si la suma dels productes de les longituds dels seus dos parells de costats oposats és igual al producte de les longituds de les seves diagonals, aleshores el quadrilàter es pot inscriure en un cercle, és a dir, és un quadrilàter cíclic.
El text de Ptolemeu[modifica]
Text grec del Llibre I, capítol 10 de l'Almagest diu:
| « | (grec antic) Ὅν δὲ τρόπον καὶ αἱ λοιπαὶ τῶν κατὰ μέρος [ἐν τῷ κύκλῳ εὐθείων] δοθήσονται, δείξομεν ἐφεξῆς προεκθέμενοι λημμάτιον εὔχρηστον πάνυ πρὸς τὴν παροῦσαν πραγματείαν. Ἔστω γὰρ κύκλος ἐγγεγραμμένον ἔχων τετράπλευρον τυχὸν τὸ ΑΒΓΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΓ καὶ ΒΔ. Δεικτέον ὅτι τὸ ὑπὸ τῶν ΑΓ καὶ ΒΔ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ συναμφοτέροις τῷ τε ὑπὸ τῶν ΑΒ, ΔΓ καὶ τῷ ὑπὸ τῶν ΑΔ, ΒΓ.
|
(català) Com les altres [línies inscrites al cercle] també es donaran part per part, ho mostrarem immediatament proposant un petit lema molt pràctic per a la present consideració. Sigui una circumferència que conté qualsevol quadrilàter inscrit ABCD, i connectem les rectes AG i BD. Es demostrarà que el rectangle contingut per AC i BD és igual a la suma del contingut per AB, DG i el contingut per AD, BG. | » |
| — Claudi Ptolemeu, Almagest, Llibre I, cap. 10 | |||
Enunciats moderns[modifica]
El producte de les longituds de les diagonals de qualsevol quadrilàter inscriptible és igual a la suma dels productes de les longituds dels seus costats oposats.— Teorema de Ptolemeu (implicació directa)
Es pot estendre a una equivalència:
Es pot estendre a punts d'una línia i, de manera més general, s'indica de la següent manera:
Quatre punts i d'un espai euclidià són cocíclics o alineats, si i només si entre els tres productes , un és la suma dels altres dos.— Teorema de Ptolemeu (en general)
Exemples[modifica]
Triangle equilàter[modifica]
El teorema de Ptolemeu dóna com a corol·lari un bonic teorema[2] sobre un triangle equilàter inscrit en una circumferència.
Donat un triangle equilàter inscrit en una circumferència i un punt sobre la circumferència.
La distància del punt al vèrtex més llunyà del triangle és la suma de les distàncies del punt als dos vèrtexs més propers.
Demostració: és conseqüència immediata del teorema de Ptolemeu:
Quadrat[modifica]
Qualsevol quadrat pot estar inscrit en una circumferència, el centre del qual és el centre del quadrat. Si la longitud comuna dels seus quatre costats és igual a aleshores la longitud de la diagonal és igual a segons el teorema de Pitàgores i la relació òbviament es manté.
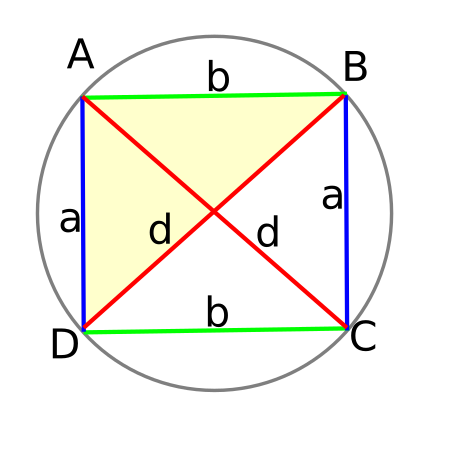
Rectangle[modifica]
De manera més general, si el quadrilàter és un rectangle amb els costats a i b i la diagonal d aleshores el teorema de Ptolemeu es redueix al teorema de Pitàgores. En aquest cas el centre de la circumferència coincideix amb el punt d'intersecció de les diagonals. El producte de les diagonals és llavors d2, el costat dret de la relació de Ptolemeu és la suma a2 + b2.
-
Teorema de Pitàgoras: «manifestum est». Copèrnic
Copèrnic, que va utilitzar àmpliament el teorema de Ptolemeu en el seu treball trigonomètric, es refereix a aquest resultat com un «porisme» o corol·lari evident:[3]
A més, està clar («manifestum est») que quan s'ha donat l'acord que subtendeix un arc, també es pot trobar aquest acord que subtendeix la resta del semicercle.
Pentàgon[modifica]
Un exemple més interessant és la relació entre la longitud a del costat i la longitud (comuna) b de les 5 cordes d'un pentàgon regular.
-
La proporció àuria es desprèn d'aquesta aplicació del teorema de Ptolemeu
En completar el quadrat, la relació dóna la proporció àuria:[Nota 1]
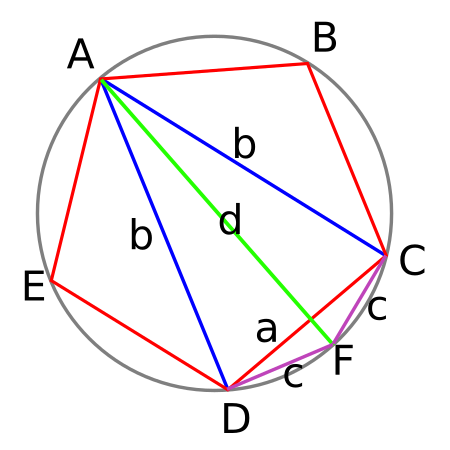
Costat del decàgon[modifica]
Si ara es dibuixa el diàmetre AF en bisectant DC de manera que DF i CF siguin els costats c d'un decàgon inscrit, es pot tornar a aplicar el teorema de Ptolemeu,
aquesta vegada al quadrilàter cíclic ADFC amb el diàmetre d com una de les seves diagonals:
- on és la proporció àuria.
- [Nota 2]
d'on s'obté el costat del decàgon inscrit en funció del diàmetre del cercle. El teorema de Pitàgores aplicat al triangle rectangle AFD dóna llavors «b» en termes de diàmetre i «a» el costat del pentàgon[Nota 3] es calcula després com:
Com va escriure Copèrnic (seguint Ptolemeu),[4]
Demostracions[modifica]
Demostració visual[modifica]
La següent animació mostra una demostració visual del teorema de Ptolemeu, basada en [Derrick i Herstein 2012, p. 386]:[5]
-
Demostració visual animada del teorema de Ptolemeu, basada en [Derrick i Herstein 2012, p. 386]
Demostració per semblança de triangles[modifica]
Sigui ABCD un quadrilàter cíclic. A la corda BC, els angles inscrits ∠BAC = ∠BDC, i en AB, ∠ADB = ∠ACB. Es construeix K sobre AC de manera que ∠ABK = ∠CBD; a partir de ∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD, ∠CBK = ∠ABD.
-
Construccions per a una demostració del teorema de Ptolemeu
Ara, pels angles comuns △ABK és semblant a △DBC, i així mateix △ABD és semblant a △KBC. Llavors AK/AB = CD/BD, i CK/BC = DA/BD; de manera equivalent, AK⋅BD = AB⋅CD, i CK⋅BD = BC⋅DA. Sumant dues igualtats tenim AK⋅BD + CK⋅BD = AB⋅CD + BC⋅DA, i factoritzant això dóna (AK+CK)·BD = AB⋅CD + BC⋅DA. Però AK+CK = AC, com AC⋅BD = AB⋅CD + BC⋅DA, Q.E.D..[6]
La demostració tal com està escrita només és vàlida per a quadrilàters cíclics simples. Si el quadrilàter s'autocreua, K estarà situat fora del segment de línia AC. Però en aquest cas, AK−CK = ±AC, donant el resultat esperat.
Demostració amb identitats trigonomètriques[modifica]
Fem que els angles inscrits delimitats per , i siguin, respectivament, , i , i el radi del cercle sigui . Llavors tenim , , , , i , i la igualtat original a demostrar es la transformem en
d'on el factor ha desaparegut dividint els dos costats de l'equació per aquest.
Ara utilitzant les fórmules de suma, i , és trivial demostrar que ambdós costats de l'equació anterior són iguals a
Aquí hi ha una altra prova, potser més transparent, utilitzant una trigonometria rudimentària.
Definim un nou quadrilàter inscrit en el mateix cercle, on són els mateixos que a , i , estirat en la mateixa corda que , és definit per , .
Llavors, té les mateixes longituds d'arestes i, per tant, els mateixos angles inscrits delimitats per les arestes corresponents, com , només en un ordre diferent. Això és, , i , per, respectivament, i . També, i tenen la mateixa àrea. Llavors,
Demostració per inversió[modifica]
Triem un cercle auxiliar de radi centrat en D respecte al qual el circumcicle d'ABCD s'inverteix en una línia (vegeu la figura següent).
-
Demostració del teorema de Ptolemeu mitjançant inversió de cercles
Aleshores Llavors i també es pot expressar com , i respectivament. Multiplicant cada terme per i utilitzant dóna la igualtat de Ptolemeu.
S'ha de tenir en compte que si el quadrilàter no és cíclic, llavors A', B' i C' formen un triangle i, per tant, A'B'+B'C' > A'C', donant-nos una demostració molt senzilla de la desigualtat de Ptolemeu[Nota 4] que es presenta a continuació.
Demostració usant nombres complexos[modifica]
Inserim ABCD en mitjançant la identificació com quatre punts diferents . Definim
- .
Llavors
amb igualtat si i només si . Això demostra la desigualtat de Ptolemeu en general, ja que només queda demostrar que es troben disposats consecutivament sobre un cercle (possiblement de radi infinit, és a dir, una línia) en si i només si .
De la forma polar d'un nombre complex , s'obté
amb l'última igualtat si i només si ABCD és cíclic, ja que un quadrilàter és cíclic si i només si els angles oposats sumen .
S'ha de tenir en compte que aquesta demostració es fa de manera equivalent observant que la ciclicitat d'ABCD, és a dir, la suplementarietat i , és equivalent a la condició
- ;
en particular hi ha una rotació de en què aquest és 0 (és a dir, els tres productes són nombres reals positius), i pel qual el teorema de Ptolemeu
llavors s'estableix directament a partir de la identitat algebraica simple
Corol·laris[modifica]
En el cas d'un cercle de diàmetre unitari, els costats de qualsevol quadrilàter cíclic ABCD són numèricament iguals als sinus dels angles i que delimiten.
De la mateixa manera, les diagonals són iguals al sinus de la suma del parell d'angles que delimiten. Aleshores podem escriure el teorema de Ptolemeu en la forma trigonomètrica següent:
Aplicant determinades condicions als angles delimitats i és possible derivar una sèrie de corol·laris importants utilitzant l'anterior com a punt de partida. En el que segueix és important tenir en compte que la suma d'angles .
Corol·lari 1. Teorema de Pitàgores[modifica]
Sigui i . Llavors
-
Corol·lari 1: Teorema de Pitàgores
(ja que els angles oposats d'un quadrilàter cíclic són suplementaris). Aleshores:[Nota 5]
Corol·lari 2. La llei del cosinus[modifica]
Sigui . El rectangle del corol·lari 1 és ara un trapezi simètric amb diagonals iguals i un parell de costats iguals. Els costats paral·lels difereixen en longitud unitats, on:
-
Corol·lari 2: Llei del cosinus
En aquest cas, serà més fàcil tornar a l'enunciat estàndard del teorema de Ptolemeu:
La regla del cosinus per al triangle ABC.
Corol·lari 3. Angle compost sinus (+)[modifica]
Sigui
Llavors
Per tant,
Fórmula per a angle compost sinus (+).[7]
Corol·lari 3. Angle compost sinus (-)[modifica]
Sigui . Llavors . Per tant,
Fórmula per a angle compost sinus (−).[7]
Aquesta derivació correspon al Tercer Teorema tal com el narra Copèrnic després de Ptolemeu a Almagest. En particular, si es donen els costats d'un pentàgon (delimitats 36° a la circumferència) i d'un hexàgon (delimitats 30° a la circumferència), es pot calcular una corda delimitada 6°. Aquest va ser un pas crític en l'antic mètode de càlcul de taules de cordes.[Nota 6]
Corol·lari 3. Angle compost cosinus (+)[modifica]
Aquest corol·lari és el nucli del Cinqué Teorema tal com el narra Copèrnic després de Ptolemeu a Almagest.
Sigui . Llavors . Per tant
Fórmula per a angle compost cosinus (+)
Tot i no tenir la destresa de la nostra notació trigonomètrica moderna, hauria de quedar clar dels corol·laris anteriors que en el teorema de Ptolemeu (o més simplement el Segon Teorema) el món antic tenia a la seva disposició una eina trigonomètrica extremadament flexible i poderosa que permetia amb el coneixement de la seva època elaborar taules de cordes precises (corresponents a taules de sinus) i utilitzar-les en els seus intents d'entendre i mapejar el cosmos tal com el veien. Com que Hiparc va elaborar taules de cordes tres segles abans de Ptolemeu, hem de suposar que coneixia el «Segon Teorema» i els seus derivats. Seguint el rastre dels antics astrònoms, la història registra el catàleg d'estrelles de Timocaris d'Alexandria. Si, com sembla probable, la compilació d'aquests catàlegs requeria una comprensió del «Segon Teorema», aleshores els veritables orígens d'aquest últim desapareixen després en la boira de l'antiguitat, però no pot ser descabellat suposar que els astrònoms, arquitectes i enginyers de construcció de l'Antic Egipte podria haver-ne tingut algun coneixement.
Desigualtat de Ptolemeu[modifica]
L'equació del teorema de Ptolemeu mai és certa amb els quadrilàters no-cíclics. La desigualtat de Ptolemeu és una extensió d'aquest fet, i és una forma més general del teorema de Ptolemeu. Afirma que, donat un quadrilàter ABCD, aleshores
on la igualtat es compleix si i només si el quadrilàter és cíclic. Aquest cas especial és equivalent al teorema de Ptolemeu.
Teorema relacionat sobre la ràtio de les diagonals[modifica]
Un quadrilàter no creuat es pot escriure si i només si les longituds dels costats i de les diagonals compleixen la relació:— Segon teorema de Ptolemeu
El teorema de Ptolemeu dóna el producte de les diagonals (d'un quadrilàter cíclic) coneixent els costats, el següent teorema dóna el mateix per a la ràtio de les diagonals.[8]
Demostració: se sap que l'àrea d'un triangle inscrita en un cercle de diàmetre és:
-
Aquest és un quadrilàter no-cíclic. La igualtat mai es manté aquí, i és desigual en la direcció indicada per la desigualtat de Ptolemeu
Si escrivim l'àrea del quadrilàter com la suma de dos triangles que comparteixen el mateix cercle circumscrit, obtenim dues relacions per a cada descomposició.
Igualant, obtenim la fórmula anunciada.
Conseqüència: Coneixent tant el producte com la relació de les diagonals, en deduïm les expressions immediates:
Ús per Ptolemeu[modifica]

Ptolemeu va utilitzar el primer teorema per elaborar taules trigonomètriques.[9][10] Per fer-ho, va considerar un cercle la circumferència del qual es divideix en 360 graus i el diàmetre del qual es divideix en 120 parts iguals.[Nota 7] Aleshores busca atribuir a diversos arcs de cercle la longitud de les cordes delimitats per aquests arcs.
Primer va tractar els casos d'arcs de 36°, 60°, 72°, 90°, 120° per als quals la corda delimitada és el costat respectivament del decàgon regular, l'hexàgon regular, el pentàgon regular, el quadrat, i el triangle equilàter, tots inscrit en el cercle.[11] Com que tots aquests polígons es poden construir amb un regle i un compàs, de fet podem determinar la longitud dels seus costats. Aleshores, utilitzant el fet que un triangle inscrit en un cercle és rectangle si un dels seus costats és igual al diàmetre, el teorema de Pitàgores li permet determinar les cordes associades als arcs que són els complements de 180° dels arcs anteriors.
Llavors, coneixent les cordes associades a dos arcs de cercle, utilitza el seu teorema per determinar la corda delimitada per les diferències o les sumes d'aquests arcs.[12] A la figura oposada, de fet, suposem que es coneixen les longituds de les cordes delimitades pels arcs AB i AC, així com el diàmetre AD del cercle. Els triangles BAD i CAD sent angles rectes en B i C, el teorema de Pitàgores permet determinar BD i CD. Per tant, tots els segments blaus (de la imatge de la dreta) tenen una longitud coneguda. El teorema de Ptolemeu ens permet deduir la longitud del segment vermell BC. Per tant, Ptolemeu pot determinar la longitud de la corda associada a l'angle 12° = 72° – 60°.
Veiem així que el teorema de Ptolemeu té, en les matemàtiques antigues, el paper que tenen per a nosaltres les fórmules de trigonometria (sinus i cosinus de la suma o diferència de dos angles).

Ptolemeu també sap determinar la corda delimitada per mig arc.[13] A la figura oposada, sigui BC l'arc del qual coneixem la corda, i AC el diàmetre del cercle. Pel teorema de Pitàgores al triangle rectangle ABC, també coneixem la longitud AB. Tracem la bisectriu (AD) de l'angle BAC, de manera que BD = CD. Continuem [AC] el punt E tal que AE = AB. Aleshores, els triangles ABD i AED són isomètrics. Per tant, tenim CD = BD = ED i el triangle ECD és isòsceles. La seva alçada (DZ) talla (AC) en Z, mig de [EC]. Però EC es coneix perquè EC = AC – AE = AC – AB, i AB i AC es coneixen. Així doncs, es coneix ZC, la meitat d'EC. Per tant es coneix la corda desitjat CD, perquè, en el triangle rectangle ACD, tenim (Euclides VI.8). Coneixent la corda de 12°, Ptolemeu pot completar la seva taula calculant les longituds de les cordes associades als arcs de 6°, 3°, 1°30' i 45'.
Per tant, no pot obtenir la longitud de la corda que subtendeix un arc d'1°. Obté aquest valor mitjançant una interpolació resultant dels valors obtinguts per als arcs d'1°30' i 45'.[14] Aleshores dedueix la corda que delimita l'arc de 30', i finalment pot elaborar una taula dels arcs i les seves cordes delimitades, mig grau per mig grau.[15]
En el sisè volum de l'Almagest, Ptolemeu dóna un valor aproximat del nombre π obtingut gràcies al valor de la corda delimitada per un angle d'un grau. De fet, multiplicant aquest valor (1° 2'50") per 360 per fer una revolució completa, s'obté 377" unitats, el diàmetre de les quals és 120". En altres paraules, troba que π val aproximadament .[16]
Notes[modifica]
- ↑ La Proposició 8 del Llibre xiii d'Elements d'Euclides demostra amb triangles similars el mateix resultat: és a dir, que la longitud a (el costat del pentàgon) divideix la longitud b (unint vèrtexs alternatius del pentàgon) en «proporció mitjana i extrema».
- ↑ I de manera anàloga, la Proposició 9 del Llibre xiii d'Elements d'Euclides demostra amb triangles semblants que la longitud c (el costat del decàgon) divideix el radi en «proporció mitjana i extrema».
- ↑ A la referència següent es pot trobar un article interessant sobre la construcció d'un pentàgon regular i la determinació de la longitud dels costats: [1]
- ↑ La desigualtat de Ptolemeu afirma que la part de l'esquerra de la igualtat anterior és sempre major o igual a la de la dreta. Els únics casos d'igualtat que admet són quan el quadrilàter és cíclic. Això també es pot interpretar a conseqüència de la fórmula de Bretschneider (vegeu Fórmula de Brahmagupta).
- ↑ A De Revolutionibus Orbium Coelestium (DROC), Copèrnic no es refereix al teorema de Pitàgores pel seu nom, sinó que utilitza el terme «porisme», una paraula que en aquest context particular semblaria denotar una observació o una conseqüència òbvia d'un altre teorema existent. El «porisme» es pot veure a les pàgines 36 i 37 del DROC (Harvard electronic copy).
- ↑ Per entendre el Tercer Teorema, compareu el diagrama de Copèrnic que es mostra a la pàgina 39 del De Revolutionibus Orbium Coelestium amb la derivació de sin(A-B) que es troba a la pàgina web Cut the knot.
- ↑ La raó és que Ptolemeu realitza els seus càlculs en el sistema sexagesimal tant per a angles com per a longituds, i un radi de 60 parts s'adapta bé a aquest sistema.
Referències[modifica]
- ↑ Ptolemeu, 148, p. Llibre 1, cap. 10.
- ↑ Wilson, Jim. «Ptolemy's Theorem» (en anglès).
- ↑ Copèrnic, 1543, p. 37. Vegeu les dues últimes línies d'aquesta pàgina. Copèrnic es refereix al teorema de Ptolemeu com "Theorema Secundum"..
- ↑ Copèrnic, 1543, p. Liber Primus: Theorema Primum.
- ↑ Derrick i Herstein, 2012, p. 386.
- ↑ Alsina i Nelsen, 2010, p. 112.
- ↑ 7,0 7,1 «Sine, Cosine, and Ptolemy's Theorem» (en anglès). Cut the knot.
- ↑ Alsina i Nelsen, 2010, p. 112-113.
- ↑ Colette, 1973, p. 93-94.
- ↑ Morris, 1972, p. 122-126.
- ↑ Ptolemeu, 148, p. Vol 1, p. 28.
- ↑ Ptolemeu, 148, p. Vol. 1, p. 30.
- ↑ Ptolemeu, 148, p. Vol 1. p. 31.
- ↑ Ptolemeu, 148, p. Vol. 1, p. 34-36.
- ↑ Ptolemeu, 148, p. Vol. 1, p. 38.
- ↑ Berggren, Borwein i Borwein, 1999, p. 678.
Bibliografia[modifica]
- Alsina, Claudi; Nelsen, Roger B. Charming Proofs: A Journey Into Elegant Mathematics (en anglès). 42. Mathematical Association of America, 2010 (Dolciani Mathematical Expositions). ISBN 9780883853481.
- Amarasinghe, G. W. I. S «A Concise Elementary Proof for the Ptolemy's Theorem» (
 PDF) (en anglès). Global Journal of Advanced Research on Classical and Modern Geometries (GJARCMG), 2(1), 2013, pàg. 20-25.
PDF) (en anglès). Global Journal of Advanced Research on Classical and Modern Geometries (GJARCMG), 2(1), 2013, pàg. 20-25. - Berggren, Lennard; Borwein, Jonathan; Borwein, Peter. Pi: A Source Book (en anglès). Springer, 1999. ISBN 978-0-387-98946-4.
- Colette, Jean-Paul. Histoire des mathématiques (en francès). 1. Vuibert, 1973. ISBN 978-2-711-71020-3.
- Kline, Morris. Mathematical Thought from Ancient to Modern Times (en anglès). Oxford University Press, 1972.
- Copèrnic, N. De Revolutionibus Orbium Coelestium (en llatí), 1543.
- Derrick, W.; Herstein, J. «Proof Without Words: Ptolemy's Theorem» (en anglès). The College Mathematics Journal, 43(5), 2012.
- Coxeter, H. S. M; Greitzer, S. L «Ptolemy's Theorem and its Extensions» (en anglès). Geometry Revisited. Mathematical Association of America, 2.6, 1967, pàg. 42-43.
- Ptolemeu, Claudi. Almagest (en grec antic), 148.
Vegeu també[modifica]
Enllaços externs[modifica]
|
|
Els enllaços externs d'aquest article necessiten una revisió: la Viquipèdia no és un directori d'internet. |
- «Proof of Ptolemy's Theorem for Cyclic Quadrilateral» (en anglès). Mathalino.
- «On Ptolemy's Theorem» (en anglès). MathPages.
- Elert, Glenn. «Ptolemy's Table of Chords» (en anglès). E-World, 1994.
- «Ptolemy's Theorem» (en anglès). Cut-the-knot.
- «Ptolemy Inequality» (en anglès). MathWorld.
- Warendorff, Jay. «Ptolemy's Theorem» (en anglès). The Wolfram Demonstrations Project.
- «Book XIII» (en anglès). Euclid's Elements.



















![Demostració visual animada del teorema de Ptolemeu, basada en [Derrick i Herstein 2012, p. 386]](http://upload.wikimedia.org/wikipedia/commons/3/30/Animated_visual_proof_of_Ptolemy%27s_theorem%2C_based_on_Derrick_%26_Herstein_%282012%29.gif)













































![{\displaystyle {\begin{aligned}\arg(\zeta )&=\arg {\frac {(z_{A}-z_{B})(z_{C}-z_{D})}{(z_{A}-z_{D})(z_{B}-z_{C})}}\\&=\arg(z_{A}-z_{B})+\arg(z_{C}-z_{D})-\arg(z_{A}-z_{D})-\arg(z_{B}-z_{C}){\pmod {2\pi }}\\&=\arg(z_{A}-z_{B})+\arg(z_{C}-z_{D})-\arg(z_{A}-z_{D})-\arg(z_{C}-z_{B})-\arg(-1){\pmod {2\pi }}\\&=-\left[\arg(z_{C}-z_{B})-\arg(z_{A}-z_{B})\right]-\left[\arg(z_{A}-z_{D})-\arg(z_{C}-z_{D})\right]-\arg(-1){\pmod {2\pi }}\\&=-\angle ABC-\angle CDA-\pi {\pmod {2\pi }}\\&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7495b8234bfa9430c32f8c1f040a91ac7eba361f)



![{\displaystyle \arg \left[(z_{A}-z_{B})(z_{C}-z_{D})\right]=\arg \left[(z_{A}-z_{D})(z_{B}-z_{C})\right]=\arg \left[(z_{A}-z_{C})(z_{B}-z_{D})\right]{\pmod {2\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbf0944740e62d3f9e28eb2b11fcb20a4282fa3)



















![{\displaystyle {\begin{array}{lcl}S_{1}S_{3}+S_{2}S_{4}={\overline {AC}}\cdot {\overline {BD}}\\\Rightarrow S_{1}S_{3}+{S_{2}}^{2}={\overline {AC}}^{2}\\\Rightarrow S_{1}[S_{1}-2S_{2}\cos(\theta _{2}+\theta _{3})]+{S_{2}}^{2}={\overline {AC}}^{2}\\\Rightarrow {S_{1}}^{2}+{S_{2}}^{2}-2S_{1}S_{2}\cos(\theta _{2}+\theta _{3})={\overline {AC}}^{2}\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d3b16a07f677bb51d957d63b99d753abd6cb68f)


















![{\displaystyle {\begin{aligned}AC^{2}&=AC\cdot BD\cdot {\frac {AC}{BD}}=(AB\cdot CD+BC\cdot DA){\frac {AB\cdot DA+BC\cdot CD}{AB\cdot BC+DA\cdot CD}}\\[8pt]BD^{2}&={\frac {AC\cdot BD}{\frac {AC}{BD}}}=(AB\cdot CD+BC\cdot DA){\frac {AB\cdot BC+DA\cdot CD}{AB\cdot DA+BC\cdot CD}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f73c7793ada3a03a1f4d05cfb2b29a95ce3cc568)

