Marea

Diferència entre marea baixa i marea alta al port de l'illa Ré, al golf de Biscaia

Mecanisme de les marees

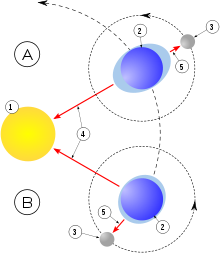
La marea és el moviment cíclic de nivell del mar i els oceans, acompanyat per un moviment ascendent (flux) i descendent (reflux). Està produït principalment per les forces de marea gravitatòries combinades que exerceixen el Sol i la Lluna. Quan aquest nivell és màxim s'anomena marea alta o plenamar, i quan aquest nivell és mínim s'anomena marea baixa o baixamar.

Segons la localització de la Terra, el cicle de flux i reflux pot ocórrer una vegada (marea diürna) o dues vegades al dia (marea semidiürna) o ser de tipus mixt. Durant la lluna plena i la lluna nova, és a dir, quan la Terra, la Lluna i el Sol són substancialment en el mateix eix (anomenat sizígia), operen junts i les marees són de major rang (marees vives). En contrast, durant el quart creixent i el quart minvant, quan els tres astres estan en quadratura la marea és inferior (marees mortes).

Les marees més baixes de l'any es produeixen normalment en els solsticis d'hivern i estiu, les més altes als equinoccis de la primavera i la tardor a causa de la declinació (5º aprox.) de l'òrbita de la Lluna respecte a l'eclíptica o òrbita aparent del Sol.

Aquest moviment de les marees no es limita a l'aigua, sinó que afecta l'escorça de la totalitat de la Terra (dites «marees de l'escorça terrestre»), encara que en menor mesura. Per tant, el que veiem a la costa és en realitat la diferència entre la marea de l'escorça i la marea de l'oceà. De manera més general, els objectes celestes estan subjectes a forces de marea prop d'altres cossos (el satèl·lit Io del planeta Júpiter està sotmès a marees colossals).

Dues marees altes successives estan separades per un període de dotze hores i mitja, de manera que entre una plenamar i una baixamar passen sis hores i quart.

En els mars tancats o petits (com el Mediterrani) les marees són gairebé imperceptibles, però en els oceans i mars oberts, en canvi, hi pot haver diferències d'alguns metres entre la baixamar i la plenamar.

La influència gravitatòria solar pot augmentar o disminuir la intensitat de les marees. Pot originar marees vives si el Sol i la Lluna estan alineats (succeeix dues vegades al mes, en lluna nova i en lluna plena), i marees mortes (quan la Lluna està en quart creixent i en quart minvant). La pressió atmosfèrica també influeix, fins a 15 cm: aquestes marees es denominen marees meteorològiques.

Etimologia

La paraula catalana marea prové del francès marée i aquest és un derivat antic del llatí mare (mar). En català està registrada des del segle xv, per exemple la fa servir el poeta Ausiàs Marc, però no és una paraula del llenguatge popular possiblement pel fet que a la Mediterrània les marees són de molt poca importància i la superen el fenomen de la rissaga el qual sí que té un nom popular.

Història

El fenomen de marees és conegut de l'antiguitat ençà. Sembla que Píteas (segle IV aC) va ser el primer a assenyalar la relació entre l'amplitud de la marea i les fases de la Lluna així com la seva periodicitat. Plini el Vell (23-79) en el seu Naturalis Història descriu correctament el fenomen i pensa que la marea està relacionada amb la Lluna i el Sol. Molt més tard, Bacon, Kepler i altres van tractar d'explicar aquest fenomen, admetent l'atracció de la Lluna i del Sol. Però va ser Isaac Newton en la seva obra Philosophiae Naturalis Principia Mathematica ('Principis matemàtics de la Filosofia Natural', 1687) qui va donar l'explicació de les marees acceptada actualment. Més tard, Pierre-Simon Laplace (1749-1827) i altres científics van ampliar l'estudi de les marees des d'un punt de vista dinàmic. Isaac Newton va realitzar diversos estudis científics del comportament de les marees i va calcular l'altura d'aquestes segons la data del mes, l'estació de l'any i la latitud. Més tard, Simon Laplace va complementar els estudis de Newton.

Coeficient de marea

A les taules de marees apareixen uns coeficients de marees que indiquen l'amplitud de la marea prevista (la diferència d'altura entre les consecutives plenamars i baixamars d'un lloc). El coeficient de marees màxim possible és 118, corresponent a la major plenamar o baixamar que pugui donar-se excloent els efectes meteorològics. Els coeficients de marees es calculen a partir dels següents paràmetres del sol i de la lluna: ascensió recta, declinació, paral·laxi i distància de la Terra a l'astre.

Tot i que els coeficients de marea són els mateixos per a tot el planeta Terra, afecten de manera molt diferent l'amplitud de les marees en funció del lloc on ens trobem. Aquesta variació d'amplitud és gairebé nul·la en els mars tancats, exceptat quan es produeixen ressonàncies locals (per exemple, arriba a ser d'1 m a Venècia); és feble enmig dels oceans, però sol amplificar-se considerablement en propagar-se fins a les costes continentals.

L'amplitud de les marees varia en l'espai i el temps:

• En l'espai, hi marees d'intensitat feble (en les àrees pròximes a l'equador terrestre, les marees a penes acostumen a arribar a una desena de centímetres). En altres llocs hi ha marees d'intensitat forta (per exemple, les costes franceses de la badia de Saint-Malo), on se superen regularment els 10 m.
• En el temps, el coeficient, i en conseqüència l'amplitud de les marees, segueixen les fases de la lluna amb lleugers desnivells en els quarts minvant i el creixent; i grans desnivells en el moment de lluna nova i lluna plena. Les diferències d'amplitud entre marees baixes i altes presenten grans contrasts. A Saint-Malo la diferència de nivell entre la plenamar i la baixamar es redueix a tres metres en períodes de marees baixes; i arriba tretze metres en període de marees altes.

Origen del fenomen

El fenomen de la marea és degut a la deformació de la superfície dels oceans com a resultat de les atraccions combinades de l'aigua sobre la Terra i els cossos celestes veïns, i a causa de l'efecte de la força centrífuga deguda la rotació de la Terra. S'expressa de forma diferent en diferents parts del món, a causa dels molts efectes addicionals: inèrcia del desplaçament d'aigua induïda per la mateixa marea i els efectes de deformació de la terra propagació de l'ona induïda diferent per factors com ara la força de Coriolis, la mida i la forma de les conques (obertes o tancades, profundes o no), etc.

Fenòmens físics

Teoria de la marea: l'atracció gravitatòria és proporcional al producte de les masses dels dos cossos que es tracti i inversament proporcional al quadrat de la distància entre ells, l'astre (principalment la Lluna en el cas de Terra) atreu masses parents (líquids i sòlids). En particular, el punt més proper de la Lluna és més atret que el seu punt oposat. Al mateix temps, l'aigua en els mars és atreta per la Terra. Un primer component de la força de marea resulta de la diferència d'atracció entre la Terra i la Lluna, segons el baricentre Terra / Lluna.

Es presenta el mateix fenomen per a tots els astres i en particular per al Sol, que encara que és lluny de la Terra, té un impacte real per la seva alta massa.

D'altra banda, la Terra gira sobre el seu eix, sotmetent els objectes de la seva superfície a una força centrífuga. D'una manera simplificada, la marea, per tant, és el resultat de la combinació d'aquestes dues forces:

• Força residual que resulta de la combinació de diferents forces d'atracció,
• Força centrífuga a causa de la rotació de la Terra.

És la combinació d'aquests dos factors el que explica la presència de dues "perles d'aigua" en ambdós costats de la Terra al llarg de l'eix de la Terra i la Lluna

D'això es desprèn una deformació de la superfície del mar, però també del sòl, que difereix del que seria sense la presència del nostre satèl·lit i del Sol

En la mar, es pot comparar aquesta deformació amb una enorme ona la qual seria una forma regular, si els fons dels oceans fossin regulars i no hi hagués costa.

Potencial generador

La presència de la Lluna i el Sol, està en l'origen de les forces de gravetat que generen les marees.

La força generadora de la marea deriva d'un potencial gravitatori relacionat amb la distància entre la Terra i la Lluna, al voltant de 380.000 km, i el radi de la Terra que és aproximadament 6.400 km. La Terra pot ser representada per un punt material ubicat al centre del nostre món i afectat per tota la massa terrestre. No obstant això, l'atracció que pateix una partícula en un punt del món difereix en amplitud.

Representació del sistema Terra/Lluna per descriure el potencial generador

$\Pi$, és el potencial d'on deriva la força generadora de la marea. En un punt de referència geocèntric s'escriu aquest potencial aplicat a un punt P de la superfície de la Terra, afectat per les coordenades $(a,\lambda ,\phi )$ sota la forma :

$\Pi _{P_{(a,\lambda ,\phi )}}=-GM_{Lune}{\Big (}{\frac {1}{d}}{\Big )}$ (eq : 1.1)

amb :

• $G$, la constant de gravitació
• $M_{Lune}$, la massa de l'astre pertorbador
• $d$, la distància entre el punt $P_{(a,\lambda ,\phi )}$ i el centre de l'astre pertorbador
• $R_{Lune}$, la distància entre el centre de la Terra i l'astre pertorbador
• $a$, el radi de la Terra
• $\psi$, l'angle zenital de l'astre pertorbador al punt $P_{(a,\lambda ,\phi )}$

Es pot expressar $d$ en funció de $a$, $R_{Lune}$ i $\psi$ per la relació sorgida del teorema d'Al Kashi :

$d^{2}=a^{2}+R_{Lune}^{2}-2a{R_{Lune}}\cos \psi$ (eq : 1.2)

si s'expressa com 1/d, l'equació anterior (eq 1.2) esdevé :

${\frac {1}{d}}={\frac {1}{R_{Lune}{\sqrt {1-2{\frac {a}{R_{Lune}}}\cos \psi +{\frac {a^{2}}{R_{Lune}^{2}}}}}}}$ (eq : 1.3)

La Lluna i el Sol són els dos únics astres en els quals la influència és notable en la generació de marees sobre la Terra, l'un per la seva proximitat i l'altre per la seva gran massa.

El terme $a/R_{Lune}$ val aproximadament $1/60$ per la Lluna i $1/2,5.10^{4}$ per al Sol. Es pot estimar que :

${\frac {a}{R_{Lune}}}<<1$

Esdevé possible descomponent (eq 1.3) sota la forma d'una sèrie en $a/R_{Lune}$ amb l'ajuda dels polinomis de Legendre.

${\frac {1}{d}}={\frac {1}{R_{Lune}}}\sum _{n=0}^{\infty }{{\Big (}P_{n}(\cos \psi ){\big (}{\frac {a}{R_{Lune}}}{\big )}^{n}{\Big )}}$

amb els polinomis de Legendre definits per :

• $P_{0}^{}(\cos \psi )=1$
• $P_{1}^{}(\cos \psi )=\cos \psi$
• $P_{2}^{}(\cos \psi )={\frac {3}{2}}\cos ^{2}\psi -{\frac {1}{2}}$
• $P_{n+1}(\cos \psi )={\frac {2n+1}{n+1}}\cos \psi .P_{n}(\cos \psi )-{\frac {n}{n+1}}.P_{n-1}(\cos \psi )$

Si es limita a l'ordre 2 que representa ja el 98% del senyal, es pot escriure el potencial (eq 1.1) sota la forma :

$\Pi _{P_{(a,\lambda ,\phi )}}=-GM_{Lune}{\Big (}{\frac {1}{d}}{\Big )}\simeq -{\frac {3}{2}}GM_{Lune}{\frac {a^{2}}{R_{Lune}^{3}}}{\Big (}\cos ^{2}\psi -{\frac {1}{3}}{\Big )}$ (eq : 1.4)

Amb les coordenades $(R_{Lune},\lambda _{Lune},\phi _{Lune})$ de l'astre i les coordenades $(R_{P},\lambda _{P},\phi _{P})$ al punt del globus terrestre P, es pot expressar $\cos(\psi )$ sota la forma :

$\cos \psi =\sin \phi _{Lune}\sin \phi _{P}^{}+\cos \phi _{Lune}\cos \phi _{P}\cos(\lambda _{P}-\lambda _{Lune})$

L'equació (eq 1.4) aleshores esdevé :

$\Pi _{P_{(a,\lambda ,\phi )}}=-{\frac {3}{4}}GM_{Lune}{\frac {a^{2}}{R_{Lune}^{3}}}{\Big [}{\frac {1}{3}}(1-3\sin ^{2}\phi _{Lune})(1-3\sin ^{2}\phi _{P})$ $+\sin(2\phi _{Lune})\sin(2\phi _{P}^{})\cos(\lambda _{P}-\lambda _{Lune})$ $+\cos ^{2}\phi _{Lune}\cos ^{2}\phi _{P}\cos 2(\lambda _{P}-\lambda _{Lune}){\Big ]}$ (eq : 1.5)

Si es detallen cadascun dels tres termes de l'equació (eq 1.5), i només es considera el moviment de rotació de la Terra un dia, es pot obtenir els termes de generació de les primeres ones de la marea.

En efecte :

1. El terme $\cos ^{2}\phi _{Lune}\cos ^{2}\phi _{P}^{}\cos 2(\lambda _{P}-\lambda _{Lune})$ efectua dos períodes en la rotació en l'angle $(\lambda _{P}-\lambda _{Lune})$ de $2\pi$ (rotació de la Terra en un dia), es descriu una funció semidiürna.
2. El terme $\sin(2\phi _{Lune})\sin(2\phi _{P})\cos(\lambda _{P}-\lambda _{Lune}^{})$ només efectua un període es descriu com fórmula diürna.
3. El terme $(1-3\sin ^{2}\phi _{Lune})(1-3\sin ^{2}\phi _{P}^{})$ no depèn pas de la longitud i només de la latitud de l'astre i del punt de mesurament, aquest terme varia en funció del moviment de declinació de l'astre (període $>>$ 24h), i descriu una funció de període llarg.

George Darwin va fer l'any 1883 càlculs i va extreure 59 termes solars i 32 termes lunars. Posteriorment Doodson va deduir 400 termes que es fan servir per donar nom a les ones.

Marees al Mediterrani

Grans marees

Localitat	Amplitud (m)
Granville, badia de la Muntanya Saint-Michel (França)	13,6
Burntcoat Head, Mines Basin, badia de Fundy (Nova Escòcia, Canadà)	11,7
Leaf Lake, badia d'Ungava (Quebec, Canadà)	9,8
Newport, canal de Bristol (Anglaterra)	9,2
Sunrise, Turnagain Arm, al Cook Inlet (Alaska, EE.Plantilla:EsdUU.)	9,2
Riu Gallegos (Reducció Beacon) (Argentina)	8,8
Entrada del riu Koksoak, a la badia de Hudson (Canadà)	8,7
Banc Direcció, a l'estret de Magallanes (Xile)	8,5

L'alçada de la marea en els ports del Mediterrani només és d'uns 10 cm, molt baixa comparada amb els 13 metres d'alguns ports de l'Atlàntic (Saint Malo o Mont Saint-Michel, per exemple). El motiu que explica la baixa incidència de les marees al Mediterrani és pel fet de ser un mar relativament petit i que cal una gran quantitat d'aigua perquè hi hagi variació del nivell de l'aigua a les costes, També influeix el relleu geogràfic del litoral donat que en les costes planes la marea avança per molt més terreny (i molt més de pressa) que en les costes irregulars.

Vegeu també

• Marea viva
• Energia mareomotriu

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Marea

• Taula de marees de diversos ports d'Espanya

Viccionari