Roda

Una roda és un dispositiu en forma disc o torus. La seva operació fonamental és transmetre el moviment lineal en moviment angular. És una de les primeres i més simples màquines. El nombre de rodes sovint classifica el vehicle que les usa en una categoria o una altra.
L'aparició de la roda, cap al 3500 aC,[1] és considerada crucial per al desenvolupament de la civilització. Permeté als humans fer un ús més eficaç de la potència animal i resoldre la seva necessitat de desplaçar-se, així com el seu ús en altres aplicacions com les rodes de terrissaire o les dels molins. Tanmateix no totes les civilitzacions van incorporar inicialment aquest invent, per desconeixement o per voluntat pròpia.
Etimologia[modifica]

La paraula roda prové del vocable llatí rota, que procedeix del protoindoeuropeu rotā-, una forma de l'arrel ret- que significa "per rodar, girar".[2] Els estudiosos han suggerit que la paraula roda té la seva arrel en les llengües dels pobles orientals més antics i que posteriorment passà al grec i al llatí amb la migració dels indoeuropeus des d'Àsia a Europa.
El terme anglès wheel provendria de varkana o mankana, que al seu torn estarien compostes de les veus var o man (amb el significat ‘treballar, operar’) i kara o kana (tronc recte, curt i de secció arrodonida).
Història[modifica]

La roda és considerada com un dels invents claus de la història de la humanitat, juntament amb el foc. Va ser inventada de manera independent per diverses cultures. És impossible saber a partir de quina idea va sorgir el primer desenvolupament de la roda, encara que és plausible teoritzar que va sorgir de l'observació directa i mimetisme de la natura. Per exemple en veure com una pedra plana es desplaça de mode dificultós amb comparació amb una pedra més proporcionada en les seves tres dimensions costera avall, o per exemple en les boles de neu, i fins i tot en els troncs de llenya.
Sumeris[modifica]

Molts autors situen la primera aparició vers el 4000 aC en les antigues cultures de Mesopotàmia durant el període sumeri. Aquí, entre el Tigris i Eufrates, han nascut les primeres civilitzacions agrícoles, ramaderes i comercials. Han nascut les ciutats i aquestes han comportat també el desenvolupament de l'ús dels metalls i de la construcció d'habitatges. A més a més, la nova organització social, on els camps de conreu i les ciutats es troben distanciats, ha fet necessària l'existència de mitjans de transports eficients.
És difícil saber com els sumeris van arribar a descobrir la roda. Tanmateix, es coneix que els terrissaires de Sumer, al sud de Mesopotàmia, coneixien el moviment circular: “Els intercanvis comercials amb altres comunitats eren cada vegada més importants per al creixement de les ciutats; calia produir més i millors peces de ceràmica. Aquesta necessitat hauria conduït al descobriment de la tècnica del torn, que efectivament va proporcionar més rapidesa i precisió en l'elaboració dels productes, a més d'una millora de la qualitat decorativa. Hom creu que el torn de terrissaire va ser l'inici d'una veritable revolució tecnològica que va culminar amb el descobriment de la roda primitiva”.[3]

La primera roda emprada en un carro de què es té constància data aproximadament del 3500 aC,[1] i va ser trobada a la ciutat d'Ur. El seu disseny és molt simple: les rodes, de forma cilíndrica, eren discs sòlids de fusta massissa i estaven formades per dos o més segments units per grapes de fusta. Les rodes s'inserien en un eix i quedaven fixades per estaques que travessaven els extrems de l'eix. Tanmateix, els historiadors argumenten que la seva invenció ha de ser anterior, probablement plataformes de fusta sota de les quals hi havia troncs cilíndrics per a facilitar el desplaçament, units i enganxats a les banyes dels bous que les arrossegaven.[3]
En qualsevol cas, la revolució dels carros va arribar un mil·lenni després de la roda d'Ur, amb la roda radiada, que apareix en la Cultura Sintashta, corresponent a la Cultura d'Andrónovo, i a Anatòlia i Síria[4] i cap al 2500 aC, els carros es transformaren en plataformes mòbils des de les quals es podien llançar javelines contra l'enemic, i permetien desplaçar els exèrcits de manera més ràpida i unitària. És a dir, van esdevenir armes de guerra.[3]
Antic Egipte[modifica]
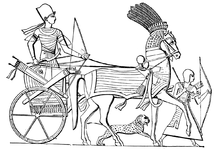
El carro com a arma de combat van fer que a l'antic Egipte implantés cap a l'any 1500 aC la innovadora roda de sis o vuit radis protegits per una llanta de fusta, amb l'objectiu d'alleugerir i fer més manejables els carros.[3]
Altres civilitzacions[modifica]
Altres aparicions independents se situen en la Xina, pel 2800 aC; i en les cultures asteca i inca en el 1500 dC, encara que aquestes últimes, per falta d'animals de càrrega, mai es va usar més que com una joguina.
Aparentment la roda ha estat desconeguda per altres cultures, com l'Àfrica subsahariana, la Polinèsia, i la ja esmentada Amèrica del Nord i del Sud. Les civilitzacions d'aquestes terres aconseguiren sobreviure i prosperar sense l'ajuda de la roda. Fins a l'edat moderna aquestes terres no van descobrir les aplicacions de la roda per al transport.
Fins i tot al Pròxim Orient, entre els segles iii i XII dC, les civilitzacions d'aquesta regió i del nord d'Àfrica van abandonar el transport amb vehicles rodats. El seu lloc el van ocupar camells perquè havien valorat que aquests animals eren més ràpids i eficients a l'hora de transportar objectes i persones: un camell pot recórrer més quilòmetres en un temps breu i consumir menys aigua i aliment que els bous que arrossegaven els carretons.[3]
Altres fonts afirmen que va néixer a Eslovènia, on el 2003 es va trobar una roda que té entre 5100 i 5350 anys.[5]
La roda moderna[modifica]

A l'Edat Medieval i el Renaixement es produïren perfeccionaments tècnics aplicats a l'enginyeria hidràulica i militar. Amb la Revolució Industrial la roda ocupa un lloc destacat perquè s'empra per a la transmissió motriu. Però, fins a la segona meitat del segle xix no es va produir la gran innovació que revolucionà el transport terrestre: l'aparició dels pneumàtics amb càmera d'aire. Cap al 1840, el britànic Charles Goodyear, després d'anys d'investigació, aconseguí obtenir la goma vulcanitzada. Cinc anys després, la va emprar Robert W. Thompson, que, unint l'elasticitat de la goma amb l'aire, feu néixer les llantes. Inicialment només van ser emprades per a bicicletes i tricicles, però aviats esdevingueren imprescindibles per a l'automòbil.[3]
La roda va ser patentada en 2001 per l'advocat australià John Keogh, amb el nom de "dispositiu d'ajuda pel transport circular". L'objectiu d'aquesta patent no era altre que demostrar les imprecisions i ineficàcies del sistema de patents modern.
Mecànica[modifica]
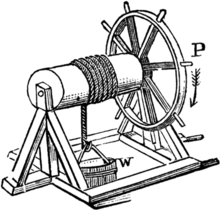
Les relacions cinemàtiques i dinàmiques bàsiques que s'estableixen entre els diferents punts de la roda s'obtenen a partir de l'estudi de la mateixa com a sòlid rígid, particularitzant-les segons la geometria particular, les condicions inicials, l'entorn, etc. Es considera roda com a màquina simple quan és suportada per un eix, fix o giratori, que passa pel seu centre. Solen muntar-se com a suport d'un mòbil, com el cos d'un vehicle, cosa que li permet avançar linealment de manera molt eficient. Si l'eix és solidari a la roda, els dos cossos giren a la mateixa velocitat com si fossin el mateix sòlid.
La roda amb eix és una de les sis màquines simples. Aquestes tenen la propietat d'aconseguir un avantatge mecànic, que fa que e que multiplica el parell torsor en aplicar una força.
El funcionament de les rodes es basa en l'adherència de la superfície d'aquestes al terreny, la qual cosa permet al vehicle disposar d'un sistema de suport al terreny que minimitza les pèrdues d'energia a les ineficiències pròpies degudes a l'elasticitat de la roda i a les pèrdues de rendiment originades als suports mitjançant coixinets de rodolament. Quan les rodes es fan servir per a moure vehicles per damunt de superfícies és important també la superfície a la qual s'adhereixen, que pot ser un camí o carretera o sobre les vies del ferrocarril gràcies a l'encanalament de la roda.
Geometria de les rodes[modifica]
Les rodes es basen en la geometria del cercle. Dels cercles es tenen els paràmetres:
- Diàmetre: És interessant notar que a les rodes sol determinar-se la mida pel diàmetre, ja que es tracta de la màxima distància entre dos punts d'una roda i, per tant, la màxima restricció en termes d'espai.
- Perímetre: És la distància recorreguda per una roda en un pla al girar una revolució. D'aquesta manera, la distància recorreguda per a un nombre determinat de revolucions depèn del perímetre que al mateix temps depèn del diàmetre segons la següent expressió:
Que ve d'una expressió més general:
On:
- és la distància recorreguda
- és l'angle girat
- r és el radi de la roda (D=2r)
Moviment circular[modifica]
Vegeu l'article principal Moviment circular

El problema de moviment rectilini uniforme és equivalent al del rotacional. Les variables rectilínies distància, velocitat i acceleració són equivalents a les variables angulars: angle, velocitat angular i acceleració angular respectivament. Totes tres, segons s'ha vist a l'apartat de geometria es troben relacionades cinemàticament amb les variables lineals:[6]
- Angle:
- Velocitat angular:
- Acceleració angular:
On, generalitzant per les tres, es té:
- A l'esquerra de la igualtat la magnitud angular (angle, velocitat angular o acceleració angular)
- A la dreta de la igualtat es troba la magnitud lineal equivalent (distància, velocitat lineal, acceleració lineal) multiplicada pel radi r
Les tres relacions anteriors són degudes a la geometria de la roda, de la que es desprèn que l'arc de circumferència corresponent a un determinat angle girat és el producte de l'angle expressat en radians pel radi de la circumferència. Això és el cas particular del que s'ha vist abans, ja que al recórrer una revolució d'una roda de radi r, es recorre el perímetre P = 2π r, que correspon a un angle girat de 2π rad per volta.
Finalment, l'acceleració centrípeta per tal de calcular el lligam expressat forma d'acceleració d'un punt situat a la roda que gire amb ella, situat a un determinat radi r és:
On:
- ac és una acceleració dirigida sempre cap al centre de la roda
- és la velocitat angular de la roda
- r és el radi on se situa el punt estudiat

L'acompliment del rodolament de les rodes depèn de la perfecta adherència amb la superfície sobre la qual rodola. A qualsevol mòbil dotat de rodes, hi ha una fricció entre el pneumàtic i la carretera en el punt de contacte de la roda amb aquesta, de manera que el moviment relatiu en aquest punt de la roda respecte de la carretera és nul. La cinemàtica de les rodes pot explicar-se com es mostra a la figura, tractant-se d'un problema de mecànica de medis continus si es coneix la velocitat d'un punt d'aquest es desprèn un camp de velocitats la velocitat de qualsevol punt VP és:[7]
On:
- és la velocitat del punt amb velocitat coneguda.
- és el vector velocitat angular de la roda respecte al terreny.
- és el vector de posició relativa entre els dos punts.
Com es coneix que l'adherència ha de ser efectiva, és evident que la velocitat al punt de contacte relativa al terreny ha de ser 0, en el cas contrari la roda aniria lliscant. De l'anterior equació es desprèn una relació lineal entre la magnitud de les velocitats de qualsevol punt relatives a terra i la distància d'aquestos al punt de contacte al pla de rotació.
Gràcies al coneixement de la cinemàtica del moviment dels sòlids en rotació, podria fer-se la descomposició de velocitats en dos parts:
- La velocitat lineal deguda a la rotació als punts de la roda
- La velocitat lineal del centre de la roda
D'aquesta manera es descompon la velocitat en dos: Per una banda la velocitat que percebria un observador muntat a la roda i per l'altra la del vehicle en moviment. És evident que als punts situats al radi més exterior la velocitat de rotació és igual a la lineal. Això s'explica intuïtivament, ja que per fer una revolució completa, el vehicle ha de recórrer una distància igual al perímetre de la roda.[6]
Avantatge mecànic i forces a la superfície[modifica]

Com les altres cinc màquines simples, la roda amb eix té un efecte multiplicador sobre les forces, és a dir, un avantatge mecànic. L'avantatge mecànic de les rodes com a màquina simple depèn del diàmetre de la roda i de l'eix de transmissió. Al generar un parell de forces a l'eix (de menor diàmetre que la roda) es transmet un moment torsor a la roda. La roda, que normalment es troba damunt una superfície o sotmesa a una càrrega resistent, transmet forces a través de les forces de contacte de la seua superfície amb altres cossos.
L'expressió que lliga forces i parell és la del moment de forces:
En el cas invers, amb l'aplicació de forces a la superfície de la roda, es genera un moment que provoca un parell. De la mateixa manera que a les palanques, aquest parell depèn de la força i del radi al qual s'aplica, de manera que amb la mateixa força F es pot aconseguir un major parell si es té una roda de major radi r.
L'avantatge mecànic ideal, suposant condicions sense altres interaccions que les càrregues de treball a l'eix i a la roda, es calcula amb la següent fórmula:
On:
- i és l'avantatge mecànic ideal.
- RR és el radi de la roda.
- RE és el radi de l'eix.
Mentre que si es prenen mesures reals, es podria definir com a:
On:
- Ar és l'avantatge mecànic real.
- R és la força resistent de la càrrega a l'eix.
- Er és la força real que s'aplica a la roda.
A les aplicacions de la roda als vehicles motoritzats es poden donar els dos casos, tant la transmissió de parell del motor a les rodes, com la transmissió de forces al vehicle degut a la mateixa velocitat de desplaçament.
El primer cas es dona a l'eix de tracció o de propulsió del vehicle, quan es transmet un moment resultant del parell motor transmès a l'eix de la roda. En aquest cas ja s'ha vist que a la superfície de contacte de la roda amb el sòl es transmet una força F, en sentit contrari al d'avanç del vehicle. La clau de la tracció amb rodes és disposar d'adherència en tot moment, cosa que provocarà una força de reacció deguda a la fricció estàtica del contacte de la roda amb el sòl. Aquesta força d'adherència D és una força de reacció i per tant és de sentit contrari a la de tracció de la roda.
Així doncs, la força motriu a les rodes de tracció/propulsió dels vehicles és la mateixa reacció a la tracció de la roda, causant de l'adherència del vehicle, que a més és externa al vehicle per ser causada pel sòl.
Aquesta força d'adherència depèn directament de la càrrega de la roda i de les condicions del camí. En el cas que la força de tracció estigui per damunt de la màxima fricció estàtica, aleshores la roda lliscarà, a causa del fet que la resultant de forces de contacte deixaria de ser nul·la.[8]
Inèrcia de rotació i efecte giroscòpic[modifica]
La inèrcia de les rodes dels vehicles durant el seu moviment és una qüestió important, degut a la contribució que aporten a la dinàmica total del vehicle. Per ser un cas especial de sòlid en moviment combinat de rotació i de translació, s'estudia l'energia cinètica de les rodes gràcies a la contribució deguda a la velocitat dels dos moviments per separat, amb una velocitat v de translació i una velocitat ω de rotació. L'energia cinètica de la roda és doncs:[9]
On:
- E és l'energia cinètica de la roda deguda a la contribució de rotació i de translació.
- m és la massa de la roda.
- I és el moment d'inèrcia polar.
- v és la velocitat de translació.
- ω és la velocitat de rotació.

Girant a altes velocitats angulars, és notable una altra característica essencial de la roda. Es tracta de l'efecte giroscòpic que estabilitza la roda al girar sobre el seu eix, cosa que és d'ajuda per a mantenir l'estabilitat del vehicle, que és d'especial ajuda als vehicles de dues rodes.[10]
Aquest efecte es deu al moment angular de les rodes al girar amb una velocitat fixa sobre el seu eix, en el cas de moviment d'un vehicle. En condicions inercials de moviment uniforme i rectilini del vehicle el moment angular no canvia.
En el cas dels vehicles de dues rodes, l'estabilitat i la maniobrabilitat des del punt de vista del conductor és deguda a la capacitat que té de variar el moment angular gràcies a la inclinació del vehicle respecte del pla vertical. Per exemple, un conductor que incline el vehicle cap a l'esquerra convertirà el moviment de les rodes en un moviment de precessió, cosa que farà girar el vehicle cap a l'esquerra.[10] Aquestes forces solen ser més significatives als vehicles amb majors velocitats i rodes més grans (amb majors moments d'inèrcia, com per exemple les motocicletes, mentre que resulten ser minses a les bicicletes on s'empren rodes lleugeres i amb menys velocitats.
En el cas de rodes girant i desplaçant-se lliurement, és coneguda la capacitat de les rodes de mantenir-se rodolant pel pla horitzontal fins que perden la velocitat. El moment angular de les rodes en rotació oposa resistència als seus canvis i converteix el moviment en estable quan se sotmet a la roda a petites pertorbacions.
Pèrdues per rodament[modifica]


El rendiment de la transmissió de forces al terreny a les rodes en moviment és el principal factor per escollir la roda com a mitjà de transport. Tot i això, als estudis detallats sobre rendiment de rodes es consideren quatre contribucions que causen pèrdues d'eficiència durant el moviment:
- El treball de flexió del cos de la roda al passar per la zona de contacte.
- El treball de la roda al comprimir o penetrar el terreny.
- El treball de fricció originat a possibles lliscaments
- El treball de fricció de la roda amb l'aire:
- Interior: En el cas de rodes amb càmera d'aire.
- Exterior: Per la interacció de la superfície de la roda i dels radis d'aquesta amb l'aire que l'envolta.
D'aquestes ineficiències només se solen considerar les dues primeres, i se sol extreure un coeficient de resistència al rodament considerant-les de manera combinada. Normalment el coeficient depèn del terreny sobre el que circula el vehicle, una mesura de la rigidesa de les rodes i del seu diàmetre.[11] El coeficient de resistència al rodament f és emprat d'igual manera que el de fricció, amb el que s'obté la força resistent al moviment Rr multiplicant-lo pel pes del cos W·f.
Per entendre la física del funcionament no ideal, s'hauria d'aïllar el sistema de la roda i de representar el terreny i el pes de càrrega mitjançant forces puntuals. S'ha de considerar també que ni les rodes ni el terreny són rígids, cosa que modifica el diagrama de forces. En el cas real, les pèrdues són degudes a la deformació tant de la roda com del terreny. Degut a aquestes deformacions instantànies tant a roda com al terreny sorgeixen ineficiències, ja que no tot el treball de deformació a la roda o al terreny torna a convertir-se en energia mecànica.[12] Certa part d'aquesta energia és transferida al terreny i certa part retorna en forma de calor a través de la superfície de la roda o causa un augment de l'energia tèrmica a l'interior d'aquesta.
A la Figura es pot veure el cas al qual la roda és completament rígida. Es tracta de la representació d'una roda que gira de dreta cap a esquerra, amb una sèrie de forces. Cal notar que es representa una superfície de rodolament deformada, de manera que es pugui apreciar la contribució de la força de reacció N. En aquest cas particular la N no només compensa la força del pes, també és la reacció a la força de penetració de la roda sobre el terreny, amb component horitzontal no nul·la, que s'oposa al moviment. En resum, les forces a considerar són:
- F, la força exercida en el sentit del moviment, que es pot representar en forma de força horitzontal de l'eix o bé d'un parell torsor també transmès per aquest.
- W, el pes amb el que es carrega la roda.
- N, la normal que s'oposa al moviment, notar que degut a les deformacions possibles tant en el terreny com en la roda, aquesta força es troba lleugerament desviada respecte de la vertical.
L'altre cas particular a considerar és el de l'elasticitat de la roda circulant sobre terreny rígid. El cas de la resistència al rodolament degut a la deformació de la roda, en moviment estacionari la deformació es deu a la càrrega vertical amb el pes sobre la roda, de manera que es tendeix a aplanar la roda en la zona de contacte. Al girar, arriba un punt en què la superfície de la roda es comença a comprimir, fins que al passar el punt de contacte el procés de compressió s'inverteix i es comença a descomprimir[13]
Durabilitat dels pneumàtics[modifica]
En l'actualitat es fa ús intensiu a les rodes als mitjans de transport. Encara i les elevades exigències i el desgast a què estan sotmeses, es desenvolupen rodes amb pneumàtics amb capacitat de duració de 40.000 a 80.000 km.[14]
Al cas particular dels avions les rodes són sotmeses a càrregues molt fortes i a frenades molt energètiques, la qual cosa fa que el desgast sigui molt elevat, no només en la superfície de la roda, també en els suports.
Rodes per a vehicles[modifica]

Zonalment es pot dividir la roda en tres parts:
- Llanda: És la part exterior de la roda, dissenyada per tal d'afegir el pneumàtic. En el cas de les bicicletes la llanda té forma de cercle acanalat que s'uneix per tot el seu interior a l'eix gràcies als radis. La introducció de les llandes de ferro fou gràcies a la millora de les rodes de fusta al primer mil·lenni abans de Crist.[15]
- Disc: És l'estructura en forma de disc que serveix per a unir la llanda amb la part interior de la roda. La fixació interior amb el cub s'efectua mitjançant femelles fàcilment desmuntables.[9]
- Cub: És l'element que permet la unió d'aquesta amb l'eix. Es considera com a part essencial del sistema eix-roda, encara que no es pot considerar estrictament com a part de la roda i no figura dins d'aquesta en algunes publicacions.[15][9]
Rodes d'automòbils[modifica]
Els automòbils moderns s'equipen amb rodes fàcilment desmuntables, facilitant així el canvi de rodes del vehicle.
Segons el tipus de disc, es poden distingir tres tipus de rodes per automòbils:[15]
- De disc d'acer temperat: Que solen tenir forma cònica.
- De disc d'aliació lleugera: D'alt rendiment per les característiques millorades de relació resistència/pes i millor transmissió de calor.
- De radis: Unides al cub gràcies als fils d'arams en tensió que les fan més lleugeres, encara que més costoses i difícils de mantenir.
Materials[modifica]
Mentre que les primeres rodes es van fer de fusta, més tard, a l'Edat de Bronze ja s'arribaren a fer llantes de metall gràcies als avenços en la metal·lurgia. Amb la invenció de la màquina de vapor i el motor de combustió externa, comencen a sorgir majors exigències a les rodes dels vehicles, que ja es feien d'acer. Més tard es proveeix a aquesta roda d'acer d'un tub de material rodant. L'ús de rodes amb radis permeté també equipar vehicles lleugers com les bicicletes o algunes motocicletes.
Alternatives a la roda[modifica]
Les rodes no van bé per a tots els terrenys. Aquesta és la principal causa per l'elecció d'un altre sistema més adequat per circular pel terreny desitjat. Una llista d'alternatives per aquest i d'altres motius diferents pot ser:
- Lliscant per la superfície, amb el cas particular dels trineus, que poden ser una bona alternativa en terres plenes de neu o gel, ja que llisquen per la seva superfície. Es poden arrossegar mitjançant animals, a mà o si és un pendent, deixant-se caure pel pes.
- Elevació per sobre del terreny per mitjans electromagnètics (Tren Maglev) com a transport col·lectiu.
- Elevació per sobre del terreny gràcies a la pressió de l'aire (aerolliscador) com a transport amfibi.
- Muntar un animal de sella.
- Fent servir la força humana:
- Caminant amb les pròpies cames.
- Portant algú al damunt o amb una cadira.
- Fent servir una màquina de caminar
Símbols de la roda[modifica]
En el Budisme, la roda és una metàfora conceptual central. Segons aquesta religió, la vida és un cicle de naixements i reencarnacions, del qual sols es pot escapar assolint la il·luminació (o Bodhi). D'aquesta manera, la roda té podria ser l'equivalent a una creu per a un cristià o una lluna creixent per a un musulmà, encara que no és el símbol de la deïtat. La mandala és una representació comuna d'aquest concepte, i està basada en la imatge d'una roda.
En les antigues religions solars, la roda convivia amb el carro per simbolitzar el cicle del sol, que surt i es pon com fent una roda al voltant de la terra.
La roda apareix a la bandera índia per simbolitzar la llei. En canvi a la bandera gitana fa referència al passat nòmada, sempre en moviment, d'aquest poble.
És un símbol del canvi a força cultures, d'aquí deriven imatges com la roda de la fortuna
Bibliografia[modifica]
- Joaquim Agulló i Batlle, Mecànica de la partícula i del sòlid rígid, Publicacions OK Punt, 1995, ISBN 84-920850-0-2
Vegeu també[modifica]
Referències[modifica]
- ↑ 1,0 1,1 Bunch, Bryan H.; Hellemans, Alexander. The history of science and technology: a browser's guide to the great discoveries, inventions, and the people who made them, from the dawn of time to today (en anglès). Houghton Mifflin Harcourt, 2004, p.31. ISBN 0618221239.
- ↑ «ret- The American Heritage® Dictionary of the English Language: Fourth Edition. 2000». Arxivat de l'original el 2009-01-25. [Consulta: 5 juliol 2009].
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 Aguilera, Gemma. “Una història rodada”. A revista Sàpiens, número 15. Gener de 2004.
- ↑ (en anglès) Elena Efimovna Kuzʹmina i J. P. Mallory, The origin of the Indo-Iranians, V.3, p.256
- ↑ March 27, 2003 ejemplar de Ameriška Domovina [American Home]
- ↑ 6,0 6,1 «Center of gravity and Rotational variables» (en anglès), 2000. [Consulta: 8 juliol 2009].
- ↑ Falqués Serra, Albert; Marquès, Francesc; Sánchez, Joan. «Mecànica racional, Tema 6: Cinemàtica del sòlid rígid». ETSE de Camins Canals i Ports, UPC. Arxivat de l'original el 2009-12-13. [Consulta: 8 juliol 2009].
- ↑ Alonso, José Manuel. Paraninfo. Sistemas de transmisión y frenado, 1996. ISBN 84-283-2291-0.
- ↑ 9,0 9,1 9,2 Boisseaux, M. Paraninfo. Automóvil, cálculo de piezas, 1969.
- ↑ Taborek, Jaroslav J. «Resisting forces» (en anglès). [Consulta: 8 juliol 2009].
- ↑ «Understanding Horsepower». Nitrod Performance Meters. [Consulta: 17 juliol 2009].
- ↑ Heisler, Heinz. Edward Arnold. Advanced vehicle technology (en anglès), 1989.
- ↑ Watts, Lyle F. «Conserve your country's rubber» (en anglès), 1942.
- ↑ 15,0 15,1 15,2 Arias-Paz, Manuel. Dossat 2000. Manual de Automóviles (en castellà). 55a ed., 2004.