Teoria de Galois

En matemàtiques, la teoria de Galois és un conjunt de resultats que connecten la teoria de cossos amb la teoria de grups.^[1] La teoria de Galois té aplicació en diversos problemes de la teoria de cossos, i gràcies a aquesta teoria, es poden reduir a problemes més senzills de la teoria de grups. La teoria de Galois pren el nom del matemàtic francès Évariste Galois (1811-1832), mort a l'edat de 20 anys.^[1]

Aplicacions de la teoria de Galois[modifica]

El naixement de la teoria de Galois estigué motivada per l'intent de respondre a la següent qüestió:

Per què no existeix una fórmula per a la resolució d'equacions polinòmiques de cinquè grau (o superior) en termes dels coeficients del polinomi, usant operacions algebraiques (suma, resta, multiplicació, divisió) i l'extracció d'arrels (arrels quadrades, cúbiques, etc.); tal com existeix per a les equacions de segon, tercer i quart grau

El teorema d'Abel-Ruffini que és part de la teoria de Galois dona una resposta a aquesta pregunta. La teoria de Galois proporciona no només una elegant resposta a aquesta qüestió, sinó que també explica en detall per què és possible resoldre equacions de grau inferior al quart, i per quina les solucions són expressables mitjançant operacions algebraiques i extracció d'arrels.

A més la teoria de Galois proporciona respostes a problemes clàssics de la constructibilitat mitjançant la construcció amb regle i compàs. De fet, la teoria de Galois estableix quan és possible construir una certa longitud proporcional a una donada, i gràcies a això poden respondre's a les següents preguntes:

Quins polígons regulars són construïbles mitjançant regle i compàs?^[2]

Per què no és possible la trisecció de l'angle?

Història[modifica]

Història prèvia[modifica]

La teoria de Galois té els seus orígens en l'estudi de funcions simètriques – els coeficients d'un polinomi mònic són (llevat de signe) el polinomi simètric elemental en les arrels. Per exemple, $(x - a)(x - b) = x 2 - (a + b) x + ab$ , on 1, $a + b$ i $ab$ són els polinomis elementals de grau 0, 1 i 2 en dues variables.

El matemàtic francès François Viète, en les seves fórmules, va ser el primer a formalitzar això al segle XVI, pel cas d'arrels reals positives. En l'opinió del matemàtic britànic del segle XVIII Charles Hutton,^[3] l'expressió de coeficients d'un polinomi en termes de les arrels (no només per a arrels positives) va ser entesa per primer cop pel matemàtic francès del segle XVII Albert Girard; Hutton va escriure:

...[Girard va ser] la primera persona que va entendre la doctrina general de la formació dels coeficients de les potències de la suma de les arrels i dels seus productes. Va ser el primer a descobrir les regles de sumar les potències de les arrels de qualsevol equació.

En aquesta línia, el discriminant és una funció simètrica en les arrels que reflexa propietats de les arrels - és zero si i només si el polinomi té una arrel múltiple, i per a polinomis quadràtics i cúbics és positiu si i només si totes les arrels són reals i diferents, i negativa si i només si hi ha una parella d'arrels complexes conjugades.

El cas cúbic va ser resolt parcialment per primer cop pel matemàtic italià Scipione del Ferro, que tanmateix no va publicar els seus resultats. Tot i això, el seu mètode només resolia un tipus d'equació cúbica. Aquesta solució va ser posteriorment redescoberta de manera independent l'any 1535 per Niccolo Tartaglia, que la va compartir amb Girolamo Cardano, demanant-li que no la publiqués. Llavors, Cardano va estendre el seu resultat a nombrosos altres casos, utilitzant arguments similars. Després del descobriment de l'obra de del Ferro, li va semblar que el mètode de Tartaglia ja no era secret, i per tant va publicar la seva solució en el seu Ars Magna de 1545.^[4] El seu estudiant Lodovico Ferrari va resoldre el polinomi quàrtic; la seva solució també es va incloure a l'Ars Magna. En aquest llibre, tanmateix, Cardano no va proporcionar cap "fórmula general" per a la resolució de l'equació cúbica, ja que ni tenia els nombres complexes a la seva disposició, ni tenia la notació algebraica que li permetés descriure una equació cúbica general. Mitjançant notació moderna i els nombres complexos, les fórmules d'aquest llibre funcionen en el cas general, però Cardano no ho sabia això. Va ser Rafael Bombelli el primer a entendre com treballar amb nombres complexos per tal de resoldre tot tipus d'equacions cúbiques.

L'article de Réflexions sur la résolution algébrique des équations (1770) del matemàtic franco-italià Joseph Louis Lagrange va fer un pas més, introduint el mètode dels resolvents de Lagrange i analitzant la solució de les equacions cúbiques i quàrtiques de Cardano i Ferrari considerant-les en termes de permutacions de les seves arrels, que donava lloc a un polinomi auxiliar de grau inferior, conferint una entesa de les solucions i posant les bases per la teoria de grups i la teoria de Galois. Tanmateix, de forma crucial, no va considerar la composició de permutacions. El mètode de Lagrange no s'estenia a equacions quíntiques o superiors, ja que els resolvents tenien grau superior.

Paolo Ruffini gairebé va demostrar que el cas de cinquè grau no té solucions per radicals l'any 1799. La seva observació clau va ser utilitzar els grups de permutacions, no només una única permutació. La seva solució tenia una mancança, que Cauchy va considerar menor, tot i que no es va acabar de resoldre fins al treball del matemàtic noruec Niels Henrik Abel, que va publicar una demostració l'any 1824, establint doncs el teorema d'Abel-Ruffini.

Mentre que Ruffini i Abel van establir que el l'equació general de cinquè grau no es podia resoldre, algunes equacions quíntiques en particular es poden resoldre, com ara $x 5 - 1 = 0$ , i el criteri precís sobre si es pot determinar si una equació donada de grau cinc o superior es pot resoldre o no va ser descobert per Évariste Galois, que va demostrar que si un polinomi és resoluble o no és equivalent a si el grup de permutacions de les seves arrels -en termes moderns, el seu grup de Galois - té una certa estructura – en termes moderns, sobre si és o no és un grup resoluble. Aquest grup era sempre resoluble per polinomis de grau quatre o inferior, però no ho era sempre en polinomis de grau cinc i superior, cosa que explica que no hi hagi una solució general per graus alts.

Textos de Galois[modifica]

L'any 1830 Galois (als 18 anys) va enviar a l'Acadèmia Francesa de les Ciències una memòria sobre la seva teoria de resolubilitat per radicals; l'article de Galois va ser rebutjat en última instància l'any 1831 en ser massa vague i en donar una condició en termes de les arrels de l'equació en comptes dels seus coeficients. Poc després, el 1832, Galois va morir en un duel, i el seu article, "Mémoire sur les conditions de résolubilité des équations par radicaux", no veuria la llum fins al 1846 quan va ser publicat per Joseph Liouville juntament amb algunes explicacions seves.^[5] Abans de la seva publicació, Liouville va enunciar el resultat de Galois a l'Acadèmiia en un discuurs que va donar el 4 de juliol de 1843.^[6] Segons el matemàtic Allan Clark, la caracterització de Galois "supera dramàticament l'obra d'Abel i Ruffini."^[7]

Conseqüències[modifica]

La teoria de Galois era notòriament difícil d'entendre pels seus contemporanis, especialment fins al nivell de poder estendre-la. Per exemple, en el seu text de 1846, Liouville es va perdre completament en l'essència de teoria de grups del mètode de Galois.^[8] Joseph Alfred Serret que va assistir a algunes de les xerrades de Liouville, va incloure la teoria de Galois (en la tercera edició) del seu llibre de text de 1866 Cours d'algèbre supérieure. Un alumne de Serret, Camille Jordan, va entendre la teoria fins i tot millor, tal com es va reflectir en el seu llibre de 1870 Traité des substitutions et des équations algébriques. Fora de França, la teoria de Galois es va mantenir en la foscor durant més temps. A Gran Bretanya, Cayley no va aconseguir entendre-la profundament i els llibres de text britànics d'àlgebra més populars ni tan sols van mencionar la teoria de Galois fins ven entrat el segle. Al Alemanya, els escrits de Kronecker es van centrar més en el resultat d'Abel. Dedekind no va escriure gaire sobre la teoria de Galois, però en va parlar en una classe a Göttingen l'any 1858, mostrant-ne una molt bona comprensió.^[9] Els llibre d'Eugen Netto dels anys 1880, basats en el Traité de Jordan, van fer la teoria de Galois més accessible a un públic alemany i americà més ampli així com també ho va fer el llibre de text d'àlgebra de Heinrich Martin Weber.^[10]

Enfocament[modifica]

Si tenim un polinomi pot succeir que algunes de les seves arrels tinguin lligams entre elles mitjançant diverses equacions algebraiques, és a dir que compleixin aquestes equacions. Per exemple, pot succeir que per a dues de les arrels, diguem A i B, l'equació A² + 5B³ = 7 sigui certa. La idea central de la teoria de Galois és el considerar aquelles permutacions de les arrels que tinguin la propietat que qualsevol equació algebraica satisfeta per elles sigui satisfeta també després de la permutació o l'arranjament. És important assenyalar que ens restringim a equacions algebraiques els coeficients de les quals són nombres racionals. Es poden especificar certs cossos per als coeficients, però en els exemples s'utilitzen els nombres racionals. El conjunt de tals permutacions formaran un grup de permutacions, també anomenat Grup de Galois del polinomi (sobre els nombres racionals). Un exemple:

Primer exemple — equació quadràtica[modifica]

Sigui l'equació quadràtica

x² − 4x + 1 = 0.

Mitjançant l'ús de la fórmula per l'equació quadràtica sabem que les seves dues arrels són

A = 2 + √3, i

B = 2 − √3.

Algunes de les equacions algebraiques que satisfan A i B són

A + B = 4, i

AB = 1.

En cadascuna d'aquestes equacions és clar que si intercanviem els papers de A i B obtenim equacions vàlides. Però, encara que no sigui tan obvi, això és cert per a qualsevol equació algebraica que satisfan A i B. Per a provar-ho es requereix la teoria dels polinomis simètrics.

Concloem que el grup de Galois del polinomi x² − 4x + 1 consisteix en dues permutacions: la identitat que deixa A i B quietes, i la transposició, que intercanvia A i B. Com grup, és isomorf al grup cíclic d'ordre dos, denotat Z/2Z.

Podríem plantejar l'objecció que existeix aquesta altra equació satisfeta per A i B: :A − B − 2√3 = 0, però que no és certa quan intercanviem els papers. No obstant això hem d'observar que no ens importa, ja que els seus coeficients no són racionals; √3 és irracional.

De forma semblant podem parlar de qualsevol polinomi quadràtic ax² + bx + c, on a, b i c són nombres racionals.

Si el polinomi té només una arrel, per exemple x² − 4x + 4 = (x−2)², llavors el grup de Galois és trivial; això és, conté només a la permutació identitat.
Si té dues arrels racionals diferents, per exemple x² − 3x + 2 = (x−2)(x−1), el grup és de nou trivial.
Si té dues arrels irracionals (inclusivament el cas en el qual ambdues són nombres complexos), llavors el grup de Galois conté dues permutacions, com en l'exemple anterior.

Segon exemple: quelcom més enginyós[modifica]

Considere's el següent polinomi:

x⁴ − 10x² + 1,

que pot escriure's també com:

(x² − 5)² − 24.

Desitgem descriure el grup de Galois d'este polinomi, novament sobre el cos dels nombres racionals. El polinomi té quatre arrels:

A={\sqrt {2}}+{\sqrt {3}}

B={\sqrt {2}}-{\sqrt {3}}

C=-{\sqrt {2}}+{\sqrt {3}}

D=-{\sqrt {2}}-{\sqrt {3}}

Existeixen 4! = 24 maneres de permutar aquestes quatre arrels, però no totes aquestes permutacions són membres del grup de Galois. Els membres del grup de Galois han de preservar qualsevol equació algebraica amb coeficients racionals A, B, C i D. Una de dites equacions és per exemple:

A + D = 0

Ja que posat que

A+C=2{\sqrt {3}}\neq 0

,

la permutació

(A, B, C, D) → (A, B, D, C)

no està permesa, perquè transforma l'equació vàlida A + D = 0 en l'equació invàlida A + C = 0).

Una altra equació que les arrels satisfan és:

(A + B)² = 8.

Açò exclouria més permutacions, com per exemple:

(A, B, C, D) → (A, C, B, D).

Continuant d'aquesta manera, podem trobar que només les permutacions que satisfan les dues equacions anteriors simultàniament són:

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

i per tant el grup de Galois és isomorf al grup de Klein.

Grups solubles i solució per radicals[modifica]

Es diu que una arrel α es pot expressar en radicals si α és element d'un cos K tal que $F=K_{0}\subset K_{1}\subset \cdots \subset K_{s}=K$ on $K_{i+1}=K_{i}({\sqrt[{n_{i}}]{a_{i}}})\,\exists \,a_{i}\in K_{i},i=0,1,\ldots ,s-i$ Una equació polinomial és soluble per radicals si totes les arrels es poden expressar en radicals.^[11] Amb la teoria de Galois, és possible derivar el teorema següent:

El polinomi f(x) (en el cos F) és resoluble per radicals sí i només sí el seu grup de Galois és resoluble.^[12]

Un exemple quíntic no resoluble[modifica]

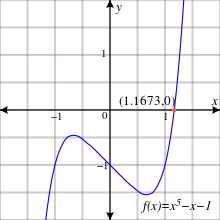
Van der Waerden^[13] va citar el polinomi $f (x) = x 5 - x - 1$ . A partir del teorema de l'arrel racional, aques polinomi no té zeros racionals. Tampoc no té factors lineals mòdul 2 o 3.

El grup de Galois de $f (x)$ mòdul 2 és cíclic d'ordre 6, ja que $f (x)$ mòdul 2 factoritza en polinomis d'ordres 2 i 3, $(x 2 + x + 1)(x 3 + x 2 + 1)$ .

$f (x)$ mòdul 3 no té factors lineals o quadràtics, i per tant és irreductible. Per tant el seu grup de Galois mòdul 3 conté un element d'ordre 5.

Se sap^[14] que un grup de Galois mòdul un nombre primer és isomòrfic a un subgrup de Galois sobre els racionals. Un grup de permutacions de 5 objectes amb elements d'ordres 6 i 5 ha de ser el grup simètric $S 5$ , que és per tant un grup de Galois de $f (x)$ . Aquest és un dels exemples més simples d'un polinomi quíntic no resoluble. Segons Serge Lang, a Emil Artin li encantava aquest exemple.^[15]

El problema invers de Galois[modifica]

El problema invers de Galois planteja si tot grup finit pot ser el grup de Galois d'alguna extensió dels números racionals. Aquest problema, proposat inicialment al segle XIX per Hilbert, roman sense resoldre.^[16]

Sempre i quan no s'especifiqui també el cos base, el problema no és gaire difícil, i tots els grups finits apareixen com a grups de Galois. Per mostrar això, es pot procedir com segueix. Trii's un cos $K$ i un grup finit $G$ . El teorema de Cayley estableix que $G$ és (llevat d'un isomorfisme) un subgrup d'un grup simètric $S$ en els elements de $G$ . Triin-se ${x α}$ no determinats, un per cada element $α$ de $G$ , i uneixin-se en $K$ per obtenir el cos $F = K ({x α})$ . Contingut en $F$ es troba el cos $L$ de funcions racionals simètriques en ${x α}$ . El grup de Galois de $F / L$ és $S$ , mitjançant un resultat bàsic atribuït a Emil Artin. $G$ actua en $F$ per restricció de l'acció de $S$ . Si el cos fix d'aquesta acció és $M$ , llavors, en virtut del teorema fonamental de la teoria de Galois, el grup de Galois de $F / M$ és $G$ .

Referències[modifica]

↑ ^1,0 ^1,1 «Évariste Galois». Gran Enciclopèdia Catalana. [Consulta: 29 octubre 2022].
↑ Stewart, Ian. Galois Theory. Chapman and Hall, 1989. ISBN 0-412-34550-1.
↑ Funkhouser 1930
↑ Cardano 1545
↑ Tignol, Jean-Pierre. Galois' Theory of Algebraic Equations. World Scientific, 2001, p. 232–3, 302. ISBN 978-981-02-4541-2.
↑ Stewart, 3rd ed., p. xxiii
↑ Clark, Allan. Elements of Abstract Algebra. Courier, 1984, p. 131. ISBN 978-0-486-14035-3.
↑ Wussing, Hans. The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory. Courier, 2007, p. 118. ISBN 978-0-486-45868-7.
↑ Scharlau, Winfried; Dedekind, Ilse; Dedekind, Richard. Richard Dedekind 1831–1981; eine Würdigung zu seinem 150. Geburtstag. Braunschweig: Vieweg, 1981. ISBN 9783528084981.
↑ Galois, Évariste; Neumann, Peter M. The Mathematical Writings of Évariste Galois. European Mathematical Society, 2011, p. 10. ISBN 978-3-03719-104-0.
↑ Dummit, David S.; Foote, Richard M. Abstract Algebra (en anglès). 3^a. Hoboken: Wiley, 2004, p. 627. ISBN 978-0-471-43334-7.
↑ Dummit, David S.; Foote, Richard M. Abstract Algebra (en anglès). 3^a. Hoboken: Wiley, 2004, p. 628-29. ISBN 978-0-471-43334-7.
↑ van der Waerden, Modern Algebra (1949 English edn.), Vol. 1, Section 61, p.191
↑ Prasolov, V.V.. «5 Galois Theory Theorem 5.4.5(a)». A: Polynomials. 11. Springer, 2004, p. 181–218. DOI 10.1007/978-3-642-03980-5_5. ISBN 978-3-642-03979-9.
↑ Lang, Serge. Algebraic Number Theory. 110. Springer, 1994, p. 121. ISBN 9780387942254.
↑ Vila, Núria «On the inverse problem of Galois theory» (en anglès). Publicacions Matemàtiques, 36, 2B, 1992, pàg. 1053-1073. Arxivat de l'original el 4 d'abril de 2010 [Consulta: 6 abril 2009]. Arxivat 2010-04-04 a Wayback Machine.

Bibliografia[modifica]

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Teoria de Galois

Baker, A. (2004): Una introducció a la Teoria Galois Arxivat 2017-09-21 a Wayback Machine., Universitat de Glasgow. (anglès)

[gec_evariste_galois-1] 1,0 ^1,1 «Évariste Galois». Gran Enciclopèdia Catalana. [Consulta: 29 octubre 2022].

[Stewart-2] Stewart, Ian. Galois Theory. Chapman and Hall, 1989. ISBN 0-412-34550-1.

[3] Funkhouser 1930

[4] Cardano 1545

[Tignol2001-5] Tignol, Jean-Pierre. Galois' Theory of Algebraic Equations. World Scientific, 2001, p. 232–3, 302. ISBN 978-981-02-4541-2.

[6] Stewart, 3rd ed., p. xxiii

[Clark1984-7] Clark, Allan. Elements of Abstract Algebra. Courier, 1984, p. 131. ISBN 978-0-486-14035-3.

[Wussing2007-8] Wussing, Hans. The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory. Courier, 2007, p. 118. ISBN 978-0-486-45868-7.

[Scharlau1981-9] Scharlau, Winfried; Dedekind, Ilse; Dedekind, Richard. Richard Dedekind 1831–1981; eine Würdigung zu seinem 150. Geburtstag. Braunschweig: Vieweg, 1981. ISBN 9783528084981.

[GaloisNeumann2011-10] Galois, Évariste; Neumann, Peter M. The Mathematical Writings of Évariste Galois. European Mathematical Society, 2011, p. 10. ISBN 978-3-03719-104-0.

[11] Dummit, David S.; Foote, Richard M. Abstract Algebra (en anglès). 3^a. Hoboken: Wiley, 2004, p. 627. ISBN 978-0-471-43334-7.

[12] Dummit, David S.; Foote, Richard M. Abstract Algebra (en anglès). 3^a. Hoboken: Wiley, 2004, p. 628-29. ISBN 978-0-471-43334-7.

[13] van der Waerden, Modern Algebra (1949 English edn.), Vol. 1, Section 61, p.191

[14] Prasolov, V.V.. «5 Galois Theory Theorem 5.4.5(a)». A: Polynomials. 11. Springer, 2004, p. 181–218. DOI 10.1007/978-3-642-03980-5_5. ISBN 978-3-642-03979-9.

[15] Lang, Serge. Algebraic Number Theory. 110. Springer, 1994, p. 121. ISBN 9780387942254.

[16] Vila, Núria «On the inverse problem of Galois theory» (en anglès). Publicacions Matemàtiques, 36, 2B, 1992, pàg. 1053-1073. Arxivat de l'original el 4 d'abril de 2010 [Consulta: 6 abril 2009]. Arxivat 2010-04-04 a Wayback Machine.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]