Vés al contingut

Paritat del zero: diferència entre les revisions

De la Viquipèdia, l'enciclopèdia lliure
Edició següent →
Contingut suprimit Contingut afegit
VisualWikitext
Pàgina nova, amb el contingut: «El nombre zero (0) és parell. En altres paraules, la seva paritat (la qualitat de parell o senar) és parella. La mane...».
(Cap diferència)

Revisió del 03:00, 19 des 2014

El nombre zero (0) és parell. En altres paraules, la seva paritat (la qualitat de parell o senar) és parella. La manera més senzilla de demostrar-ho és recórrer a la definició de "parell": un nombre enter múltiple de dos (2); concretament, {{{1}}}. En conseqüència, el zero té totes les propietats que tenen la resta de nombres parells: és divisible per 2, té un nombre senar a cada costat de la recta numèrica, constitueix la suma d'un enter amb si mateix (en aquest cas ell mateix), i un conjunt de 0 objectes es pot dividir en dos subconjunts iguals.

El zero també compleix els patrons que formen els nombres parells. Perquè es compleixin les regles de paritat de l'aritmètica, per exemple que {{{1}}} és necessari que 0 sigui parell. El zero també és l'element identitat del grup d'enters parells i és el punt de partida des del qual els altres nombres naturals són definits inductivament. Les aplicacions d'aquesta inducció, des de la teoria de grafs fins a la geometria computacional, es basen en la paritat parella del zero. El 0 no és únicament divisible per 2, sinó per tots els enters positius. En el sistema binari que fan servir els ordinadors, és especialment rellevant que el 0 sigui divisible per cada potència de 2; en aquest sentit, el 0 és el nombre "més parell" de tots.

Entre el públic general, la paritat del zero es presta a confusió. La majoria de gent acostuma a ser més lenta classificant el 0 com a parell que no pas per fer-ho amb els nombres 2, 4, 6 o 8, per exemple. Alguns estudiants de matemàtiques, i fins i tot alguns professors, creuen que el zero és senar, parell i senar simultàniament o ni una cosa ni l'altra. Els investigadors en educació matemàtica creuen que aquestes confusions poden servir com a oportunitats d'aprenentatge. Estudiar igualtats com {{{1}}} pot resoldre els dubtes dels estudiants sobre si el 0 és un nombre i els seus usos en l'aritmètica. Els debats a classe poden conduir els estudiants a apreciar els principis bàsics del raonament matemàtic, com per exemple la importància de les definicions. Avaluar la paritat d'aquest nombre excepcional és un exemple primerenc d'un tema omnipresent a les matemàtiques: l'abstracció d'un concepte familiar en un marc no familiar.

Per què el zero és parell

La definició estàndard de "nombre parell" es pot fer servir per demostrar que el zero és parell. Es diu que un nombre és "parell" si és un enter múltiple de 2. Per exemple, el 10 és parell ja que equival a 5 × 2. De la mateixa manera, el zero equival a 0 × 2, per la qual cosa és parell.[1]

També es pot explicar per què el zero és parell sense recórrer a definicions formals.[2] Les explicacions a continuació dónen a entendre per què el zero és parell fent servir conceptes numèrics fonamentals. Des d'aquests fonaments, es pot racionalitzar la mateixa definició –i la seva aplicabilitat al zero.

Explicacions bàsiques

La capsa amb 0 objectes no té cap objecte vermell desaparellat.

El zero és un nombre, i els nombres es fan servir per comptar. Donat un conjunt d'objectes, s'empra un nombre per descriure quants d'objectes hi ha al conjunt. El 0 descriu un conjunt sense objectes; dit de manera més formal, és el nombre d'objectes d'un conjunt buit. El concepte de paritat s'utilitza per fer grups de dos objectes. Si els objectes d'un conjunt es poden distribuir en grups de dos, sense que no en sobri cap, llavors el nombre d'objectes és parell. Si sobra un objecte, llavors el nombre d'objectes és senar. El conjunt buit inclou zero grups de dos i no sobra cap objecte, per la qual cosa el zero és parell.

Aquestes idees es poden il·lustrar dibuixant els objectes en parelles. És difícil representar zero grups de dos, o emfatitzar la inexistència d'un objecte sobrant, per la qual cosa és útil dibuixar altres grups i comparar-los amb el zero. Per exemple, al grup de cinc objectes hi ha dues parelles i, més important, hi ha un objecte desaparellat, així doncs el 5 és senar. Al grup de quatre objectes no hi ha cap objecte desaparellat, així doncs el 4 és parell. Al grup d'un sol objecte no hi parelles i hi ha un objecte restant, així doncs l'1 és senar. Al grup de zero objectes no hi ha objecte restant, així doncs el 0 és parell.[3]

Hi ha una altra definició concreta de la qualitat de parell: si els objectes d'un conjunt es poden col·locar en dos grups de mida igual, llavors el nombre d'objectes és parell. Aquesta definició és equivalent a la primera. De nou, el zero és parell perquè el conjunt buit es pot dividir en dos grups de zero element cada un.[4]

Els nombres també es poden visualitzar com a punts d'una recta numèrica. Quan es distingeixen els nombres parells i senars, el patró esdevé obvi, especialment si s'hi inclouen els nombres imparells:

Integers −4 through 10; even numbers are open circles; odd numbers are dots

Els nombres parells i senars s'alternen. Començant des de qualsevol nombre parell, comptant de dos en dos en qualsevol direcció s'obtenen altres nombres parells; no hi ha motiu per saltar-se el zero.[5]

Amb l'introducció de la multiplicació, la paritat es pot enfocar de manera més formal emprant expressions aritmètiques. Cada enter s'obté amb (2 × ▢) + 0 o bé amb (2 × ▢) + 1; en el primer cas el nombre és parell i en el segon és senar. Per exemple, l'1 és senar perquè 1 = (2 × 0) + 1, i el 0 és parell perquè 0 = (2 × 0) + 0. Si es fa una taula partint d'aquests fets es reforça la imatge de la línia numèrica anterior.[6]

Definint "paritat"

La definició precisa d'un concepte matemàtic, com ara que "parell" vulgui dir "enter múltiple de dos", és en efecte una convenció. A diferència de "parell", alguns conceptes matemàtiques es construeixen amb el propòsit d'excloure casos trivials o degenerats. Els nombres primers en són un cas famós. Abans del segle XX, les definicions de primeritat eren inconsistents, i alguns matemàtics significatius com Goldbach, Lambert, Legendre, Cayley i Kronecker escrigueren que l'1 era primer.[7] La definició moderna de "nombre primer" és "enter positiu amb exactament dos factors", per la qual cosa s'exclou el nombre 1. Aquesta definició es pot racionalitzar observant que encaixa de forma més natural amb els teoremes matemàtics que involucren els primers. Per exemple, el teorema fonamental de l'aritmètica és més fàcil d'exposar si l'1 no es considera primer.[8]

Seria possible redefinir el terme "parell" de forma similar perquè exclogués el zero. No obstant, en aquest cas la nova definició dificultaria més exposar els teoremes que involucren els parells. L'efecte ja es pot observar a les regles algebraiques que governen els nombres parells i senars.[9] Les regles més rellevants impliquen la suma, la resta i la multiplicació:

parell ± parell = parell
senar ± senar = parell
parell × enter = parell

Inserint valors apropiats a l'esquerra de les regles anteriors, es pot obtenir un 0 a la dreta:

2 − 2 = 0
−3 + 3 = 0
4 × 0 = 0

Les regles de més amunt serien incorrectes si el zero no fos parell.[9] En el millor dels casos haurien de ser modificades. Per exemple, un The above rules would therefore be incorrect if zero were not even. At best they would have to be modified. For example, one test study guide asserts that even numbers are characterized as integer multiples of two, but zero is "neither even nor odd".[10] Accordingly, the guide's rules for even and odd numbers contain exceptions:

even ± even = even (or zero)
odd ± odd = even (or zero)
even × nonzero integer = even[10]

Exceptuar el zero a la definició de nombre parell obliga a fer excepcions fonamentals a les regles dels nombres parells. Des d'una altra perspectiva, prenent les regles obeïdes pels parells positius requereix que el zero sigui un nombre parell perquè es continuïn complint.[9]

Contexts matemàtics

Incomptables resultats de la teoria de nombres invoquen el teorema fonamental de l'aritmètica i les propietats algebraiques dels nombres parells, per tant les decisions preses anteriorment tenen conseqüències vastes. Per exemple, el fet que els nombres positius tenguin una factorització única vol dir que es pot determinar si un nombre té un nombre parell o senar de factors primers diferents. Com que l'1 no és primer ni té factors primers, és un producte de 0 primers diferents; com que el 0 és un nombre parell, l'1 té un nombre parell de factors primers distints. Això implica que la funció de Möbius pren el valor μ(1) = 1, la qual cosa és necessària perquè sigui una funció multiplicativa i perquè funcioni la fórmula d'inversió de Möbius.[11]

No ser senar

Un nombre n és senar si existeix un enter k tal que n = 2k + 1. Una manera de demostrar que el zero no és senar és per reducció a l'absurd: si 0 = 2k + 1 llavors k = −1/2, que no és un enter.[12] Com que el zero no és senar, si es demostra que un nombre desconegut és senar, llavors aquest no pot ser zero. Aquesta observació aparentment trivial pot proveir una demostració conveninent i reveladora que expliqui per què un nombre no és zero.

Un resultat clàssic de la teoria de grafs expressa que un graf d'ordre senar sempre té almenys un vèrtex parell. (Aquesta afirmació requereix que el zero sigui parell: un graf buit té un ordre parell i un vèrtex isolat és parell.)[13] Per demostrar la constatació, és més senzill demostrar un resultat més fort: qualsevol graf d'ordre senar té un "nombre senar" de vèrtexs parells. L'aparició d'aquest nombre senar s'explica amb un resultat encara més general, conegut com el lema de l'encaix de mans: qualsevol graf té un nombre parell de vèrtexs de grau senar.[14] Finalment, el nombre parell de vèrtexs senars s'explica de forma natural amb la fórmula per sumar graus.

El lema de Sperner és una aplicació més avançada de la mateixa estratègia. El lema afirma que un cert tipus de coloració a la triangulació d'un símplex té un subsímplex que conté tots els colors. En lloc de construir directament tal subsímplex, és més convenient demostrar que existeix un nombre senar de subsímplexs a través del mètode d'inducció.[15] Una constatació més forta del lema explica per què aquest nombre és senar: naturalment es trenca com (n + 1) + n quan es prenen en consideració les dues orientacions possibles d'un símplex.[16]

Alternació parell-senar

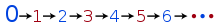
0->1->2->3->4->5->6->... in alternating colors
Definició inductiva de la paritat dels nombres naturals

El fet que el zero sigui parell, juntament amb el fet que els nombres parells i senars s'alternen, és suficient per determinar la paritat de la resta de nombres naturals. Aquesta idea es pot formalitzar en una definició inductiva del conjunt de nombres naturals parells:

  • El 0 és parell.
  • (n + 1) és parell si i només si n no és parell.

Aquesta definició té l'avantatge conceptual de basar-se només en les fundacions mínimes dels nombres naturals: l'existència del 0 i de successors. Com a tal, és útil pels sistemes lògics informàtics com LF i el demostrador de teoremes Isabelle.[17] Amb aquesta definició, la paritat del zero no és un teorema sinó un axioma. En efecte, "zero és un nombre parell" es pot interpretar com un dels axiomes de Peano, dels quals els naturals parells en són un model.[18] Una construcció similar estén la definició de paritat als ordinals transfinits: cada ordinal límit és parell, inclòs el zero, i els ordinals successors dels ordinals parells són senars.[19]

Non-convex polygon penetrated by an arrow, labeled 0 on the outside, 1 on the inside, 2 on the outside, etc.
Problema del punt al polígon

El clàssic problema del punt al polígon de la geometria computacional aplica les idees exposades més amunt. Per determinar si un punt està contingut dins d'un polígon, es traça una semirecta des de l'infinit fins al punt i es compten el nombre de vegades que la recta es creua una aresta del polígon. Aquest nombre serà parell si i només si el punt està fora del polígon. Aquest algorisme funciona perquè si el raig mai no interseca amb el polígon, llavors el nombre d'interseccions serà zero, que és parell, i el punt serà a l'exterior. Cada vegada que la recta es creua amb el polígon, el nombre d'encreuaments alterna entre parell i senar, i el punt d'intersecció alterna entre l'interior i l'exterior.[20]

A graph with 9 vertices, alternating colors, labeled by distance from the vertex on the left
Construint una bipartició

En teoria de grafs, un graf bipartit és un graf els vèrtexs dels quals es divideix en dos colors, de tal manera que els vèrtexs contigus tenen colors diferents. Si un graf connectat no té cicles senars, llavors es pot construir una bipartició elegint un vèrtex base v i acolorint cada vèrtex de negre o de blanc, depenent de si la seva distància del vèrtex v és parella o senar. Com que la distància entre v i ell mateix és 0 i el 0 és parell, el vèrtex base té un color diferent dels seus vèrtexs contigus, que es troben a una distància 1.[21]

Patrons algebraics

Integers −4 through +4 arranged in a corkscrew, with a straight line running through the evens
2Z (blau) com a subgrup de Z

En àlgebra abstracta, els enters parells formen diverses estructures algebraiques que requereixen la inclusió del zero. El fet que l'element neutre de la suma (0) sigui parell, afegit a la qualitat de parell de les sumes i els oposats dels nombres parells i a l'associativitat de la suma, implica que els enters parells formen un grup. A més a més, el grup d'enters parells amb la suma és un subgrup del grup de tots els enters; aquest és un exemple elemental del concepte de subgrup.[13] L'observació esmentada anteriorment de que "parell – parell = parell" obliga al 0 a ser parell és part d'un patró general: qualsevol conjunt no buit d'un grup suma que està tancat baix la resta ha de ser un subgrup i, particularment, ha de contenir l'element neutre.[22]

En vista que els enters parells formen un subgrup dels enters, parteixen els enters en classes laterals. Aquestes classes laterals es poden descriure com les classes d'equivalència de la següent relació d'equivalència: x ~ y si (x − y) és parell. Aquí, la qualitat de parell del zero es manifesta directament com la reflexivitat de la relació binària ~.[23] Només hi ha dues classes laterals d'aquest subgrup –els nombre parells i senars– per la qual cosa té índex 2.

Anàlogament, el grup alternant és un subgrup d'índex 2 a dins del grup simètric de n lletres. Els elements del grup alternant, anomenats permutacions parelles, són els productes dels nombres parells de les transposicions. La funció identitat, un producte buit de cap transposició, és una permutació parella donat que el zero és parell; és l'element identitat del grup.[24]

La regla "parell × enter = parell" suposa que els nombres parells formen un ideal a l'anell dels enters, i la relació d'equivalència esmentada es pot descriure com equivalència mòdul aquest ideal. Particularment, els enters parells són exactament aquells enters k que k ≡ 0 (mod 2). Aquesta formulació resulta útil per trobar les arrels d'un polinomi.[25]

Ordre 2-àdic

En un cert sentit hi ha múltiples de 2 que són "més parells" que d'altres. Els múltiples de 4 s'anomenen dobles parells, ja que es poden dividir per 2 dues vegades. En el cas del zero, no només és divisible per 4, sinó que té la propietat exclusiva de ser divisible per tota potència de 2, essent així el nombre "més parell" de tots.[26]

Una conseqüència d'aquest fet es manifesta a l'ordenament dels bits inversos dels tipus de dada integer, que utilitzen alguns algorismes d'ordinador com el de Cooley-Tukey a la Transformada Ràpida de Fourier. Aquest ordenament té la propietat que com més a l'esquerra es troba el primer 1 de l'expansió binària d'un nombre (o dit d'altra manera, com més vegades aquest es pot dividir per 2), abans se situa el nombre en l'ordenament. La inversió de 0 segueix sent 0; aquest es pot dividir per 2 tantes vegades com es vulgui i la seva expansió binària no conté cap 1, per la qual cosa sempre va en la primera posició.[27]

Encara que el 0 és divisible per 2 més vegades que qualsevol altre nombre, no és senzill quantificar exactament quantes vegades es pot fer. Per qualsevol enter diferent de zero n, es pot definir l'ordre 2-àdic de n com el nombre de vegades que és divisible per 2. Aquesta definició no funciona pel 0; per moltes vegades que sigui dividit per 2, sempre es pot tornar a fer. Per això, la convenció habitual és establir que el 2-ordre de 0 és infinit com a cas especial.[28] Aquesta convenció no és exclusiva del 2-ordre; és un dels axiomes d'una valuació d'una suma en àlgebra superior.[29]

Les potències de dos –1, 2, 4, 8, ...– formen una seqüència simple de nombres de 2-ordre creixent. En el cas dels nombres 2-àdics, aquestes seqüències convergeixen cap a zero.[30]

Referències

Citacions

  1. ↑ Penner 1999, p. 34: Lemma B.2.2, The integer 0 is even and is not odd. Penner uses the mathematical symbol ∃, the existential quantifier, to state the proof: "To see that 0 is even, we must prove that ∃k (0 = 2k), and this follows from the equality 0 = 2 ⋅ 0."
  2. ↑ Ball, Lewis & Thames (2008, p. 15) discuss this challenge for the elementary-grades teacher, who wants to give mathematical reasons for mathematical facts, but whose students neither use the same definition, nor would understand it if it were introduced.
  3. ↑ Lichtenberg 1972, pàg. 535–536 "Zero groups of two stars are circled. No stars are left. Therefore, zero is an even number."
  4. ↑ Dickerson i Pitman, 2012, p. 191.
  5. ↑ Lichtenberg 1972, p. 537; compare her Fig. 3. "If the even numbers are identified in some special way ... there is no reason at all to omit zero from the pattern."
  6. ↑ Lichtenberg 1972, pàg. 537–538 "At a more advanced level ... numbers expressed as (2 × ▢) + 0 are even numbers ... zero fits nicely into this pattern."
  7. ↑ Caldwell i Xiong, 2012, p. 5–6.
  8. ↑ Gowers 2002, p. 118 "The seemingly arbitrary exclusion of 1 from the definition of a prime … does not express some deep fact about numbers: it just happens to be a useful convention, adopted so there is only one way of factorizing any given number into primes." For a more detailed discussion, see Caldwell & Xiong (2012).
  9. ↑ 9,0 9,1 9,2 Partee 1978, p. xxi
  10. ↑ 10,0 10,1 Stewart 2001, p. 54 These rules are given, but they are not quoted verbatim.
  11. ↑ Devlin 1985, pàg. 30–33
  12. ↑ Penner, 1999, p. 34.
  13. ↑ 13,0 13,1 Berlinghoff, Grant & Skrien 2001 For isolated vertices see p. 149; for groups see p. 311.
  14. ↑ Lovász, Pelikán & Vesztergombi 2003, pàg. 127–128
  15. ↑ Starr 1997, pàg. 58–62
  16. ↑ Border 1985, pàg. 23–25
  17. ↑ Lorentz 1994, pàg. 5–6; Lovas & Pfenning 2008, p. 115; Nipkow, Paulson & Wenzel 2002, p. 127
  18. ↑ Bunch 1982, p. 165
  19. ↑ Salzmann et al. 2007, p. 168
  20. ↑ Wise 2002, pàg. 66–67
  21. ↑ Anderson 2001, p. 53; Hartsfield & Ringel 2003, p. 28
  22. ↑ Dummit & Foote 1999, p. 48
  23. ↑ Andrews 1990, p. 100
  24. ↑ Tabachnikova & Smith 2000, p. 99; Anderson & Feil 2005, pàg. 437–438
  25. ↑ Barbeau 2003, p. 98
  26. ↑ Arnold 1919, p. 21 "By the same test zero surpasses all numbers in 'evenness.'"; Wong 1997, p. 479 "Thus, the integer b000⋯000 = 0 is the most 'even.'
  27. ↑ Wong 1997, p. 479
  28. ↑ Gouvêa 1997, p. 25 Of a general prime p: "The reasoning here is that we can certainly divide 0 by p, and the answer is 0, which we can divide by p, and the answer is 0, which we can divide by p…" (ellipsis in original)
  29. ↑ Krantz 2001, p. 4
  30. ↑ Salzmann et al. 2007, p. 224

Bibliografia

Aquest article o secció s'està elaborant i està inacabat. Un viquipedista hi està treballant i és possible que trobeu defectes de contingut o de forma. Comenteu abans els canvis majors per coordinar-los. Aquest avís és temporal: es pot treure o substituir per {{incomplet}} després d'uns dies d'inactivitat.
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Paritat_del_zero&oldid=14515354»