Conjectura de Collatz

Graf dirigit que mostra les òrbites de nombres petits sota el mapa de Collatz, saltant els nombres parells. La conjectura de Collatz afirma que tots els camins eventualment porten cap a 1.

La conjectura de Collatz és un dels problemes no resolts més famosos de les matemàtiques. La conjectura es pregunta si repetir dues operacions aritmètiques simples acabarà transformant cada nombre enter positiu en 1.

Es tracta de seqüències de nombres enters en què cada terme s'obté del terme anterior de la següent manera: si el terme anterior és parell, el terme següent és la meitat del terme anterior. Si el terme anterior és senar, el següent és 3 vegades el terme anterior més 1. La conjectura és que aquestes seqüències sempre arriben a 1, independentment del nombre enter positiu que s'esculli per iniciar la seqüència.

Aquesta conjectura porta el nom del matemàtic Lothar Collatz, que va presentar la idea l'any 1937, dos anys després de doctorar-se. També es coneix com el problema 3n + 1, la conjectura 3n + 1, la conjectura d'Ulam (per Stanisław Ulam), el problema de Kakutani (per Shizuo Kakutani), la conjectura de Thwaites (per Sir Bryan Thwaites), l'algoritme de Hasse (per Helmut Hasse), o el problema de Syracuse (per la Universitat americana de Syracuse que hi va dedicar molts esforços).

La seqüència de números implicada de vegades es coneix com a seqüència de calamarsa, números de calamarsa o númerals de calamarsa (perquè els valors solen estar subjectes a múltiples baixades i ascensos com la calamarsa en un núvol), o com a nombres meravellosos.

Paul Erdős va dir sobre la conjectura de Collatz: «Les matemàtiques potser no estan preparades per a aquests problemes». També va oferir 500 US$ per la seva solució. Jeffrey Lagarias va afirmar el 2010 que la conjectura de Collatz «és un problema extraordinàriament difícil, completament fora de l'abast de les matemàtiques actuals».

Enunciat del problema

Considerem la següent operació sobre un nombre enter positiu arbitrari:

• Si el nombre és parell, dividir-lo per dos.
• Si el nombre és senar, triplicar-lo i afegeix-ne un.

En notació aritmètica modular, definim la funció ƒ de la següent manera:

$f(n)={\begin{cases}{\frac {n}{2}}&{\text{si }}n\equiv 0{\pmod {2}}\\[4px]3n+1&{\text{si }}n\equiv 1{\pmod {2}}.\end{cases}}$

Ara formem una seqüència realitzant aquesta operació repetidament, començant per qualsevol nombre enter positiu i prenent el resultat a cada pas com a entrada al següent.

En notació:

$a_{i}={\begin{cases}n&{\text{per a }}i=0\\f(a_{i-1})&{\text{per a }}i>0\end{cases}}$

(és a dir: a_i és el valor de ƒ aplicat a n recursivament i vegades; a_i = ƒⁱ (n)

La conjectura de Collatz diu: «aquest procés arribarà finalment al número 1, independentment de quin enter positiu es tria inicialment».

• 
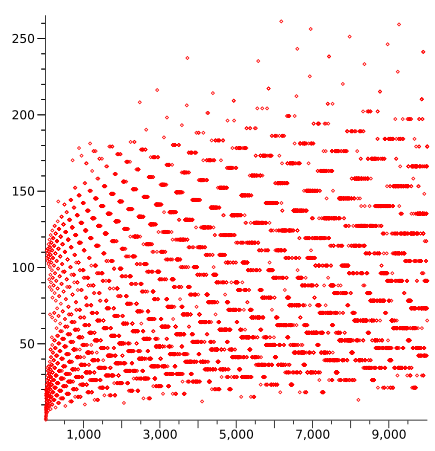
  Nombres de l'1 al 9999 i el seu corresponent temps total d'aturada
• 
  Temps total d'aturada dels números fins a 250, 1.000, 4.000, 20.000, 100.000, 500.000

Si la conjectura és falsa, només pot ser perquè hi ha algun número inicial que dóna lloc a una seqüència que no conté 1. Aquesta seqüència entraria en un cicle repetitiu que exclou l'1 o augmentaria sense límit. Encara no s'ha trobat aquesta seqüència.

• 
  Temps d'iteració per a les entrades de 2 fins a 10⁷
• 
  Temps d'iteració per a les entrades de 2 fins a 10⁸

La i més petita tal que a_i < a₀ s'anomena temps d'aturada de n. De la mateixa manera, el k més petit tal que a_k = 1 s'anomena temps d'aturada total de n. Si un dels índexs i o k no existeix, diem que el temps d'aturada o el temps d'aturada total, respectivament, és infinit.

La conjectura de Collatz afirma que el temps total d'aturada de cada n és finit. També equival a dir que cada n ≥ 2 té un temps d'aturada finit.

• 
  Histograma dels temps totals d'aturada per als números de l'1 al 10⁸. El temps total d'aturada es troba a l'eix x, la freqüència a l'eix y
• 
  Histograma dels temps totals d'aturada per als números de l'1 al 10⁹. El temps total d'aturada es troba a l'eix x, la freqüència a l'eix y

Com que 3n + 1 és parell sempre que n és senar, es pot utilitzar la forma «drecera» de la funció de Collatz:

$f(n)={\begin{cases}{\frac {n}{2}}&{\text{si }}n\equiv 0{\pmod {2}},\\[4px]{\frac {3n+1}{2}}&{\text{si }}n\equiv 1{\pmod {2}}.\end{cases}}$

Aquesta definició produeix valors més petits per al temps d'aturada i el temps d'aturada total sense canviar la dinàmica global del procés.

Dades empíriques

Per exemple, començant per n = 12 i aplicant la funció ƒ sense «drecera» s'obté la seqüència 12, 6, 3, 10, 5, 16, 8, 4, 2, 1.

El nombre n = 19 triga més a arribar a 1: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

La seqüència per a n = 27, enumerada i representada gràficament a continuació, fa 111 passos (41 passos a través de nombres senars, en negreta), pujant fins a 9232 abans de baixar a 1).

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 (successió A008884 a l'OEIS)

• 

Els nombres amb un temps d'aturada total més llarg que el de qualsevol valor inicial més petit formen una seqüència que comença amb:

1, 2, 3, 6, 7, 9, 18, 25, 27, 54, 73, 97, 129, 171, 231, 313, 327, 649, 703, 871, 1161, 2223, 2463, 2919, 3711, 6171, ... (successió A006877 a l'OEIS).

Els valors inicials el punt màxim de la trajectòria dels quals és superior al de qualsevol valor inicial més petit són els següents:

1, 2, 3, 7, 15, 27, 255, 447, 639, 703, 1819, 4255, 4591, 9663, 20895, 26623, 31911, 60975, 77671, 113383, 138367, 159487, 270271, 665215, 704511, ... (successió A006884 a l'OEIS)

Nombre de passos perquè n arribi a 1 són

0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, ... (successió A006577 a l'OEIS)

El valor inicial que té el temps d'aturada total més gran mentre està

menor que 10 és 9, que té 19 passos,

menor que 100 és 97, que té 118 passos,

menor que 1000 és 871, que té 178 passos,

menor que 10⁴ és 6171, que té 261 passos,

menor que 10⁵ és 77.031, que té 350 passos,

menor que 10⁶ és 837.799, que té 524 passos,

menor que 10⁷ és 8.400.511, que té 685 passos,

menor que 10⁸ és 63.728.127, que té 949 passos,

menor que 10⁹ és 670.617.279, que té 986 passos,

menor que 10¹⁰ és 9.780.657.630, que té 1132 passos,

menor que 10¹¹ és 75.128.138.247, que té 1228 passos,

menor que 10¹² és 989.345.275.647, que té 1348 passos.

Aquests números són els més baixos amb el recompte de passos indicat, però no necessàriament els únics per sota del límit donat. Per exemple, 9.780.657.631 té 1132 passos, igual que 9.780.657.630.

Els valors inicials que tenen el temps d'aturada total més petit respecte al seu nombre de dígits (en base 2) són les potències de dos, ja que 2ⁿ es redueix a la meitat n vegades per arribar a 1, i mai s'incrementa.

Visualizations

• 
  Graf dirigit que mostra les òrbites dels primers 1000 nombres
• 
  L'eix x representa el nombre inicial, l'eix y representa el nombre més alt assolit durant la cadena fins a 1. Aquest gràfic mostra un eix y restringit: alguns valors x produeixen intermedis fins a 2,7×10⁷ (per a x = 9663)
• 
  El mateix gràfic a l'esquerra però a escala logarítmica, de manera que es mostren tots els valors y. La primera línia gruixuda cap a la meitat de la parcel·la correspon a la punta a 27, que arriba al màxim a 4616
• 
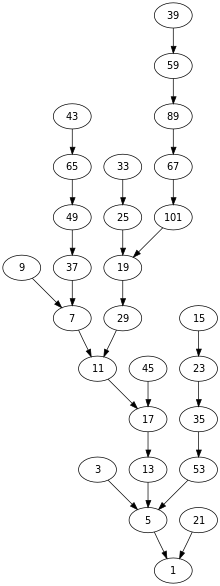
  L'arbre de tots els nombres que tenen menys de 20 passos.

Arguments de suport

Tot i que la conjectura no s'ha demostrat, la majoria dels matemàtics que han estudiat el problema creuen que la conjectura és certa perquè l'evidència experimental i els arguments heurístics els donen suport.

Evidència experimental

A partir del 2020, la conjectura s'ha verificat per ordinador per a tots els valors inicials fins a 2⁶⁸ ≈ 2,95×10²⁰. Tots els valors inicials provats fins ara acaben en el cicle de repetició (4; 2; 1) del període 3.

Aquesta evidència informàtica no és suficient per demostrar que la conjectura és certa per a tots els valors inicials. Com en el cas d'algunes conjectures refutades, com la conjectura de Pólya, es podrien trobar contraexemples quan es consideren nombres molt grans.

Tanmateix, aquestes verificacions poden tenir altres implicacions. Per exemple, es poden derivar restriccions addicionals sobre el període i la forma estructural d'un cicle no trivial.

Una heurística probabilística

Si només es tenen en compte els nombres senars de la seqüència generada pel procés de Collatz, llavors cada nombre senar és de mitjana 3/4 de l'anterior (més precisament, la mitjana geomètrica de les proporcions dels resultats és 3/4). Això produeix un argument heurístic que cada seqüència de calamarsa hauria de disminuir a llarg termini, encara que això no és una evidència contra altres cicles, només contra la divergència. L'argument no és una prova perquè suposa que les seqüències de calamarsa es munten a partir d'esdeveniments probabilístics no correlacionats (s'estableix rigorosament que l'extensió de 2-àdic del procés de Collatz té dos passos de divisió per a cada pas de multiplicació per a gairebé tots els valors inicials de 2-àdic.)

Temps d'aturada

Com ha demostrat Riho Terras, gairebé tots els nombres enters positius tenen un temps d'aturada finit. En altres paraules, gairebé totes les seqüències de Collatz arriben a un punt estrictament per sota del seu valor inicial. La demostració es basa en la distribució de vectors de paritat i utilitza el teorema del límit central.

El 2019, Terence Tao va millorar aquest resultat mostrant, utilitzant la densitat logarítmica, que gairebé totes les òrbites de Collatz baixen per sota de qualsevol funció determinada del punt de partida, sempre que aquesta funció divergeixi fins a l'infinit, per molt lentament que sigui. En resposta a aquest treball, Quanta Magazine va escriure que Tao «va obtenir un dels resultats més significatius sobre la conjectura de Collatz en dècades».

Límits inferiors

En una proba assistida per ordinador, Krasikov i Lagarias van demostrar que el nombre de nombres enters de l'interval [1,x] que finalment arriben a 1 és almenys igual a x^0.84 per a tots els x prou grans.

Cicles

En aquesta part, considerem la forma de drecera de la funció de Collatz

$f(n)={\begin{cases}{\frac {n}{2}}&{\text{si }}n\equiv 0{\pmod {2}},\\[4px]{\frac {3n+1}{2}}&{\text{si }}n\equiv 1{\pmod {2}}.\end{cases}}$

Un cicle és una seqüència (a₀, a₁, ..., a_q) de diferents nombres enters positius on ƒ(a₀) = a₁, ƒ(a₁) = a₂, ..., i ƒ(a_q) = a₀.

L'únic cicle conegut és (1,2) del període 2, anomenat cicle trivial.

Llargada del cicle

Se sap que la llargada d'un cicle no trivial és d'almenys 17.087.915. De fet, [Eliahou 1993] va demostrar que el període p de qualsevol cicle no trivial és de la forma

$p=301994a+17087915b+85137581c$

on a, b i c són nombres enters no negatius, b ≥ 1 i ac = 0. Aquest resultat es basa en l'expansió de la fracció contínua ln 3/ln 2.

k-cicles

Un k-cicle és un cicle que es pot dividir en 2k subseqüències contigües: k seqüències creixents de nombres senars alternant amb k seqüències decreixents de nombres parells. Per exemple, si el cicle consisteix en una única seqüència creixent de nombres senars seguida d'una seqüència decreixent de nombres parells, s'anomena 1-cicle.

[Steiner 1977] va demostrar que no hi ha un cicle més que el trivial (1; 2). [Simons 2005] va utilitzar el mètode de Steiner per demostrar que no hi ha 2-cicles. [Simons i de Weger 2005] van ampliar aquesta demostració fins a 68-cicles; no hi ha k-cicles fins a k = 68. Per a cada k més enllà de 68, aquest mètode dóna un límit superior per al terme més petit d'un k-cicle; per exemple, si hi ha un 77-cicle, almenys un element del cicle és inferior a 38137×2⁵⁰. Juntament amb la verificació de la conjectura fins a 2⁶⁸, això implica la inexistència d'un k-cicle no trivial fins a k = 77. A mesura que continuen les cerques exhaustives per ordinador, es poden descartar valors de k més grans. Per afirmar l'argument de manera més intuïtiva: no cal buscar cicles que tinguin com a màxim 77 circuits, on cada circuit consta de pujades consecutives seguits de baixades consecutives.

Altres formulacions de la conjectura

A l'invers

Hi ha un altre enfocament per demostrar la conjectura, que considera el mètode de baix a dalt per fer créixer l'anomenat graf de Collatz. El graf de Collatz és un graf definit per la relació inversa

$R(n)={\begin{cases}\{2n\}&{\text{si }}n\equiv 0,1,2,3,5\\[4px]\left\{2n,{\frac {n-1}{3}}\right\}&{\text{si }}n\equiv 4\end{cases}}{\pmod {6}}.$

• 
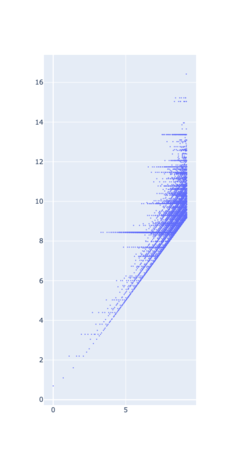
  Els primers 21 nivells del graf de Collatz generats de manera ascendent. El graf inclou tots els números amb una longitud d'òrbita de 21 o menys

Per tant, en comptes de demostrar que tots els nombres enters positius eventualment condueixen a 1, podem provar de demostrar que 1 condueix cap enrere a tots els enters positius. Per a qualsevol nombre enter n, n ≡ 1 (mod 2) si i només si 3n + 1 ≡ 4 (mod 6). De manera equivalent, n − 1/3 ≡ 1 (mod 2) si i només si n ≡ 4 (mod 6). Conjecturalment, aquesta relació inversa forma un arbre excepte per al bucle 1–2–4 (la inversa del bucle 4–2–1 de la funció inalterada f definida a la secció Enunciat del problema d'aquest article).

Quan la relació 3n + 1 de la funció ƒ es substitueix per la relació «drecera» substitutiva comuna 3n + 1/2, el graf de Collatz es defineix per la relació inversa,

$R(n)={\begin{cases}\{2n\}&{\text{si }}n\equiv 0,1\\[4px]\left\{2n,{\frac {2n-1}{3}}\right\}&{\text{si }}n\equiv 2\end{cases}}{\pmod {3}}.$

Per a qualsevol nombre enter n, n ≡ 1 (mod 2) si i només si 3n + 1/2 ≡ 2 (mod 3). De manera equivalent, 2n − 1/3 ≡ 1 (mod 2) si i només si n ≡ 2 (mod 3). Conjecturalment, aquesta relació inversa forma un arbre excepte per a un bucle 1–2 (la inversa del bucle 1–2 de la funció ƒ(n) revisada com s'ha indicat anteriorment).

Alternativament, substituïm el 3n + 1 per n′/H(n′)  on n′ = 3n + 1 i H(n′) és la potència de 2 més alta que divideix n′ (sense residu). La funció resultant ƒ mapeja de nombres senars a nombres senars. Ara suposem que per a un nombre senar n, aplicant aquesta operació k vegades, es produeix el nombre 1 (és a dir, ƒ^k(n) = 1). Aleshores, en binari, el nombre n es pot escriure com la concatenació de cadenes w_k w_k−1 ... w₁ on cada w_h és un extracte finit i contigu de la representació de 1/3^h. Per tant, la representació de n té les repeticions de 1/3^h, on cada repetició es gira opcionalment i després es replica fins a un nombre finit de bits. És només en binari que això passa. Conjecturalment, es pot arribar a totes les cadenes binàries s que acaben amb un 1 mitjançant una representació d'aquesta forma (on podem afegir o suprimir els 0 a les s).

Com una màquina abstracta que calcula en base dos

Les aplicacions repetides de la funció Collatz es poden representar com una màquina abstracta que gestiona cadenes de bits. La màquina realitzarà els tres passos següents sobre qualsevol nombre senar fins que només quedi un 1:

• Afegir 1 a l'extrem (dret) del nombre en binari (donant 2n + 1);
• Afegir-ho al nombre original per suma binària (donant 2n + 1 + n = 3n + 1);
• Treure tots els 0 posteriors (és a dir, dividir-los repetidament per 2 fins que el resultat sigui senar).

Exemple

El número inicial 7 s'escriu a la base dos com 111. La seqüència de Collatz resultant és:

         111
        1111
       10110
      10111
     100010
    100011
    110100
   11011
  101000
 1011
10000

Com a seqüència de paritat

Per a aquesta secció, considerem la funció de Collatz en la forma lleugerament modificada

$f(n)={\begin{cases}{\frac {n}{2}}&{\text{si }}n\equiv 0\\[4px]{\frac {3n+1}{2}}&{\text{si }}n\equiv 1\end{cases}}{\pmod {2}}.$

Això es pot fer perquè quan n és senar, 3n + 1 sempre és parell.

Si P(...) és la paritat d'un nombre, és a dir, P(2n) = 0 i P(2n + 1) = 1, llavors podem definir la seqüència de paritat de Collatz (o vector de paritat) per a un nombre n com p_i = P(a_i), on a₀ = n, i a_i+1 = ƒ(a_i).

Quina operació es realitza, 3n + 1/2 o n/2, depèn de la paritat. La seqüència de paritat és la mateixa que la seqüència d'operacions.

Utilitzant aquesta forma per a ƒ(n), es pot demostrar que les seqüències de paritat de dos nombres m i n coincidiran en els primers k termes si i només si m i n són equivalents mòdul 2^k. Això implica que cada nombre s'identifica de manera única per la seva seqüència de paritat i, a més, si hi ha diversos cicles de calamarsa, els seus cicles de paritat corresponents han de ser diferents.

L'aplicació de la funció ƒ k vegades al nombre n = 2^ka + b donarà el resultat 3^ca + d, on d és el resultat d'aplicar la funció ƒ k vegades a b i c és el nombre d'augments que s'han trobat durant aquesta seqüència. Per exemple, per a 2⁵a + 1 hi ha 3 augments a mesura que 1 itera a 2, 1, 2, 1, i finalment a 2, de manera que el resultat és 3³a + 2; per a 2²a + 1 només hi ha 1 augment quan 1 puja a 2 i baixa a 1, de manera que el resultat és 3a + 1. Quan b és 2^k − 1, hi haurà k augments i el resultat serà 2 × 3^ka − 1. El factor de 3 que multiplica a és independent del valor d'a; només depèn del comportament de b. Això permet predir que determinades formes de nombres sempre portaran a un nombre més petit després d'un cert nombre d'iteracions: per exemple, 4a + 1 es converteix en 3a + 1 després de dues aplicacions de ƒ i 16a + 3 es converteix en 9a + 2 després de 4 aplicacions de ƒ. Però que aquests nombres més petits continuïn fins a 1 depèn del valor de a.

Com a sistema d'etiquetes

Per a la funció de Collatz en la forma

$f(n)={\begin{cases}{\frac {n}{2}}&{\text{si }}n\equiv 0\\[4px]{\frac {3n+1}{2}}&{\text{si }}n\equiv 1.\end{cases}}{\pmod {2}}$

Les seqüències de calamarsa es poden calcular mitjançant el sistema extremadament senzill de 2-etiquetes amb regles de producció

a → bc, b → a, c → aaa.

En aquest sistema, l'enter positiu n es representa amb una cadena de n còpies de a, i la iteració de l'operació d'etiqueta s'atura en qualsevol paraula de longitud inferior a 2. (Adaptat de [De Mol 2008]).

2-tag system 
    Alphabet: {a,b,c} 
    Production rules:
         a  --> bc
         b  --> a
         c  --> aaa

Computation
    Initial word: aaa <--> n=3
                    abc  
                      cbc
                        caaa
                          aaaaa  <--> 5
                            aaabc
                              abcbc
                                cbcbc
                                  cbcaaa
                                    caaaaaa
                                      aaaaaaaa  <--> 8
                                        aaaaaabc
                                          aaaabcbc
                                            aabcbcbc
                                              bcbcbcbc
                                                bcbcbca
                                                  bcbcaa
                                                    bcaaa
                                                      aaaa  <--> 4
                                                        aabc
                                                          bcbc
                                                            bca
                                                              aa  <--> 2
                                                                bc
                                                                  a  <--> 1
                                                                   (halt)

La conjectura de Collatz afirma de manera equivalent que aquest sistema d'etiquetes, amb una cadena finita arbitrària de a com a paraula inicial, finalment s'atura.

Ampliacions a dominis més grans

Iteració sobre tots els nombres enters

Una extensió de la conjectura de Collatz és incloure tots els nombres enters, no només els enters positius. Deixant de banda el cicle 0 → 0 que no es pot introduir des de l'exterior, hi ha un total de quatre cicles coneguts, en els quals tots els enters diferents de zero semblen caure eventualment sota la iteració de ƒ. Aquests cicles s'enumeren aquí, començant pel conegut cicle per a n positiu:

Els valors senars es mostren en negreta gran. Cada cicle apareix en primer lloc amb el seu membre de valor absolut mínim (que sempre és senar).

Cicle	Durada del cicle de valor imparell	Durada del cicle complet
1 → 4 → 2 → 1 ...	1	3
−1 → −2 → −1 ...	1	2
−5 → −14 → −7 → −20 → −10 → −5 ...	2	5
−17 → −50 → −25 → −74 → −37 → −110 → −55 → −164 → −82 → −41 → −122 → −61 → −182 → −91 → −272 → −136 → −68 → −34 → −17 ...	7	18

La conjectura generalitzada de Collatz és l'afirmació que cada nombre enter, sota la iteració de ƒ, finalment cau en un dels quatre cicles anteriors o el cicle 0 → 0. (El cicle 0 → 0 només s'inclou per a la completitud).

Iteració sobre racionals amb denominadors senars

El mapa de Collatz es pot estendre a nombres racionals (positius o negatius) que tenen denominadors senars quan s'escriuen en termes més baixos.

El nombre es considera «parell» o «senar» segons si el seu numerador és parell o senar. Aleshores, la fórmula del mapa és exactament la mateixa que quan el domini són els nombres enters: un racional «parell» d'aquest tipus es divideix per 2; un racional «senar» es multiplica per 3 i després s'afegeix 1. Un fet estretament relacionat és que el mapa de Collatz s'estén a l'anell de nombres enters 2-àdics, que conté l'anell de racionals amb denominadors senars com a subanell.

Quan s'utilitza la definició de «drecera» del mapa de Collatz, se sap que qualsevol seqüència de paritat periòdica és generada per exactament un racional. Per contra, es conjectura que tot racional amb un denominador senar té una seqüència de paritat eventualment cíclica (Conjectura de periodicitat).

Si un cicle de paritat té una longitud n i inclou nombres senars exactament m vegades als índexs k₀ < ⋯ < k_m−1, llavors l'únic racional que genera immediatament i periòdicament aquest cicle de paritat és

${\frac {3^{m-1}2^{k_{0}}+\cdots +3^{0}2^{k_{m-1}}}{2^{n}-3^{m}}}.$

(1)

Per exemple, el cicle de paritat (1 0 1 1 0 0 1) té una longitud de 7 i quatre termes senars als índexs 0, 2, 3 i 6. Això és generat repetidament per la fracció

${\frac {3^{3}2^{0}+3^{2}2^{2}+3^{1}2^{3}+3^{0}2^{6}}{2^{7}-3^{4}}}={\frac {151}{47}}$

ja que aquest últim condueix al cicle racional

${\frac {151}{47}}\rightarrow {\frac {250}{47}}\rightarrow {\frac {125}{47}}\rightarrow {\frac {211}{47}}\rightarrow {\frac {340}{47}}\rightarrow {\frac {170}{47}}\rightarrow {\frac {85}{47}}\rightarrow {\frac {151}{47}}.$

Qualsevol permutació cíclica de (1 0 1 1 0 0 1) s'associa a una de les fraccions anteriors. Per exemple, el cicle (0 1 1 0 0 1 1) és produït per la fracció

${\frac {3^{3}2^{1}+3^{2}2^{2}+3^{1}2^{5}+3^{0}2^{6}}{2^{7}-3^{4}}}={\frac {250}{47}}.$

Per a una correspondència un a un, un cicle de paritat hauria de ser irreductible, és a dir, no dividible en subcicles idèntics. Com a il·lustració d'això, el cicle de paritat (1 1 0 0 1 1 0 0) i el seu subcicle (1 1 0 0) estan associats a la mateixa fracció 5/7 quan es redueix als termes més baixos.

En aquest context, assumir la validesa de la conjectura de Collatz implica que (1 0) i (0 1) són els únics cicles de paritat generats per nombres enters positius (1 i 2, respectivament).

Si el denominador senar d d'un racional no és múltiple de 3, aleshores tots els iterats tenen el mateix denominador i la seqüència de numeradors es pot obtenir aplicant la generalització «3n + d» de la funció de Collatz.

$T_{d}(x)={\begin{cases}{\frac {x}{2}}&{\text{si }}x\equiv 0{\pmod {2}},\\[4px]{\frac {3x+d}{2}}&{\text{si }}x\equiv 1{\pmod {2}}.\end{cases}}$

Extensió 2-àdica

La funció

$T(x)={\begin{cases}{\frac {x}{2}}&{\text{si }}x\equiv 0{\pmod {2}}\\[4px]{\frac {3x+1}{2}}&{\text{si }}x\equiv 1{\pmod {2}}\end{cases}}$

està ben definit a l'anell $\mathbb {Z} _{2}$ de nombres enters 2-àdics, on és continu i conserva la mesura respecte a la mesura 2-àdica. A més, se sap que la seva dinàmica és ergòdica.

Definim la funció vectorial de paritat Q sobre la qual actua $\mathbb {Z} _{2}$ com

$Q(x)=\sum _{k=0}^{\infty }\left(T^{k}(x)\mod 2\right)2^{k}.$

La funció Q és una isometria 2-àdica. En conseqüència, cada seqüència de paritat infinita es produeix exactament per a un enter 2-àdic, de manera que gairebé totes les trajectòries són acícliques en $\mathbb {Z} _{2}$.

Una formulació equivalent de la conjectura de Collatz és aquesta

$Q\left(\mathbb {Z} ^{+}\right)\subset {\tfrac {1}{3}}\mathbb {Z} .$

Iteració sobre nombres reals o complexos

El mapa de Collatz (amb drecera) es pot veure com la restricció als nombres enters del mapa suau

$f(z)={\frac {1}{2}}z\cos ^{2}\left({\frac {\pi }{2}}z\right)+{\frac {3z+1}{2}}\sin ^{2}\left({\frac {\pi }{2}}z\right).$

Les iteracions d'aquest mapa a la línia real condueixen a un sistema dinàmic, investigat més endavant per Chamberland. Ell va demostrar que la conjectura no val per als nombres reals positius, ja que hi ha una infinitat de punts fixos, així com òrbites que escapen monòtonament a l'infinit. La funció ƒ té dos cicles d'atracció de període 2, (1; 2) i (1,1925...; 2,1386...). A més, es conjectura que el conjunt d'òrbites il·limitades és de mesura 0.

• 
  Diagrama de Verhulst de l'òrbita 10-5-8-4-2-1-2-1-2-1-etc. en l'extensió real del mapa de Collatz (optimitzat mitjançant la substitució "3n + 1" amb "(3n + 1)/2")
• 
  Mapa fractal de Collatz en un veïnat de la línia real

[Letherman, Schleicher i Wood 1999] van ampliar l'estudi al pla complex, on la majoria dels punts tenen òrbites que divergeixen fins a l'infinit (regió acolorida a la il·lustració superior). El límit entre la regió de color i els components negres, és a dir, el conjunt de Julia de ƒ, és un patró fractal, de vegades anomenat «fractal de Collatz».

Optimitzacions

Si n és múltiple de 4, es pot dividir directament per 4.

Motiu: inicialment és parell. Dividit per dos, encara és parell, de manera que es pot dividir per dos per segona vegada.

De manera més general, en factoritzar abans de n és possible substituir la potència de dos per 2⁰ = 1.

Motiu: si la potència de 2 en la primera factorització és major que 0, aleshores el nombre és parell, i en el punt següent tindrem la mateixa factorització amb 2 elevat a una potència inferior a 1. En repetir l'operació, s'arriba a 2⁰.

Per exemple: en comptes de 15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 (17 passos), es pot calcular 15, 46 (2¹×23), 23, 70 (2¹×35), 35, 106 (2¹×53), 53, 160 (2⁵×5), 5, 16 (2⁴), 1 (11 passos).

Si n és senar, es pot fer (3n + 1) / 2, saltant un pas.

Motiu: si n és senar, 3n també és senar (el producte de dos nombres senars sempre és senar) i 3n + 1 és parell, de manera que es pot dividir per dos.

Per exemple: 3 × 35 + 1 = 106.

3m + 1 sempre forma part de la seqüència de 4m + 1. Així, si n ≡ 1 (mod 4), n es pot convertir a (n - 1) / 4 tantes vegades com sigui possible, estalviant un pas cada vegada. El nombre obtingut, parell o senar, s'ha de convertir posteriorment en 3n + 1.

Motiu: 4m + 1 sempre és senar, de manera que es convertirà en 3 (4m + 1) + 1 = 12m + 4 = 4 (3m + 1), i es pot dividir per quatre.

Per exemple: 405 es pot convertir com a: 405 → 101 → 25 → 6 → 19. La seqüència normal de Collatz també conté 19: 405 → 1216 → 608 → 304 → 152 → 76 → 38 → 19.

L'anterior es pot utilitzar per a una nova formulació, equivalent a l'anterior, de la funció de Collatz:

$f(n)={\begin{cases}{\frac {n}{4}},&{\text{si }}n\equiv 0,\\3g(n)+1,&{\text{si }}n\equiv 1,\\{\frac {n}{2}},&{\text{si }}n\equiv 2,\\{\frac {1}{2}}(3n+1),&{\text{si }}n\equiv 3,\end{cases}}{\pmod {4}}$

$g(n)={\begin{cases}n,&{\text{si }}n\not \equiv 1,\\g({\frac {n-1}{4}}),&{\text{si }}n\equiv 1,\end{cases}}{\pmod {4}}$

Compartiment temps-espai

La secció Com a seqüència de paritat d'aquest article ofereix una manera d'accelerar la simulació de la seqüència. Per avançar k passos a cada iteració (utilitzant la funció ƒ d'aquesta secció), es divideix el nombre actual en dues parts, b (els k bits menys significatius, interpretats com un nombre enter) i a (la resta dels bits com a un nombre enter). El resultat de saltar endavant k passos es pot trobar com:

ƒ^k (2^ka + b) = 3^c(b)a + d(b).

Les matrius c (o millor 3^c) i d es calculen prèviament per a tots els nombres b de k bits possibles, on d(b) és el resultat d'aplicar la funció ƒ k vegades a b, i c(b) és el nombre de nombres senars. trobada pel camí. Per exemple, si k = 5, es pot avançar 5 passos a cada iteració separant els 5 bits menys significatius d'un nombre i utilitzant:

c(0...31) = { 0, 3, 2, 2, 2, 2, 2, 4, 1, 4, 1, 3, 2, 2, 3, 4, 1, 2, 3, 3, 1, 1, 3, 3, 2, 3, 2, 4, 3, 3, 4, 5 }

d(0...31) = { 0, 2, 1, 1, 2, 2, 2, 20, 1, 26, 1, 10, 4, 4, 13, 40, 2, 5, 17, 17, 2, 2, 20, 20, 8, 22, 8, 71, 26, 26, 80, 242 }.

Això requereix una precomputació i un emmagatzematge de 2^k per accelerar el càlcul resultant per un factor de k, un compromís espai-temps.

Restriccions modulars

Amb el propòsit especial de cercar un contraexemple a la conjectura de Collatz, aquesta precomputació condueix a una acceleració encara més important, utilitzada per Tomás Oliveira e Silva en les seves confirmacions computacionals de la conjectura de Collatz fins a grans valors de n. Si, per a alguns b i k donats, la desigualtat

ƒ^k (2^ka + b) = 3^c(b)a + d(b) < 2^ka + b

s'aplica per a tot a, aleshores el primer contraexemple, si existeix, no pot ser b mod 2^k. Per exemple, el primer contraexemple ha de ser senar perquè f(2n) = n, menor que 2n; i ha de ser 3 mod 4 perquè ƒ² (4n + 1) = 3n + 1, menor que 4n + 1. Per a cada valor inicial a que no sigui un contraexemple a la conjectura de Collatz, hi ha una k per a la qual es compleix aquesta desigualtat, per tant, comprovar la conjectura de Collatz per a un valor inicial és tan bo com comprovar una classe de congruència sencera. A mesura que k augmenta, la cerca només necessita comprovar aquells residus b que no s'eliminen per valors inferiors de k. Només sobreviu una fracció exponencialment petita dels residus. Per exemple, els únics residus supervivents mod 32 són 7, 15, 27 i 31.

Funció de Syracuse

Si k és un nombre enter senar, aleshores 3k + 1 és parell, per tant 3k + 1 = 2^ak′ amb k′ senar i a ≥ 1a. La funció de Syracuse és la funció ƒ del conjunt I d'enters senars en si mateix, per a la qual ƒ(k) = k′ (successió A075677 a l'OEIS).

Algunes propietats de la funció de Syracuse són:

• Per a tot k ∈ I, ƒ(4k + 1) = ƒ(k). (per que 3(4k + 1) + 1 = 12k + 4 = 4(3k + 1).)
• De manera més general: Per a tots p ≥ 1 i senar h, ƒ^p-1 (2^ph − 1) = 2 × 3^{p − 1}h − 1. (Aquí ƒ^p-1 és la notació d'iteració de funcions).
• For all odd h, ƒ(2h − 1) ≤ 3h − 1/2

La conjectura de Collatz és equivalent a l'enunciat que, «per a tot k en I, existeix un nombre enter n ≥ 1 de tal manera que ƒⁿ (k) = 1».

Generalitzacions indecidibles

El 1972, John Horton Conway va demostrar que una generalització natural del problema de Collatz és algorítmicament indecidible.

Concretament, es consideren les funcions de la forma

${g(n)=a_{i}n+b_{i}}\;\;,{\text{on}}\;{n\equiv i{\pmod {P}}}$

i a₀, b₀, ..., a_{P − 1}, b_{P − 1} són nombres racionals que són triats de tal manera que g(n) sempre és un nombre enter.

La funció estàndard de Collatz ve donada per P = 2, a₀ = 1/2, b₀ = 0, a₁ = 3, b₁ = 1. Conway va demostrar que el problema:

Donats g i n, la seqüència d'iteracions g^k(n) arriba a 1?

és indecidible, en representar el problema de l'aturada d'aquesta manera.

Més proper al problema de Collatz és el següent problema quantificat universalment:

Donats g i n, la seqüència d'iteracions g^k(n) arriba a 1, per a tot n > 0?

Modificar la condició d'aquesta manera pot fer que un problema sigui més difícil o més fàcil de resoldre (intuïtivament, és més difícil justificar una resposta positiva, però pot ser més fàcil justificar-ne una negativa). [Kurtz i Simon 2007] van demostrar que el problema anterior és, de fet, indecidible i encara més alt en la jerarquia aritmètica, concretament Π0
2-complet. Aquest resultat de duresa es manté fins i tot si es restringeix la classe de funcions g fixant el mòdul P a 6480.

Algorismes per calcular seqüències de Collatz

Es pot calcular fàcilment una seqüència de Collatz específica, tal com mostra l'exemple de pseudocodi següent:

function collatz(n)
  while n > 1
    if n senar
      set n to 3n + 1
    else
      set n to n / 2

O, utilitzant la recursivitat:

function collatz(n)
  if n > 1
    if n senar
      collatz(3n + 1)
    else
      collatz(n / 2)

Aquests programes acaben quan la seqüència arriba a 1, per evitar imprimir un bucle infinit de 4, 2, 1. Si la conjectura de Collatz és certa, els programes sempre acaben, sigui quin sigui el nombre enter positiu inicial.

Implementacions informàtiques

En llenguatge Python:

def collatz(x):
    while x > 1:
       if x % 2 == 0:
            x /= 2
        else:
            x = 3*x+1

En llenguatge Java:

static void collatz(int x) {
	System.out.println(x);
	if (x>1) {
		collatz((x%2==0) ? x/2 : (3*x+1));
	}
}

En llenguatge C:

void collatz(int x)
{	
	printf("%d ", x);	
	if (1 == x)
		return;
	else if (x % 2 == 0)		
		collatz(x/2);
	else
		collatz(3*x+1);
}

En llenguatge PHP:

function collatz($x){
	if($x == 1){
		return $x; 
	}else if($x % 2 == 0){
		$result = $x / 2;
		return collatz($result);
	}else{
		$result = ($x * 3) + 1;
		return collatz($result);
	}
}

En llenguatge Haskell:

collatz :: (Integral a) => a -> [a]
collatz 1 = [1]
collatz n  
    | even n =  n:collatz (n `div` 2)  
    | odd n  =  n:collatz (n*3 + 1)

En llenguatge Ruby:

def collatz(n)
  puts n
  return if n == 1
  return collatz(n*3 + 1) if n.odd?
  return collatz(n/2)
end

Nota històrica sobre els diferents noms

A principis de la dècada del 1930, Lothar Collatz, estudiant de la Universitat d'Hamburg, es va dedicar a la teoria de nombres i la teoria de grafs. Va començar amb un nombre enter positiu, li va aplicar un algorisme iteratiu, va dibuixar els grafs associats i es va fer preguntes que encara no s'havien contestat.

El matemàtic alemany Helmut Hasse, amic de Collatz, va difondre el problema, també conegut com a algorisme de Hasse o problema 3x + 1.

Com que Hasse va presentar el problema a la dècada del 1950 durant una visita a la Universitat de Syracuse (prop de Nova York), va proposar anomenar-lo el problema de Syracuse.

El matemàtic polonès Stanislaw Ulam va fer circular l'algorisme al Laboratori Nacional de Los Alamos, on va treballar durant la Segona Guerra Mundial. És per això que el problema també es coneix com el problema Ulam.

A la dècada del 1960, el matemàtic japonès Shizuo Kakutani es va tornar a interessar pel problema, de manera que la conjectura també s'anomena problema de Kakutani.

En la cultura popular

Segons el matemàtic Greg Muller, la importància d'aquesta conjectura rau en el fet que «els matemàtics sospiten que la resolució de la conjectura de Collatz obrirà nous horitzons i desenvoluparà noves i importants tècniques en teoria de nombres». Derek Jennings comenta que «la raó és que, com que és fàcil de presentar i entendre, té el potencial d'atreure els joves a les matemàtiques. Jo mateix vaig saber de la seva existència a l'institut i no vaig poder resistir el seu encant».

A la pel·lícula canadenca Incendies (2010), un estudiant graduat en matemàtiques pures explica la conjectura de Collatz a un grup d'estudiants de grau. Posa els seus estudis en suspens durant un temps per abordar algunes preguntes no resoltes sobre el passat de la seva família. Al final de la pel·lícula, la conjectura de Collatz resulta haver presagiat un descobriment inquietant i difícil que fa sobre la seva família.

The Ultimate Challenge: The 3x + 1 Problem, publicat l'any 2010 per l'American Mathematical Society i editat per Jeffrey Lagarias, és un compendi d'informació sobre la conjectura de Collatz, mètodes per abordar-la i generalitzacions. Inclou dos articles d'investigació de l'editor i cinc d'altres autors sobre la història del problema, generalitzacions, enfocaments estadístics i resultats de la teoria de la computació. També inclou reimpressions dels primers articles sobre el tema, inclòs el document de Lothar Collatz.

Bibliografia

• Andrei, Stefan; Masalagiu, Cristian «About the Collatz conjecture» (en anglès). Acta Informatica, 35, 1998. DOI: 10.1007/s002360050117.
• Barina, David «Convergence verification of the Collatz problem» (en anglès). The Journal of Supercomputing, 77(3), 2020. DOI: 10.1007/s11227-020-03368-x.
• Belaga, Edward G. Reflecting on the 3x+1 Mystery (en anglès). Universitat d'Estrasburg, 1998. 
• Belaga, Edward G.; Mignotte, Maurice «Embedding the 3x+1 Conjecture in a 3x+d Context» (en anglès). Experimental Mathematics, 7(2), 1998. DOI: 10.1080/10586458.1998.10504364.
• Belaga, Edward G.; Mignotte, Maurice. «Walking Cautiously into the Collatz Wilderness: Algorithmically, Number Theoretically, Randomly». A: Fourth Colloquium on Mathematics and Computer Science : Algorithms, Trees, Combinatorics and Probabilities (en anglès). Nancy (França): Institut Élie Cartan, 18-22 de setembre de 2006. 
• Ben-Amram, Amir M. «Mortality of iterated piecewise affine functions over the integers: Decidability and complexity» (en anglès). Computability, 1(1), 2015. DOI: 10.3233/COM-150032.
• Bernstein, Daniel J.; Lagarias, Jeffrey C. «The 3x + 1 conjugacy map» (en anglès). Canadian Journal of Mathematics, 48(6), 1996. DOI: 10.4153/CJM-1996-060-x. ISSN: 0008-414X.
• Bruschi, Mario. A generalization of the Collatz problem and conjecture (en anglès), 2008. 
• Chamberland, Marc «A continuous extension of the 3x + 1 problem to the real line» (en anglès). Dynam. Contin. Discrete Impuls Systems, 2(4), 1996.
• Conway, John H. «Unpredictable iterations» (en anglès). Proc. 1972 Number Theory Conf., Univ. Colorado, Boulder, 1972. (conferència).
• De Mol, Liesbeth «Tag systems and Collatz-like functions» (PDF) (en anglès). Theoretical Computer Science, 390(1), gener 2008, pàg. 92-101. DOI: 10.1016/j.tcs.2007.10.020.
• Eliahou, Shalom «The 3x + 1 problem: new lower bounds on nontrivial cycle lengths» (en anglès). Discrete Mathematics, 118(1), 1993. DOI: 10.1016/0012-365X(93)90052-U.
• Emmer, Michele. Imagine Math: Between Culture and Mathematics (en anglès). Springer Publishing, 2012. ISBN 978-8-847-02426-7. 
• Everest, Graham; van der Poorten, Alf; Shparlinski, Igor; Ward, Thomas. «3.4». A: Recurrence sequences (en anglès). 104. Providence, Rhode Island: American Mathematical Society, 2003 (Mathematical Surveys and Monographs). ISBN 0-8218-3387-1. 
• Garner, Lynn E. «On the Collatz 3n + 1 algorithm» (en anglès). Proceedings of the American Mathematical Society, 82(1), 1981. DOI: 10.1090/S0002-9939-1981-0603593-2. JSTOR: 2044308.
• Gasull i Embid, Armengol. Fes Matemàtiques!. Universitat Autònoma de Barcelona, 2001, p. 93 i seg.. ISBN 84-490-2260-6. 
• Guy, R. K. «Don't try to solve these problems» (en anglès). Amer. Math. Monthly, 90(1), 1983. DOI: 10.2307/2975688. JSTOR: 2975688. By this Erdos means that there aren't powerful tools for manipulating such objects.
• Guy, Richard K. «E16: The 3x+1 problem». A: Unsolved Problems in Number Theory (en anglès). Springer-Verlag, 2004. ISBN 0-387-20860-7. 
• Hofstadter, Douglas R. Gödel, Escher, Bach (en anglès). Nova York: Basic Books, 1979. ISBN 0-465-02685-0. 
• Krasikov, Ilia; Lagarias, Jeffrey C. «Bounds for the 3x + 1 problem using difference inequalities» (en anglès). Acta Arithmetica, 109(3), 2003. arXiv: math/0205002. Bibcode: 2003AcAri.109..237K. DOI: 10.4064/aa109-3-4.
• Kurtz, Stuart A.; Simon, Janos. «The undecidability of the generalized Collatz problem». A: Proceedings of the 4th International Conference on Theory and Applications of Models of Computation, TAMC 2007, held in Shanghai, China in May 2007 (en anglès), 2007. DOI 10.1007/978-3-540-72504-6_49. ISBN 978-3-540-72503-9.  Com a Collatz PDF.
• Lagarias, Jeffrey C. «The 3x + 1 problem and its generalizations» (en anglès). The American Mathematical Monthly, 92(1), 1985. DOI: 10.1080/00029890.1985.11971528. JSTOR: 2322189.
• Lagarias, Jeffrey «The set of rational cycles for the 3x+1 problem» (en anglès). Acta Arithmetica, 56(1), 1990. DOI: 10.4064/aa-56-1-33-53. ISSN: 0065-1036.
• Lagarias, Jeffrey C. The 3x + 1 problem: An annotated bibliography, II (2000-) (en anglès), 2006. 
• Lagarias, Jeffrey C. The Ultimate Challenge: The 3x + 1 Problem (en anglès). Providence: American Mathematical Society, 2011. ISBN 978-08218-4940-8. 
• Leavens, Gary T.; Vermeulen, Mike «3x + 1 search programs» (en anglès). Computers & Mathematics with Applications, 24(11), desembre 1992. DOI: 10.1016/0898-1221(92)90034-F.
• Letherman, Simon; Schleicher, Dierk; Wood, Reg «The (3n + 1)-problem and holomorphic dynamics» (en anglès). Experimental Mathematics, 8(3), 1999. DOI: 10.1080/10586458.1999.10504402.
• Maddux, Cleborne D.; Johnson, D. Lamont. Logo: A Retrospective (en anglès). Nova York: Haworth Press, 1997. ISBN 0-7890-0374-0.  The problem is also known by several other names, including: Ulam's conjecture, the Hailstone problem, the Syracuse problem, Kakutani's problem, Hasse's algorithm, and the Collatz problem.
• O'Connor, J. J.; Robertson, E. F.. Lothar Collatz (en anglès). Escòcia: St Andrews University School of Mathematics and Statistics, 2006. 
• Ohira, Reiko; Yamashita, Michinori. Una generalització del problema de Collatz (PDF) (en japonès).  Arxivat 2012-03-30 a Wayback Machine.
• Pickover, Clifford A. Wonders of Numbers (en anglès). Oxford: Oxford University Press, 2001. ISBN 0-19-513342-0. 
• Simons, John L. «On the nonexistence of 2-cycles for the 3x + 1 problem» (en anglès). Math. Comp., 74, 2005. Bibcode: 2005MaCom..74.1565S. DOI: 10.1090/s0025-5718-04-01728-4.
• Simons, J.; de Weger, B. «Theoretical and computational bounds for m-cycles of the 3n + 1 problem» (PDF) (en anglès). Acta Arithmetica, 117(1), 2005. Arxivat de l'original el 2017-05-17. Bibcode: 2005AcAri.117...51S. DOI: 10.4064/aa117-1-3 [Consulta: 16 novembre 2022].
• Sinisalo, Matti K. «On the minimal cycle lengths of the Collatz sequences» (en anglès). Universitat d'Oulu, juny 2003. Arxivat de l'original el 2009-10-24. [Consulta: 16 novembre 2022].
• Sinyor, J. «The 3x+1 Problem as a String Rewriting System» (PDF) (en anglès). International Journal of Mathematics and Mathematical Sciences, 2010, 2010, pàg. Article ID 458563, 6 pàgines.
• Stadfeld, Paul. «Blueprint for Failure: How to Construct a Counterexample to the Collatz Conjecture» (en anglès). Arxivat de l'original el 2007-09-26. [Consulta: 16 novembre 2022].
• Steiner, R. P.. «A theorem on the syracuse problem». A: Proceedings of the 7th Manitoba Conference on Numerical Mathematics (en anglès), 1977, p. 553–559. 
• Terras, Riho «A stopping time problem on the positive integers» (PDF) (en anglès). Acta Arithmetica, 30(3), 1976, pàg. 241–252. DOI: 10.4064/aa-30-3-241-252.
• Urata, Toshio. «Some Holomorphic Functions connected with the Collatz Problem» (PDF) (en anglès). Arxivat de l'original el 2004-11-28. [Consulta: 16 novembre 2022].
• Van Bendegem, Jean Paul «The Collatz Conjecture: A Case Study in Mathematical Problem Solving» (PDF) (en anglès). Logic and Logical Philosophy, 14, 2005. Arxivat de l'original el 2022-10-09. DOI: 10.12775/llp.2005.002 [Consulta: 16 novembre 2022].

Vegeu també

• Aritmètica modular
• Dinàmica aritmètica
• Grup afí a classe de residus
• Semigrup 3x + 1

Enllaços externs

• Matthews, Keith. «3 x + 1 page» (en anglès).
• Weisstein, Eric W., «Collatz Problem» a MathWorld (en anglès).
• Collatz Problem a PlanetMath.
• Nochella, Jesse. «Collatz Paths» (en anglès). Wolfram Demonstrations Project.
• «Are computers ready to solve this notoriously unwieldy math problem?» (en anglès). Technology Review.