Usuària:Viquialcon/Àrea del cercle
En geometria, l'àrea tancada per un cercle de radi r és π r2. Aquí la lletra grega Plantilla:Pi r2 representa una constant, aproximadament igual a 3.14159, i que és igual al quocient de la circumferència de qualsevol cercle i elseu diàmetre.
Un mètode de de1⁄2 × 2Plantilla:Pir × rivar aquesta fórmula, el qual va originar amb Archimedes, implica veure el cercle com el límit d'una seqüència de polígons regulars. L'àrea d'un polígon regular és mitja el seu perímetre multiplicat per la distància del seu centre als seus costats, i la fórmula corresponent (allò l'àrea és mitja el perímetre cronometra el radi, i.e. 1⁄2 × 2πr r) controls en el límit per un cercle.
Tot i que sovint referit a com l'àrea d'un cercle en contextos informals, en rigor el disc de terme refereix a l'interior del cercle, mentre el cercle és reservat per la frontera només, el qual és una corba i cobreix cap àrea ell. Per això, l'àrea d'un disc és la frase més precisa per l'àrea tancada per un cercle.
Història[modifica]
Les matemàtiques modernes poden obtenir l'àrea que utilitza els mètodes de càlcul integral o el seu més sofisticat offspring, anàlisi real. Tanmateix l'àrea d'un disc va ser estudiada pels grecs Antics. Eudoxus De Cnidus en el cinquè segle B.C. Va tenir trobat que l'àrea d'un disc és proporcional al seu radi va quadrar. Archimedes va utilitzar les eines de geometria Euclidiana per mostrar que l'àrea dins un cercle és igual a allò d'un triangle correcte la base del qual té la longitud de la circumferència del cercle i l'alçada del qual iguals el radi del cercle en la seva Mida de llibre d'un Cercle. La circumferència és 2πr, i l'àrea d'un triangle és mitja la base cronometra l'alçada, cedint l'àrea π r2 pel disc. Previ a Archimedes, Hippocrates de Chios era el primer per mostrar que l'àrea d'un disc és proporcional a la plaça del seu diàmetre, mentre part de la seva quadratura de la lúnula de Hippocrates, però no va identificar la constant de proportionality.[1][2]
Arguments històrics[modifica]
a vaietat d'arguments ha estat avançada històricament per establir l'equació Un =
r
{\displaystyle Un=\pi r^{2}} de graus variables de rigor matemàtic. El més famós d'aquests és el mètode d'Archimedes de exhaustion, un dels usos més primerencs del concepte matemàtic d'un límit, així com l'origen de l'axioma d'Archimedes que queda part del tractament analític estàndard del sistema de número real. La prova original d'Archimedes és no ben bé rigorós per estàndards moderns, perquè assumeix que podem comparar la longitud de arc d'un cercle a la longitud d'una secant i una línia de tangent, i declaracions similars sobre l'àrea, mentre geomètricament evident.
Utilitzant polígons[modifica]
L'àrea d'un polígon regular és mitja el seu perímetre cronometra l'apotema. Mentre el número de costats dels augments de polígon regulars, el polígon tendeix a un cercle, i l'apotema tendeix al radi. Això suggereix que l'àrea d'un disc és mitja la circumferència del seu bounding el cercle cronometra el radi.[3]
La prova d'Archimedes[modifica]
Archimedes (c. 260 BCE) següent & , comparar l'àrea tancada per un cercle a un triangle correcte la base del qual té la longitud de la circumferència del cercle i l'alçada del qual iguals el radi del cercle . Si l'àrea del cercle no és igual a allò del triangle, llavors hagi de ser qualsevol més gran o menys. Eliminem cadascú d'aquests per contradicció, deixant igualtat com la possibilitat única. Utilitzem polígons regulars de la mateixa manera.
No més gran[modifica]

Suposa que l'àrea C tancat pel cercle és més gran que l'àrea T = 1⁄2cr del triangle. Deixat E denotar la quantitat sobrant. Inscriure una plaça en el cercle, de manera que la seva quatre mentida de cantonades en el cercle. Entre el quadrat i el cercle és quatre segments. Si l'àrea total d'aquells buits, G4, és més gran que E, partit cada arc en mig. Això fa la plaça inscrita a un octàgon inscrit, i produeix vuit segments amb un buit total més petit, G8. Continua partir fins a l'àrea de buit total, Gn, és menys de E. Ara l'àrea del polígon inscrit, Pn = C − Gn, ha de ser més gran que que del triangle.
Però això força una contradicció, de la manera següent. Sorteig una perpendicular del centre al midpoint d'un costat del polígon; la seva longitud, h, és menys del radi de cercle. També, deixat cada costat del polígon té longitud s; llavors la suma dels costats, ns, és menys de la circumferència de cercle. L'àrea de polígon consisteix de n triangles iguals amb alçada h i base s, per això iguals 1⁄2nhs. Però des de h < r i ns < c, l'àrea de polígon ha de ser menys de l'àrea de triangle, 1⁄2cr, una contradicció. Per això, el nostre supòsit que C podria ser més gran que T ha de ser malament.
No menys[modifica]

Suposa que l'àrea tancada pel cercle és menys de l'àrea T del triangle. Deixat D denotar la quantitat de dèficit. Circumscriure una plaça, de manera que el midpoint de cada mentides de vora en el cercle. Si el buit d'àrea total entre el quadrat i el cercle, G4, és més gran que D, tall de les cantonades amb tangents de cercle per fer un octàgon circumscrit, i continuar slicing fins a l'àrea de buit és menys de D. L'àrea del polígon, Pn, ha de ser menys de T.
Això, també, força una contradicció. Per, un perpendicular al midpoint de cada costat de polígon és un radi, de longitud r. I des de la longitud de costat total és més gran que la circumferència, el polígon consisteix de n triangles idèntics amb l'àrea total més gran que T. Un altre cop tenim una contradicció, així que el nostre supòsit que C podria ser menys de T ha de ser malament també.
Per això, hagi de ser el cas que l'àrea tancada pel cercle és precisament el mateix que l'àrea del triangle. Això conclou la prova.
Prova de redisposició[modifica]

Seguint va Seureō Moshun (Smith & Mikami 1914, pp. 130–132) i Leonardo da Vinci (Beckmann 1976, p. 19), podem utilitzar polígons regulars inscrits en una manera diferent. Suposa inscrivim un hexàgon. Tallat l'hexàgon a sis triangles per partir ell del centre. Dos triangles oposats tant tacte dos diàmetres comuns; portaobjectes els al llarg d'un així que les vores radials són adjacents. Ara formen un paral·lelogram, amb els costats d'hexàgon que fan dues vores oposades, un del qual és la base, s. Dues vores radials formen costats esbiaixats, i l'alçada és h (mentre en l'Archimedes prova). De fet, podem reunir tots els triangles a un paral·lelogram gran per posar parells successius després a cadascú altre. El mateix és cert si augmentem a vuit costats etcètera. Per un polígon amb 2n costats, el paral·lelogram tindrà una base de longitud ns, i una alçada h. Mentre el número d'augments de costats, la longitud de la base de paral·lelogram s'apropa mitja la circumferència de cercle, i la seva alçada s'apropa el radi de cercle. En el límit, el paral·lelogram esdevé un rectangle amb amplada πr i alçada r.
Àrea de disc de la unitat per rearranging n polígons. Polígon Paral·lelogram n Costat Base Alçada Àrea 4 1.4142136 2.8284271 0.7071068 2.0000000 6 1.0000000 3.0000000 0.8660254 2.5980762 8 0.7653669 3.0614675 0.9238795 2.8284271 10 0.6180340 3.0901699 0.9510565 2.9389263 12 0.5176381 3.1058285 0.9659258 3.0000000 14 0.4450419 3.1152931 0.9749279 3.0371862 16 0.3901806 3.1214452 0.9807853 3.0614675 96 0.0654382 3.1410320 0.9994646 3.1393502 ∞ 1/∞ π 1 π
Proves modernes[modifica]
Hi ha diverses definicions equivalents de la constant π. La definició convencional en pre-geometria de càlcul és la proporció de la circumferència d'un cercle al seu diàmetre:
Tanmateix, perquè la circumferència d'un cercle no és un concepte analític primitiu, aquesta definició no és adequada en tractaments rigorosos moderns. Una definició moderna estàndard és allò π és igual a dues vegades l'arrel menys positiva del cosine funció o, equivalently, el mig-període del sinus (o cosine) funció. El cosine la funció pot ser definida qualsevol com a sèrie de poder, o mentre la solució d'una equació diferencial segura. Això evita qualsevol referència a cercles en la definició de π, de manera que declaracions sobre la relació de π a la circumferència i l'àrea de cercles és de fet teoremes, més que definicions, que segueixen de les definicions analítiques de conceptes agraden "àrea" i "circumferència".
Les definicions analítiques són vistes per ser equivalent, si és acordat que la circumferència del cercle és mesurada com a rectifiable corba mitjançant la integral
L'integal apareixent a la dreta és un abelian integral el valor el qual és un mig-període de la funió de sinus, igual a π. Per això C = π R = π D {\displaystyle C=2\pi R=\pi D} és vist per ser cert com a teorema.
Molts dels aguments que segueixen ús conceptes únics de càlcul elemental per reproduir la fórmula Un = π r
{\displaystyle =\pi r^{2}} , però dins molts casos per considerar aquests proves tan reals, confien implicitly en el fet que un pot desenvolupar funcions trigonomètriques i la constant fonamental en una manera que és totalment independent de la seva relació a geometria. Hem indicat on pertoqui com cadascú d'aquestes proves pot ser fet totalment independent de tota trigonometria, però dins alguns casos que requereix més sofisticat idees matemàtiques que aquells permès per càlcul elemental.
Prova de ceba[modifica]

Utilitzant càlcul, podem suma l'àrea incrementally, partitioning el disc a anells concèntrics prims com les capes d'una ceba. Això és el mètode d'integració de closca dins dues dimensions. Per un infinitesimally anell prim de la "ceba" de radis t, l'àrea acumulada és 2πt dt, el circumferential la longitud de l'anell cronometra la seva amplada infinitesimal (un pot aproximar aquest anell per un rectangle amb amplada=2πt i alçada=dt). Això dóna una integral elemental per un disc de radis r.
És rigorosament justificat pel multivariate regla de substitució en coordenades polars. És a dir, l'àrea és donada per una integral doble de la funció constant 1 sobre el disc ell. Si D denota el disc, llavors la integral doble pot ser computada en coordenades polars de la manera següent:
Quin és el mateix resultat mentre obtingut damunt.
Una justificació rigorosa equivalent, sense confiar en les coordenades especials de trigonometria, utilitza el coarea fórmula. Definir una funció ρ
2
R {\displaystle \ho :\mathbb {R} ^{}\a \mathbb {R} } per
( x , y ) =
y 2 {\displaystyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}} . La nota ρ és un Lipschitz funció el gradient del qual és un vector d'unitat |
ρ
=
{\displaystyle |\nabla \rho |=1} (gairebé a tot arreu). Deixat D ser el disc
{} en R 2 {\displaystyle \mathbb {R} ^{}} . Mostraem que L 2 ( ) =
{\dispaystyle {\mathcal {L}}^{}(D)=\pi } , on L
{ {\mathcal {L}}^{}} és el bidimensional Lebesgue mesura en R 2 {\displaystyle \mathbb {R} ^{2}} . Assumirem que el-dimensional Hausdorff mesura del cecle
= r {\displaystyle \rho =r} és
r {} , la circumferència del cercle de radis r. (Això pot ser agafat com la definició de circumferència.) Llavors, pel coarea fórmula,
Prova de triangle[modifica]


Similar a la prova de ceba va perfilar damunt, podríem explotar càlcul en una manera diferent per tal d'arribar a la fórmula per l'àrea d'un disc. Considera unwrapping els cercles concèntrics a tires rectes. Això formarà un correcte angled triangle amb r com la seva alçada i 2πr (sent el tall exterior de ceba) com la seva base.
Trobant l'àrea d'aquest triangle donarà l'àrea del disc
Els angles oposats i adjacents per aquest triangle són respectivament en graus 9.0430611..., 80.956939... I en radians 0.1578311... Un233527, 1.4129651... Un233528.Plantilla:OEIS2C![]()
Explícitament, imaginem dividir cap amunt d'un cercle a triangles, cadascú amb un igual d'alçada al radi del cercle i una base que és infinitesimally petit. L'àea e cada d'aqests triangles és iguals a
/
⋅ r d u {\displaystyle 1/2\cdot r\cdot du} . Per summing amunt (integrant) tot de les àrees d'aquests triangles, arribem a la fórmula per l'àrea del cercle :
També pugui ser justificat per una integral doble de la funció constant 1 sobre el disc per invertir l'ordre d'integració i utilitzant un canvi de variables en la integral damunt iterada:
Fent la substitció u = r θ ,
d u =
{\displaystyle u=r\theta ,\ du=r\ d\theta } converteix l'integral a
Quin és el mateix que el damunt resultat.
La prova de triangle pot se reformulated com una aplicació de Verd teorema en flu-forma de dvergència (i.e. una versió bidimensional del teorema de divergència), en una manera que evita tots esmenten de trigonometria i la constant π. Considerar el camp de vector
r = x i
j {\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {} } en l'avió. Així que la divergència de r és igual a dos, i per això l'àrea d'un disc D és igual a
Pe teorema de Green, això és el mateix que el outward flux de r a través del cercle bounding D:
On n és la unitat normal i ds és el arc mesura de longitud. Per un cecle de adis R cetrat a l'origen, hem | r
= R
{ |\mathbf {r} |=R} i n = r / R {\displaystyle \mathbf {n} =\mathbf {r} /R} , així que el damunt la igualtat és
La integal de ds sobre el cercle sencer
D {} és només el arc longitud, el qual és la seva circumferència, així que això mostra que l'àrea Un tancat pel cercle és igual a R /
{\displaystyle R/2} temps la circumferència del cercle.
Semicircle Prova[modifica]
Nota que l'àrea 'un semicicle de adis pot ser computat per la integral
− r r r 2
x
d
{\displaystyle \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx} .
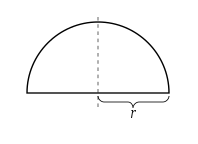
Per substitució trigonomètrica, substituïm x = r θ { =r\pecat \theta } , per això
x = r
d . {\displaystyle dx=r\cos \theta \,d\theta .
El durar el pas segueix des de la identitat trigonomètrica cos ( θ ) = pecat ( π / 2 ) { \(\theta )=\(\pi /-\theta )} implica que cos
{ \cos ^{}\theta } i pecat 2
{ \pecat ^{2}\theta } té integrals iguals sobre l'interval
,
/ 2
{\displaystyle [0,\pi /2]} , utilitzant integració per substitució. Però d'altra banda, des de
2 θ
= 1 { \cos ^{}\theta +\pecat ^{}\theta =} , la suma de les dues integrals és la longitud d'aquell interval, el qual és
/ 2 {\displaystyle \pi /2} . Consegüentment, la integral de
{ \cos ^{2}\theta } és igual a mig la longitud d'aquell interval, el qual és
/ 4 {\displaystyle \pi /} .
Per això, l'àea d'un cercle de radis r, el qual és dues vegades l'àrea del semi-cercle, és igual a 2
π r
=
r
{\displaystyle 2\cdot {\frac {\pi r^{2}}{2}}=\pi r^{2}} .
Aquesta prova particular pot aparèixer per suplicar la qüestió, si el sinus i cosine les funcions van implicar en la substitució trigonomètrica és considerada mentre sent definit amb relació a cercles. Tanmateix, mentre anotat més d'hora, és possible de definir sinus, cosine, i π en una manera que és totalment independent de trigonometria, en quin cas la prova és vàlida pel canvi de fórmula de variables i Fubini teorema, assumint les propietats bàsiques de sinus i cosine (quins també poden ser provats sense assumir qualsevol cosa sobre la seva relació a cercles).
Isoperimetric Desigualtat[modifica]
El cercle és la corba tancada de menys perímetre que tanca l'àrea màxima. Això és sabut com el isoperimetric desigualtat, el qual declara que si un rectifiable Jordan corba en l'avió Euclidià té perímetre C i tanca una àrea Un (pel teorema de corba de la Jordània) llavors
A més,controls d'igualtat en aquesta desigualtat si i només si la corba és un cercle, en aquest
Aproximació ràpida[modifica]
Els càlculs Archimedes van utilitzar per aproximar l'àrea numèricament era laborious, i va parar amb un polígon de 96 costats. Unes idees d'usos de mètode més ràpides de Willebrord Snell (Cyclometricus, 1621), més enllà desenvolupat per Christiaan Huygens (De Circuli Magnitudine Inventa, 1654), va descriure en Gerretsen & Verdenduin (1983, pp. 243–250) & Verdenduin (1983, pp. ).
Archimedes doblant mètode[modifica]
Donat un cercle, deixat un ser el perímetre d'un inscrit regular n-gon, i deixat Un ser el perímetre d'un circumscrit regular n-gon. Llavors un i Un és més baix i superior bounds per la circumferència del cercle que esdevé més agut i més agut com n augments, i la seva mitjana (un + Un)/2 és una aproximació especialment bona a la circumferència. Per computar un i Un per gran n, Archimedes va derivar el següent doblant formulae:
- i
Començant d'un hexàgon, Archimedes va doblar n quatre temps per aconseguir un 96-gon, el qual li va donar una aproximació bona a la circumferència del cercle.
En notació moderna, podem reproduir la seva computació (i anar més llunyà) de la manera següent. Per un cercle d'unitat, un hexàgon inscrit ha u6 = 6, i un hexàgon circumscrit ha U6 = 4√3. Doblant set collites de temps
Archimedes que dobla set temps; n = 6×2k. k n un Un (un + Un)/4 0 6 6.0000000 6.9282032 3.2320508 1 12 6.2116571 6.4307806 3.1606094 2 24 6.2652572 6.3193199 3.1461443 3 48 6.2787004 6.2921724 3.1427182 4 96 6.2820639 6.2854292 3.1418733 5 192 6.2829049 6.2837461 3.1416628 6 384 6.2831152 6.2833255 3.1416102 7 768 6.2831678 6.2832204 3.1415970
(Aquí (un + Un)/2 aproxima la circumferència del cercle d'unitat, el qual és 2π, així que (un + Un)/4 aproxima π.)
El durar l'entrada de la taula té 355⁄113 mentre un de les seves aproximacions racionals millors; i.e., no hi ha cap aproximació millor entre números racionals amb denominador fins a 113. El número 355⁄113 és també una aproximació excel·lent a π, més ben que qualsevol altre número racional amb denominador menys de 16604.[4]
El Snell–Huygens refinament[modifica]
Snell Proposat (i Huygens va provar) un més estanc lligat que Archimedes :
Això per n = 48 dóna una aproximació millor (aproximadament 3.14159292) que el mètode d'Archimedes per n = 768.
Derivation D'Archimedes doblant formulae[modifica]

Deixat un costat d'un inscrit regular n-gon té longitud sn i tocar el cercle a punts Un i B. Deixat Un′ ser el contrari de punt Un en el cercle, de manera que Un′Un és un diàmetre, i Un′AB és un triangle inscrit en un diàmetre. Pel teorema de Thales , això és un triangle correcte amb angle correcte a B. Deixat la longitud d'Un′B ser cn, el qual cridem el complementar de sn; per això cn2+sn2 = (2r)2. Deixat C bisecar el arc de la A a la B, i deixat C′ ser el contrari de punt C en el cercle. Per això la longitud de CA és s2n, la longitud de C′Un és c2n, i C′CA l'és un triangle correcte damunt diàmetre C′C. Perquè C biseca el arc de la A a la B, C′C perpendicularly biseca l'acord de la A a la B, diu a P. Triangle C′AP és per això un triangle correcte, i és similar a C′CA de llavors ençà comparteixen l'angle a C′. Per això tot tres costats corresponents són en la mateixa proporció; en particular, hem C′Un : C′C = C′P : C′Un i AP : C′Un = CA : C′C. El centre del cercle, O, biseca Un′Un, així que també tenim OAP de triangle similar a Un′AB, amb OP mig la longitud d'Un′B. En termes de longituds de costat, això ens dóna
En la primera equació C′P és C′O+OP, longitud r+1⁄2cn, i C′C és el diàmetre, 2r. Per un cercle d'unitat tenim el famós doblant equació de Ludolph furgoneta Ceulen,
Si ara circumscrivim un regular n-gon, amb costat Un″B″ paral·lel a AB, llavors OAB i OA″B″ és triangles similars, amb Un″B″ : OC = d'AB : OP. Trucada el costat circumscrit Sn; llavors això és Sn : sn = 1 : 1⁄2cn. (Un altre cop hem utilitzat que OP és mig la longitud d'Un′B.) Per això obtenim
Anomenem el perímetre inscrit un = nsn, i el circumscrit perimenter Un = nSn. Llavors combinant equacions, tenim
De manera que
Això dóna una equació mitjana geomètrica.
També podem deduir
O
Això dóna una equació mitjana harmònica.
Dart Aproximació[modifica]

Quan mètodes més eficaços de trobar les àrees no són disponibles, podem recórrer a “tirar darts”. Aquest Monte Carlo mètode utilitza el fet que si les mostres aleatòries són agafades uniformement escampat a través de la superfície d'una plaça en quin un disc resideix, la proporció de mostres que copegen el disc aproxima la proporció de l'àrea del disc a l'àrea de la plaça. Això hauria de ser considerat un mètode de durar recurs per computar l'àrea d'un disc (o qualsevol forma), mentre requereix un número enorme de mostres per aconseguir precisió útil; una estimació bona a 10−n requereix aproximadament 100n mostres aleatòries (Thijsse 2006, p. 273).
Redisposició finita[modifica]
Hem vist que per partitioning el disc a un número infinit de peces podem reassemble les peces a un rectangle. Un fet notable va descobrir relativament recentment (Laczkovich 1990) és que podem dissecar el disc a un gran però número finit de peces i llavors reassemble les peces a una plaça d'àrea igual. Això és cridat Tarski problema que quadra cercle. La naturalesa de Laczkovich la prova és tal que prova l'existència de tal partició (de fet, de molts tals particions) però no exhibeix qualsevol partició particular.
Cercles no Euclidians[modifica]
Els cercles poden ser definits dins geometria no Euclidiana, i en particular en l'hiperbòlic i elliptic avions.
Per exemple, l'efera d'unitat S
( ) {\displaystyle S^{2}(1)} és un model pel bidimensional elliptic avió. Porta un intrínsec mètric allò sorgeix per mesurar longitud geodèsica. Els cercles geodèsics són el parallels en un sistema de coordenada geodèsic. M
More precisely, fix a point {\displaystyle \mathbf {z} \in S^{2}(1)} that we place at the zenith. Associated to that zenith is a geodesic polar coordinate system {\displaystyle (\phi ,\theta )}, {\displaystyle 0\leq \phi \leq \pi }, {\displaystyle 0\leq \theta <2\pi }, where z is the point \phi =0. In these coordinates, the geodesic distance from z to any other point {\displaystyle \mathbf {x} \in S^{2}(1)} having coordinates {\displaystyle (\phi ,\theta )} is the value of \phi at x. A spherical circle is the set of points a geodesic distance R from the zenith point z. Equivalently, with a fixed embedding into \mathbb {R} ^{3}, the spherical circle of radius {\displaystyle R\leq \pi } centered at z is the set of x in {\displaystyle S^{2}(1)} such that {\displaystyle \mathbf {x} \cdot \mathbf {z} =\cos R}.
També podem mesurar l'àrea del disc esfèric tancat dins d'un cercle esfèric, utilitzant la mesura d'àrea de superfície intrínseca en l'esfera. L'àrea del disc de radis R és llavors donat per
Mé generalment, si una esfera S
( ρ ) {\displaystyle S^{2}(\rho )} té radi de curvatura
{ } , llavors l'àrea del disc de radis R és donat per
Obseva que, mentre una aplicació de L'Hôpital' regla, això tendeix a l'àrea Euclidiana
R
{\displaystyle \pi R^{2}} en el límit pla
{} .
El cas hiperbòlic és similar, amb l'àrea d'un disc de radi intrínsec R en el (curvatura constant
{} ) l'avió hiperbòlic donat per
On cosh és l'hiperbòlic cosine. Més generalment, per la curvatura constant
{} avió hiperbòlic, la resposta és
Aquestes identitats són importants per desigualtats de comparació dins geometria. Per exemple, l'àrea tancada per un cercle de radis R en un espai pla és sempre més gran que l'àrea d'un cercle esfèric i més petit que un cercle hiperbòlic, va proporcionar tot tres cercles haver-hi igual (intrínsec) radi. Allò és,
Pe
tot R
{} . Intuitively, això és perquè l'esfera tendeix per tòrcer enrere damunt ell, cedint cercles d'àrea més petita que aquells en l'avió, whilst l'avió hiperbòlic, quan immersed a espacial, desenvolupa serrells que produeixen àrea addicional. És més generalment cert que l'àrea del cercle d'un radi fix R és un estrictament funció de decreixement de la curvatura.
Dins tots els casos, si k és la curvatura (constant, positiva o negativa), llavors la desigualtat isoperimètrica per un àmbit amb àrea A i perímetre L ésk
Generalitzacions[modifica]
Podem estendre un disc per formar una el·lipse. Perquè aquest tram és una transformació lineal de l'avió, té un factor de distorsió que canviarà l'àrea però proporcions de conserva d'àrees. Aquesta observació pot soler computar l'àrea d'una el·lipse arbitrària de l'àrea d'un cercle d'unitat.
Considerar el cercle d'unitat circumscrit per una plaça de longitud de costat 2. La transformació envia el cercle a una el·lipse per estendre o encongint els diàmetres horitzontals i verticals a les destrals importants i menors de l'el·lipse. La plaça aconsegueix enviada a un rectangle que circumscriu l'el·lipse. La proporció de l'àrea del cercle a la plaça és π/4, el qual significa la proporció de l'el·lipse al rectangle és també π/4. Suposar un i b és les longituds de les destrals importants i menors de l'el·lipse. Des de l'àrea del rectangle és ab, l'àrea de l'el·lipse és πab/4.
També podem considerar mides anàlegues en dimensions més altes. Per exemple, podem desitjar trobar el volum dins una esfera. Quan tenim una fórmula per l'àrea de superfície, podem utilitzar la mateixa classe de “aproximació” de ceba vam utilitzar pel disc.
Bibliografia[modifica]
- Archimedes (1897), "Measurement of a circle", in Heath, T. L., The Works of Archimedes, Cambridge University Press, <https://archive.org/stream/worksofarchimede029517mbp#page/n279/mode/2up> (1897), "", dins Bruc, T. L., , @Cambridge Premsa Universitària (Al principi publicat per @Cambridge Premsa Universitària, , va basar en J. L. Heiberg versió grega.)
- Beckmann, Petr (Beckmann, Petr (1976), A History of Pi, St. Martin's Griffin, ISBN 978-0-312-38185-1), , ,
- Gerretsen, J.; Verdenduin, P. (1983), "Capítol 8: Polígons i Polyhedra", en H. Behnke; F. Bachmann; K. Fladt; H. Kunle, Fundamentals de Matemàtiques, II de Volum: Geometria, va traduir per S. H. Gould, Gerretsen, J. & Verdenduin, P. (1983), "Chapter 8: Polygons and Polyhedra", in H. Behnke, Fundamentals of Mathematics, Volume II: Geometry, MIT Press, pàg. 243–250, ISBN 978-0-262-52094-2, pp. , (Al principi Grundzüge der Mathematik, Vandenhoeck & Ruprecht, Göttingen, 1971.)
- Laczkovich, Miklós (1990), "Equidecomposability i discrepància: Una solució a Tarski el cercle que quadra problema", Revista für dau reine und angewandte Mathematik, 404: 77–117, SENYOR 1037431[Enllaç no actiu]
- Lange, Serge (1985), "La longitud del cercle", Lange, Serge (1985), "The length of the circle", Math! : Encounters with High School Students, Springer-Verlag, ISBN 978-0-387-96129-3! : Encontres amb Estudiants d'Institut, ,
- Smith, David Eugene; Mikami, Yoshio (1914), Smith, David Eugene & Mikami, Yoshio (1914), A history of Japanese mathematics, Chicago: Open Court Publishing, pàg. 130–132, ISBN 978-0-87548-170-8, <https://archive.org/details/historyofjapanes00smituoft>, Chicago: , pp. ,
- Thijsse, J. M. (2006), Thijsse, J. M. (2006), Computational Physics, Cambridge University Press, pàg. 273, ISBN 978-0-521-57588-1, @Cambridge Premsa Universitària, p. ,
Referències[modifica]
- ↑ [1]. [[Especial:Fonts bibliogràfiques/0-534-39330-6|ISBN 0-534-39330-6]].
- ↑ Heath, Thomas L. (2003), A Manual of Greek Mathematics, Courier Dover Publications, pàg. 121-132, ISBN 0-486-43231-9, <https://books.google.cat/books?id=_HZNr_mGFzQC&pg=PA121>
- ↑ Lliçons dins Geometria: Per l'Ús de Principiants, pàgina 124 (1894).
- ↑ No totes aproximacions racionals millors són el convergents de la fracció continuada
Enllaços externs[modifica]
- Àrea d'una Calculadora de Cercle
- L'àrea tancada per un cercle (amb animació interactiva)
- Notícia de ciència en Tarski problema
- Calcula àrea de disc en fxSolver
[[Categoria:Cercles]]

