Desviació tipus

Representació d'una distribució normal. Cada franja de tonalitat diferent té l'amplada d'una desviació tipus.

Probabilitat acumulada d'una distribució normal amb un valor esperat de 0 i una desviació estàndard d'1.

Un conjunt de dades amb una mitjana de 50 (en blau) i una desviació estàndard (σ) de 20.

Exemple de dues mostres de població amb la mateixa mitjana i diferents desviacions estàndard. La població vermella té una mitjana de 100 i una desviació tipus de 10; la població blava té una mitjana de 100 i una desviació tipus de 50.

La desviació tipus (σ o S), també coneguda com desviació estàndard o desviació típica i abreviada Desv, SD o StDev (de l'anglès Standard Deviation) és una mesura de variabilitat o diversitat que s'usa en estadística i teoria de la probabilitat. Mostra quanta variació o "dispersió" hi ha respecte la mitjana. Una desviació tipus baixa indica que els punts de dades tendeixen a ser propers a la mitjana, mentre que una desviació tipus alta indica que les dades s'estenen al llarg d'un gran rang de valors.

Tècnicament, la desviació estàndard d'una població estadística, conjunt de dades o distribució de probabilitat és l'arrel quadrada de la seva variància. És algebraicament més simple tot i que menys robusta que la desviació mitjana absoluta. Una propietat útil de la desviació tipus és que, a diferència de la variància, està expressada en les mateixes unitats que les de les dades.

A part d'usar-se per expressar la variabilitat d'una població, la desviació estàndard també s'usa per mesurar la confiança en conclusions estadístiques. Per exemple, el marge d'error en una enquesta de dades es determina calculant la desviació estàndard esperada dels resultats si la mateixa enquesta fos duta a terme múltiples vegades. El marge d'error és normalment cap al doble de la desviació estàndard: el radi d'un interval de confiança al 95%. En ciència, els investigadors solen donar la desviació estàndard de les dades experimentals. També és important en finances, en les quals la desviació estàndard de la taxa de retorn d'una inversió econòmica és la mesura de la volatilitat d'aquesta.

Quan la desviació estàndard es refereix a una distribució de probabilitats, una variable aleatòria o una població se l'anomena desviació estàndard poblacional i es representa amb la lletra σ. Quan es refereix a un conjunt de dades (mostra) se l'anomena desviació estàndard mostral o estimador de la desviació estàndard, ja que s'empra com a estimador de la desviació estàndard poblacional, i es representa per la lletra S.

Exemple bàsic

A continuació es mostra el procés per calcular la desviació estàndard d'un conjunt de dades en forma d'exemple. Es considera una població estadística amb els següents valors:

$2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9$

Aquestes vuit dades tenen una mitjana de 5:

$\frac{2 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5$

Per a calcular la desviació estàndard de la població, primer es calcula la diferència de cada dada respecte la mitjana i després s'eleva al quadrat el resultat de cadascun:

$\begin{array}{lll} (2-5)^2 = (-3)^2 = 9 && (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 && (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 && (7-5)^2 = 2^2 = 4 \\ (4-5)^2 = (-1)^2 = 1 && (9-5)^2 = 4^2 = 16 \end{array}$

Per acabar, es calcula la mitjana d'aquests valors i se'n fa l'arrel quadrada:

$\sqrt{ \frac{(9 + 1 + 1 + 1 + 0 + 0 + 4 + 16)}{8} } = 2$

Aquesta quantitat és la desviació estàndard poblacional, i és igual a l'arrel quadrada de la variància. La fórmula és vàlida només si els vuit valors amb els quals s'ha començat conformen la població completa; si, pel contrari, fossin una mostra aleatòria extreta d'una de més gran, llavors s'hauria d'haver usat un valor de 8-1 = 7 al denominador, i la quantitat obtinguda seria la desviació estàndard mostral. Vegeu la secció Estimació per a més detalls.

Definició

Sigui X una variable aleatòria de valor mitjà μ:

$\operatorname{E}[X] = \mu.\,\!$

Aquí l'operador E denota la mitjana o esperança matemàtica de X. La desviació estàndard de X és la quantitat

$\sigma = \sqrt{\operatorname{E}\left[(X - \mu)^2\right]}$

Això és, la desviació estàndard σ (sigma) és l'arrel quadrada de la variància de X o, dit d'una altra manera, és l'arrel quadrada del valor mitjà de (X − μ)².

La desviació estàndard d'una distribució de probabilitat és la mateixa que aquella d'una variable aleatòria que segueix aquesta distribució. No totes les variables aleatòries tenen desviació estàndard, ja que l'esperança no té per què existir sempre. Per exemple, la desviació estàndard d'una variable aleatòria que segueix una distribució de Cauchy no està definida perquè el seu valor esperat μ no està definit.

Variable aleatòria discreta

En el cas que X agafi valors aleatoris d'un conjunt de dades finit x₁, x₂, …, x_N,en el qual cada valor té la mateixa probabilitat, la desviació estàndard és:

$\sigma = \sqrt{\frac{1}{N}\left[(x_1-\mu)^2 + (x_2-\mu)^2 + \cdots + (x_N - \mu)^2\right]}, {\rm \ \ on\ \ } \mu = \frac{1}{N} (x_1 + \cdots + x_N),$

O bé, fent servir la notació de sumatori:

$\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}, {\rm \ \ on\ \ } \mu = \frac{1}{N} \sum_{i=1}^N x_i$

Si en comptes de tenir iguals probabilitats els valors tenen diferents probabilitats (x₁ té probabilitat p₁, x₂ té probabilitat p₂, ..., x_N té probabilitat p_N) la desviació estàndard és:

$\sigma = \sqrt{\sum_{i=1}^N p_i(x_i - \mu)^2}, {\rm \ \ on\ \ } \mu = \sum_{i=1}^N p_i x_i$

Variable aleatòria contínua

La desviació estàndard d'una variable aleatòria contínua X amb una funció de densitat de probabilitat p(x) és:

$\sigma = \sqrt{\int_\mathbf{X} (x-\mu)^2 \, p(x) \, dx}, {\rm \ \ on\ \ } \mu = \int_\mathbf{X} x \, p(x) \, dx$

Les integrals són integrals definides amb la x variant al llarg del conjunt de possibles valors de la variable aleatòria X.

En el cas d'una família paramètrica de distribucions, la desviació estàndard pot ser expressada en termes de paràmetres. Per exemple, en el cas de la distribució log-normal amb paràmetres μ i σ² la desviació estàndard és [(exp(σ²) − 1)exp(2μ + σ²)]^1/2.

Estimació

Es pot trobar la desviació estàndard per una població sencera en casos (com en el test estandarditzat) en els quals cada membre d'una població està mostrat. En casos en els quals això no es pot fer, la desviació estàndard σ s'estima examinant una mostra aleatòria extreta de la població. Alguns estimadors es llistes a continuació.

Amb la desviació estàndard de la mostra

Un estimador per σ que de vegades s'usa és la desviació estàndard de la mostra, denotada per s_N i definida així:

$s_N = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \overline{x})^2}$

On $\scriptstyle\{x_1,\,x_2,\,\ldots,\,x_N\}$ són els valors observats dels elements de la mostra i $\scriptstyle\overline{x}$ és el valor mitjà d'aquestes observacions, mentre que el denominador N és la mida de la mostra.

Aquest estimador té un error quadràtic mitjà uniforme més petit que el de la desviació estàndard mostral i és l'estimador de màxima versemblança quan la població està distribuïda de manera normal; tanmateix, quan s'aplica a una mostra petita o mitjana tendeix a ser massa petit i és un estimador esbiaixat.

La desviació estàndard de la mostra és la mateixa que la desviació estàndard poblacional per una variable aleatòria discreta que assumeix els seus valors precisament del conjunt de dades, en el qual la probabilitat per cada valor és proporcional a la seva multiplicitat dins del propi conjunt.

Amb la desviació estàndard mostral

L'estimador més comú per a σ és una versió ajustada anomenada desviació estàndard mostral, denotat per s i definit així:

$s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - \overline{x})^2}$

On $\scriptstyle\{x_1,\,x_2,\,\ldots,\,x_N\}$ són els valors observats dels objectes de la mostra i $\scriptstyle\overline{x}$ és el valor mitjà d'aquestes observacions. Aquesta correcció (l'ús de N − 1 en comptes de N) es coneix com correcció de Bessel; la raó per aquesta correcció és que s² és un estimador sense biaix per la variància σ² de la població, si aquesta variància existeix i els valors mostrals són extrets independentment i amb substitució. De totes maneres, s no és un estimador sense biaix per la desviació estàndard σ; tendeix a sobreestimar la desviació estàndard poblacional.

El terme desviació estàndard de la mostra s'usa per l'estimador sense corregir (que usa N al denominador) mentre que el terme desviació estàndard mostral s'usa per l'estimador corregit (que usa N − 1). El denominador N − 1 és el nombre de graus de llibertat al vector de residuals, $\scriptstyle(x_1-\overline{x},\; \dots,\; x_n-\overline{x})$.

Altres estimadors

Vegeu també: Estimació sense biaix de la desviació estàndard i Biaix estadístic

Tot i que es coneix un estimador sense biaix per a σ quan la variable aleatòria és normal, la fórmula és complicada i necessita correccions menors.

Identitats i propietats matemàtiques

La desviació estàndard és invariant sota canvis en localització, i s'escala directament amb l'escala de la variable aleatòria. Per tant, per una constant c i dues variables aleatòries X i Y:

$\operatorname{Desv}(X + c) = \operatorname{Desv}(X), \,$

$\operatorname{Desv}(cX) = \|c\| \operatorname{Desv}(X). \,$

La desviació estàndard de la suma de dues variables aleatòries es pot relacionar amb les seves desviacions estàndard individuals i la covariància entre elles:

$\operatorname{Desv}(X + Y) = \sqrt{\operatorname{Var}(X) + \operatorname{Var}(Y) + 2 \,\operatorname{Cov}(X,Y)}. \,$

On $\scriptstyle\operatorname{Var} \,=\, \operatorname{Desv}^2$ i $\scriptstyle\operatorname{Cov}$ signifiquen variància i covariància respectivament.

El càlcul de la suma de desviacions al quadrat es pot relacionar als moments calculats directament de les dades. La desviació estàndard de la mostra es pot computar com:

$\operatorname{Desv}(X) = \sqrt{E[X-E(X)]^2} = \sqrt{E[X^2] - (E[X])^2}.$

La desviació estàndard mostral es pot calcular com:

$\operatorname{Desv}(X) = \sqrt{\frac{N}{N-1}} \sqrt{E[X-E(X)]^2}.$

Per una població finita amb igual probabilitat a tots els punts, es té:

$\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\overline{x})^2} = \sqrt{\frac{1}{N} \left(\sum_{i=1}^N x_i^2\right) - \overline{x}^2}.$

Per tant, la desviació estàndard és igual a l'arrel quadrada de la mitjana dels quadrats menys el quadrat de la mitjana.

Interpretació i aplicació

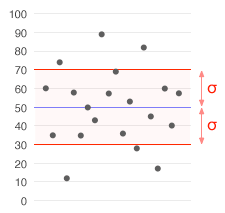
La desviació estàndard és una mesura del grau de dispersió de les dades respecte al valor mitjà; dit d'una altra manera, la desviació estàndard és simplement el "promig" o variació esperada respecte a la mitjana aritmètica.

Per exemple, les tres mostres {0, 0, 14, 14}, {0, 6, 8, 14} i {6, 6, 8, 8} tenen cada una una mitjana de 7. Les seves desviacions estàndard són 7, 5 i 1 respectivament. La tercera població té una desviació estàndard molt més petita que les altres dues perquè tots els seus valors són propers a 7. Dit de manera planera, la desviació estàndard diu com de lluny tendeixen a estar els punts dades de la mitjana. Tindrà, a més, les mateixes unitats que els punts de dades mateixos. Si, per exemple, el conjunt de dades {0, 6, 8, 14} representa les edats d'una població de quatre familiars en anys, la desviació mitjana és de 5 anys. Com un altre exemple, la població {1000, 1006, 1008, 1014} pot representar la distància recorreguda per quatre atletes mesurada en metres; llavors, la mitjana de distància recorreguda és de 1007 metres, i la desviació estàndard és de 5 metres.

La desviació estàndard es pot interpretar com una mesura d'incertesa. La desviació estàndard d'un grup repetit de mesures dóna la precisió d'aquestes. Quan es vol determinar si un grup de mesures està d'acord amb un model teòric, la desviació estàndard d'aquestes mesures és de vital importància: si la mitjana de les mesures està massa allunyada de la predicció (amb la distància mesurada en desviacions estàndard), llavors es considera que les mesures experimentals contradiuen la teoria, la qual cosa és coherent ja que les mesures cauen fora del rang de valors en el qual seria raonable esperar que estiguessin si el model teòric fos correcte.

La desviació estàndard és un dels tres paràmetres de tendència central: mostra l'agrupació de les dades al voltant d'un valor central (la mitjana).

Desigualtat de Txebixev

Una observació no sol estar més lluny que unes poques desviacions estàndard de la mitjana. La desigualtat de Txebixev assegura que, per totes les distribucions per les quals està definida la desviació estàndard, la quantitat de dades dins un nombre de desviacions estàndard de la mitjana és com a mínima tant com està establert en la taula següent:

Població mínima	Distància de la mitjana
50%	√2
75%	2
89%	3
94%	4
96%	5
97%	6
$\scriptstyle 1-\frac{1}{k^2}$	$\scriptstyle k$

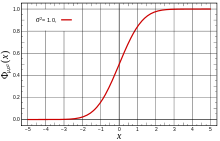
Regles per dades distribuïdes normalment

El blau fosc està a menys d'una desviació estàndard de la mitjana. Per la distribució normal, això és el 68,27 per cent del conjunt; dues desviacions estàndard de la mitjana (blau fosc i blau) són el 95,45 per cent; tres desviacions (blau fosc, blau i blau clar) són el 99,73 per cent; i quatre desviacions són el 99,994 per cent. Els dos punts de la corba que estan a una desviació estàndard de la mitjana són també els punts d'inflexió.

El teorema del límit central postula que la distribució d'una mitjana de moltes variables aleatòries independents i idènticament distribuïdes tendeix cap a la famosa distribució en forma de campana (distribució normal) amb una funció de densitat de probabilitat de:

$\frac{1}{\sigma\sqrt{2\pi}} \exp\!\left(-\frac{[x-\mu]^2}{2\sigma^2} \right)$

On μ és l'esperança matemàtica de les variables aleatòries i σ equival a la desviació estàndard de la seva distribució divida per n^1/2 i n és el nombre de variables aleatòries. La desviació estàndard és doncs només una variable d'escala que ajusta com d'ampla serà la corba, tot i que apareix en la constant normalitzant.

Si una distribució de dades és aproximadament normal llavors la proporció de dades dins de z desviacions estàndard de la mitjana és definida per:

Proporció = $\operatorname{ferr}\left(\frac{z}{\sqrt{2}}\right)$

On $\scriptstyle\operatorname{ferr}$ és la funció error. Si la distribució de dades és aproximadament normal llavors prop del 68% dels valors de les dades estan dins d'una desviació estàndard de la mitjana (matemàticament, μ ± σ, on μ és la mitjana aritmètica), prop del 95% estan dins dues desviacions estàndard (μ ± 2σ) i prop del 99.7% cauen dins tres desviacions estàndard (μ ± 3σ). Això es coneix com la regla 68-95-99,7.

Per diversos valors de z, el percentatge de valors esperats en caure dins i fora l'interval simètric CI = (−zσ, zσ) són els següents:

zσ	Percentatge dins el CI	Percentatge fora el CI	Fracció fora el CI
0,674σ	50%	50%	1 / 2
1σ	68,2689492%	31,7310508%	1 / 3,1514872
1,645σ	90%	10%	1 / 10
1,960σ	95%	5%	1 / 20
2σ	95,4499736%	4,5500264%	1 / 21,977895
2,576σ	99%	1%	1 / 100
3σ	99,7300204%	0,2699796%	1 / 370,398
3,2906σ	99,9%	0,1%	1 / 1000
4σ	99,993666%	0,006334%	1 / 15.787
5σ	99,9999426697%	0,0000573303%	1 / 1744278
6σ	99,9999998027%	0,0000001973%	1 / 506.800.000
7σ	99,999 999 999 7440%	0,0000000002560%	1 / 390700000000

Relació entre la desviació estàndard i la mitjana

La mitjana i la desviació estàndard d'un conjunt de dades normalment es donen conjuntament. En cert sentit, la desviació estàndard és la mesura "natural" de la dispersió estadística si el centre de les dades es mesura sobre la mitjana; això passa perquè la desviació estàndard des de la mitjana és menor que des de qualsevol altre punt. L'enunciat precís és el següent: es suposa que x₁, ..., x_n són nombres reals i es defineix la funció:

$\sigma(r) = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - r)^2}$

Usant càlcul o completant el quadrat és possible demostrar que σ(r) té un mínim únic a la mitjana:

$r = \overline{x}\,$

La variabilitat també pot ser mesurada pel coeficient de variació, que és la proporció de la desviació estàndard respecte la mitjana. És un nombre adimensional.

Sovint es vol alguna informació sobre la precisió de la mitjana obtinguda. La desviació estàndard de la mitjana està relacionada amb la desviació estàndard de la distribució per:

$\sigma_{\text{mitjana}} = \frac{1}{\sqrt{N}}\sigma$

On N és el nombre d'observacions a la mostra usada per estimar la mitjana. Això es pot provar fàcilment amb:

$\begin{align} \operatorname{Var}(X) &\equiv \sigma^2_X\\ \operatorname{Var}(X_1+X_2) &\equiv \operatorname{Var}(X_1) + \operatorname{Var}(X_2)\\ \operatorname{Var}(cX_1) &\equiv c^2 \, \operatorname{Var}(X_1) \end{align}$

Per la qual cosa:

$\begin{align} \operatorname{Var}(\text{mitjana}) &= \operatorname{Var}\left (\frac{1}{N} \sum_{i=1}^N X_i \right) = \frac{1}{N^2}\operatorname{Var}\left (\sum_{i=1}^N X_i \right ) \\ &= \frac{1}{N^2}\sum_{i=1}^N \operatorname{Var}(X_i) = \frac{N}{N^2} \operatorname{Var}(X) = \frac{1}{N} \operatorname{Var} (X). \end{align}$

I com a resultat:

$\sigma_\text{mitjana} = \frac{\sigma}{\sqrt{N}}$

Mètodes ràpids de càlcul

Vegeu també: Algorismes per calcular la variància

Les dues següents fórmules poden representar una desviació estàndard contínua. Un conjunt de tres sumes de potències s₀, s₁, s₂ són cadascuna computada sobre un conjunt de N valors de x, denotat com x₁, ..., x_N:

$\ s_j=\sum_{k=1}^N{x_k^j}$

Cal notar que s₀ eleva x a la potència zero, i com que x⁰ és sempre 1, s₀ s'evalua a N.

Donats els valors d'aquests tres sumatoris, els valors s₀, s₁, s₂ poden ser usats en qualsevol moment per calcular la desviació estàndard actual:

$\sigma = \frac{1}{s_0}\sqrt{s_0s_2-s_1^2}$

De manera similar, per la desviació estàndard mostral:

$s = \sqrt{\frac{s_0s_2-s_1^2}{s_0(s_0-1)}}$

En implementació en ordinadors, quan les tres sumes s_j esdevenen molt gran es necessita considerar l'error d'arrodoniment i el desbordament aritmètic. El mètode a continuació calcula el mètode de les sumes amb errors d'arrodoniment reduïts:

$\begin{align} A_0 &= 0\\ A_i &= A_{i-1}+\frac{1}{i}(x_i-A_{i-1}) \end{align}$

On A és el valor mitjà.

$\begin{align} Q_0 &= 0\\ Q_i &= Q_{i-1}+\frac{i-1}{i} (x_i-A_{i-1})^2 = Q_{i-1}+ (x_i-A_{i-1})(x_i-A_i) \end{align}$

Variància mostral:

$s^2_n=\frac{1}{n-1}Q_n$

Variància estàndard:

$\sigma^2_n=\frac{1}{n}Q_n$

Càlcul ponderat

Quan els valors x_i estan ponderats amb pesos desigual w_i, les sumesde potències s₀, s₁, s₂ són computades cadascuna com:

$\ s_j=\sum_{k=1}^N{w_k x_k^j}\,$

I les equacions de desviació estàndard romanen sense canviar. Cal notar que s₀ és ara la suma dels pesos i no el nombre de mostres N.

El mètode incremental amb errors d'arrodoniment reduïts també pot ser aplicat, però amb alguna complexitat addicional. S'ha de computar una suma de pesos:

$\begin{align} W_0 &= 0\\ W_i &= W_{i-1} + w_i \end{align}$

I els llocsm on s'usa 1/i a sobre han de ser reemplaçats per w_i/W_i:

$\begin{align} A_0 &= 0\\ A_i &= A_{i-1}+\frac{w_i}{W_i}(x_i-A_{i-1})\\ Q_0 &= 0\\ Q_i &= Q _{i-1} + \frac{w_i W_{i-1}}{W_i}(x_i-A_{i-1})^2 = Q_{i-1}+w_i(x_i-A_{i-1})(x_i-A_i) \end{align}$

En la divisió final:

$\sigma^2_n=\frac{Q_n}{W_n}\,$

I:

$s^2_n = \frac{n'}{n'-1}\sigma^2_n\,$

On n és el nombre total d'elements i n' és el nombre d'elements amb pesos diferents de zero.

Les fórmules de sobre esdevenen iguals que les fórmules simplificades de seccions anteriors si els pesos s'assumeixen tots iguals a la unitat.

Combinació de desviacions estàndard

Estadístiques basades en la població

Les poblacions de conjunts, que es poden sobreposar, es poden calcular de manera simple de la manera següent:

$\begin{align} &&N_{X \cup Y} &= N_X + N_Y - N_{X \cap Y}\\ X \cap Y = \varnothing &\Rightarrow &N_{X \cap Y} &= 0\\ &\Rightarrow &N_{X \cup Y} &= N_X + N_Y \end{align}$

Les desviacions estàndard de sub-poblacions que no es sobreposen (X ∩ Y = ∅) poden ser agregades de la següent manera si la mida (actual o relativa a un altre) i les mitjanes de cadascuna són conegudes:

$\begin{align} \mu_{X \cup Y} &= \frac{ N_X \mu_X + N_Y \mu_Y }{N_X + N_Y} \\ \sigma_{X\cup Y} &= \sqrt{ \frac{N_X \sigma_X^2 + N_Y \sigma_Y^2}{N_X + N_Y} + \frac{N_X N_Y}{(N_X+N_Y)^2}(\mu_X - \mu_Y)^2 } \end{align}$

Per un cas més general de M poblacions que no es sobreposen, X₁ fins a X_M, i la població agregada $\scriptstyle X \,=\, \bigcup_i X_i$:

$\begin{align} \mu_X &= \frac{ \sum_i N_{X_i}\mu_{X_i} }{ \sum_i N_{X_i} } \\ \sigma_X &= \sqrt{ \frac{ \sum_i N_{X_i}(\sigma_{X_i}^2 + \mu_{X_i}^2) }{ \sum_i N_{X_i} } - \mu_X^2 } = \sqrt{ \frac{ \sum_i N_{X_i}\sigma_{X_i}^2 }{ \sum_i N_{X_i} } + \frac{ \sum_{i<j} N_{X_i}N_{X_j} (\mu_{X_i}-\mu_{X_j})^2 }{\big(\sum_i N_{X_i}\big)^2} } \end{align}$

On:

$X_i \cap X_j = \varnothing, \quad \forall\ i<j.$

Si la mida (actual o relativa a un altre), la mitjana i la desviació estàndard de les dues poblacions que es sobreposen són conegudes per les poblacions i també per la seva intersecció, llavors la desviació estàndard de la població general pot ser calculada de la següent manera:

$\begin{align} \mu_{X \cup Y} &= \frac{1}{N_{X \cup Y}}\left(N_X\mu_X + N_Y\mu_Y - N_{X \cap Y}\mu_{X \cap Y}\right)\\ \sigma_{X \cup Y} &= \sqrt{\frac{1}{N_{X \cup Y}}\left(N_X[\sigma_X^2 + \mu _X^2] + N_Y[\sigma_Y^2 + \mu _Y^2] - N_{X \cap Y}[\sigma_{X \cap Y}^2 + \mu _{X \cap Y}^2]\right) - \mu_{X\cup Y}^2} \end{align}$

Si dos o més conjunts de dades són afegits punt per punt, la desviació estàndard del resultat pot ser calculada si es coneix la desviació estàndard de cada conjunt de dades i la covariància de cada parell de conjunts de dades:

$\sigma_X = \sqrt{\sum_i{\sigma_{X_i}^2} + \sum_{i,j}\operatorname{Cov}(X_i,X_j)}$

Pel cas especial en el qual no existeix correlació entre cap parell de conjunts de dades, la relació es redueix al valor eficaç:

$\begin{align} &\operatorname{Cov}(X_i, X_j) = 0,\quad \forall i<j\\ \Rightarrow &\;\sigma_X = \sqrt{\sum_i {\sigma_{X_i}^2}} \end{align}$

Estadístiques basades en la mostra

Les desviacions estàndard de sub-mostres que no es sobreposen (X ∩ Y = ∅) poden ser agregades com segueix si es coneixen les seves mides i mitjanes:

$\begin{align} \mu_{X \cup Y} &= \frac{1}{N_{X \cup Y}}\left(N_X\mu_X + N_Y\mu_Y\right)\\ \sigma_{X \cup Y} &= \sqrt{\frac{1}{N_{X \cup Y} - 1}\left([N_X - 1]\sigma_X^2 + N_X\mu_X^2 + [N_Y - 1]\sigma_Y^2 + N_Y\mu _Y^2 - [N_X + N_Y]\mu_{X \cup Y}^2\right) } \end{align}$

Pel cas més general de M conjunts de dades que no es sobreposen, X₁ fins a X_M, i el conjunt de dades agregades $\scriptstyle X \,=\, \bigcup_i X_i$:

$\begin{align} \mu_X &= \frac{1}{\sum_i { N_{X_i}}} \left(\sum_i { N_{X_i} \mu_{X_i}}\right)\\ \sigma_X &= \sqrt{\frac{1}{\sum_i {N_{X_i} - 1}} \left( \sum_i { \left[(N_{X_i} - 1) \sigma_{X_i}^2 + N_{X_i} \mu_{X_i}^2\right] } - \left[\sum_i {N_{X_i}}\right]\mu_X^2 \right) } \end{align}$

On:

$X_i \cap X_j = \varnothing,\quad \forall i<j$

Si es coneixen la mida, mitjana i desviació estàndard de dos mostres que se sobreposen per les mostres i també per la seva intersecció, llavors la desviació estàndard de la mostra agregada encara pot ser calculada. En general:

$\begin{align} \mu_{X \cup Y} &= \frac{1}{N_{X \cup Y}}\left(N_X\mu_X + N_Y\mu_Y - N_{X\cap Y}\mu_{X\cap Y}\right)\\ \sigma_{X \cup Y} &= \scriptstyle{ \sqrt{ \frac{1}{N_{X \cup Y} - 1}\left([N_X - 1]\sigma_X^2 + N_X\mu_X^2 + [N_Y - 1]\sigma_Y^2 + N_Y\mu _Y^2 - [N_{X \cap Y}-1]\sigma_{X \cap Y}^2 - N_{X \cap Y}\mu_{X \cap Y}^2 - [N_X + N_Y - N_{X \cap Y}]\mu_{X \cup Y}^2\right) } } \end{align}$

Història

El terme desviació estàndard va ser usat per primera vegada per Karl Pearson l'any 1894; aquest l'usava sovint en les seves conferències. Fou un reemplaçament per noms alternatius més antics per la mateixa idea: per exemple, Gauss usava error mitjà.

Bibliografia

• Weisstein, Eric W. Chapman&Hall. CRC Concise Encyclopedia of Mathematics (en anglès), 1999. ISBN 0-8493-9640-9. 

Vegeu també

• Desigualtat de Samuelson
• Desigualtat de Txebixev
• Desviació (estadística)
• Desviació estàndard geomètrica
• Distància de Mahalanobis
• Error absolut mitjà
• Error estàntard
• Mètode de Yamartino
• Mida de la mostra
• Precisió i exactitud
• Valor eficaç
• Volatilitat (finances)

Enllaços externs

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Desviació tipus

• «Glossari d'estadística». Edu365.cat.
• «A simple way to understand Standard Deviation» (en anglès).
• «Online Standard Deviation Calculator» (en anglès).
• «A Guide to Understanding & Calculating Standard Deviation» (en anglès).
• «C++ Source Code» (en anglès). (llicència lliure). Implementació en C++ del càlcul de la mitjana, variància i desviació estàndard.
• «Interactive Demonstration and Standard Deviation Calculator» (en anglès).
• «Standard Deviation – an explanation without maths» (en anglès).
• «Standard Deviation, an elementary introduction» (en anglès).
• «Standard Deviation, a simpler explanation for writers and journalists» (en anglès).
• «Standard Deviation Calculator» (en anglès).
• «Texas A&M Standard Deviation and Confidence Interval Calculators» (en anglès).
• «The concept of Standard Deviation is shown in this 8 m. tall Probability Machine (named Sir Francis) comparing stock market returns to the randomness of the beans dropping through the quincunx pattern. de Index Funds Advisors IFA.com]» (en anglès).