Vòrtex de Görtler

Els vòrtexs de Görtler són vòrtexs longitudinals contrarotatius en parelles que apareixen en una capa límit que es desenvolupa sobre una paret còncava. Van ser explicats per Henry Görtler com a resultat de la inestabilitat relacionada amb l'acceleració centrífuga.

Aquests vòrtexs interactuen amb les ones de Tollmian-Schlichting (ones TS) i donen lloc a una transició laminar-turbulent més ràpida que la relacionada amb la inestabilitat natural prevista per l'equació d'Orr-Sommerfeld.

S'ha trobat experimentalment que la seva aparença depèn en gran manera de la turbulència aigües amunt.

Nombre de Görtler

Esquema de la inestabilitat de Görtle

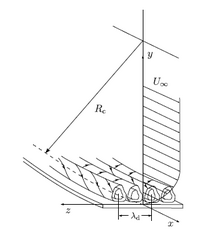
Comencem per les equacions de Navier-Stokes per a un flux incompressible de capa límit d'una placa plana, definida per les equacions de Blasius en un sistema relacionat amb la paret curvilínia (vegeu la imatge) i definida per les variables ($x$, $y$, $z$). Definim una dimensió característica $L$ per

$L={\sqrt {\frac {\nu x}{U_{\infty }}}}$

Aquesta longitud és el gruix de desplaçament de la capa límit a un coeficient proper.

El nombre de Reynolds val

$Re={\frac {U_{\infty }L}{\nu }}$

on

• $U_{\infty }$ = velocitat fora de la capa límit,
• $\nu$ = viscositat cinemàtica,
• $x$ = distància a l'origen de la capa límit.

El radi de curvatura adimensional ${\frac {R_{c}}{L}}$ se suposa que és petit davant de la unitat.

Definim el nombre de Görtler com:

$G=Re\left({\frac {L}{R_{c}}}\right)^{1/2}$

Per tant, aquest nombre mesura els efectes de la curvatura respecte als efectes viscosos.

Pertorbació de la solució estacionària

Com en qualsevol problema d'estabilitat, superposem sobre la solució bàsica una pertorbació on s'estudia la seva evolució espaciotemporal:

• la velocitat reduïda per $U_{\infty }$ té per components $\mathbf {u} (\xi ,y)=[u(\xi ,y),v(\xi ,y),0]$: on li superposem una pertorbació $\mathbf {u} '(\xi ,y,z)=(u',v',w')$ tal que $||\mathbf {u} '||<<||\mathbf {u} ||$,
• de la mateixa manera, la pressió reduïda per $\rho U_{\infty }^{2}$ està pertorbada pel terme $p'$ tal que $p'<<p$.

En conservar només els termes del primer ordre, es pot escriure el sistema:

${\frac {\partial u'}{\partial \xi }}+{\frac {\partial v'}{\partial y}}+{\frac {\partial w'}{\partial z}}=0$

$u{\frac {\partial u'}{\partial \xi }}+u'{\frac {\partial u}{\partial \xi }}+v{\frac {\partial u'}{\partial y}}+v'{\frac {\partial u}{\partial y}}-{\frac {\partial ^{2}u'}{\partial y^{2}}}-{\frac {\partial ^{2}u'}{\partial z^{2}}}=0$

$u{\frac {\partial v'}{\partial \xi }}+u'{\frac {\partial v}{\partial \xi }}+v'{\frac {\partial v}{\partial y}}+v{\frac {\partial v'}{\partial y}}+2G^{2}uu'+{\frac {\partial p'}{\partial y}}-{\frac {\partial ^{2}v'}{\partial y^{2}}}-{\frac {\partial ^{2}v'}{\partial z^{2}}}=0$

$u{\frac {\partial w'}{\partial \xi }}+v{\frac {\partial w'}{\partial y}}+{\frac {\partial p'}{\partial z}}-{\frac {\partial ^{2}w'}{\partial y^{2}}}-{\frac {\partial ^{2}w'}{\partial z^{2}}}=0$

amb les condicions de contorn

$u'=v'=w'=0$ per a $y=0$ i $y\to \infty$

L'escriptura mostra el nombre de Görtler a conseqüència de l'adimensionament. S'ha de tenir en compte que, en les equacions de conservació del moment, l'evolució dels components en $y$ i $z$ s'uneix a la fluctuació de pressió, però no en $x$, que és coherent amb l'estructura de vòrtex.

Aquest sistema d'equacions és de caràcter parabòlic i, per tant, es pot resoldre mitjançant un pas a l'espai (càlcul avançant pla a pla).

Resultats

S'utilitzen dos mètodes per resoldre el problema:

• en el primer estudiem l'estabilitat del sistema utilitzant una pertorbació independent de $x$:

$u'=u''(y)\cos(\alpha z)e^{\beta x}$

$v'=v''(y)\cos(\alpha z)e^{\beta x}$

$w'=w''(y)\sin(\alpha z)e^{\beta x}$

$p'=p''(y)\cos(\alpha z)e^{\beta x}$

on el nombre d'ona de la pertorbació $\alpha$ (un paràmetre del problema) està definit per

$\alpha ={\frac {2\pi L}{\lambda _{d}}}$

$\beta$ és la solució del problema: $\beta >0$ correspon a una solució creixent en $x$, per tant a una situació d'inestabilitat.

El mètode consisteix llavors a estudiar les solucions del problema dels valors propis en l'equació d'Orr-Sommerfeld.

• la segona és una simulació directa per un desplaçament a l'espai des d'una pertorbació inicial raonablement seleccionada.

Aquests dos mètodes donen resultats similars: la inestabilitat de Görtler apareix per G> 0,3 i per longituds d'ona llargues. Les mesures de túnel de vent donen valors significativament més alts i depenen significativament de les pertorbacions.