Força de Lorentz
| Electromagnetisme |
|---|
 |
| Electricitat · Magnetisme |

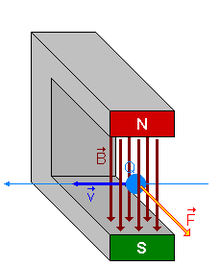
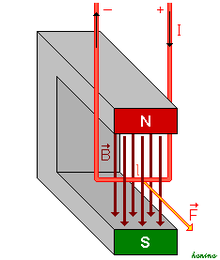
En física, la força de Lorentz és la força exercida sobre una partícula carregada que es mou en un camp electromagnètic. Rep el seu nom en honor del físic holandès Hendrik Lorentz.
Els historiadors suggereixen que la llei està implícita en un article de James Clerk Maxwell, publicat l'any 1865.[1] Hendrik Lorentz va arribat a una derivació completa l'any 1895,[2] identificar la contribució de la força elèctrica uns anys després que Oliver Heaviside identifiqués correctament la contribució de la força magnètica.[3]
Definició[modifica]
Donada una càrrega elèctrica puntual en moviment amb velocitat per una regió caracteritzada per la presència d'un camp magnètic , la partícula carregada experimentarà una força qE deguda al camp elèctric i una força qv × B deguda al camp magnètic segons la següent equació:
on:
- F és la força (en newtons)
- E és el camp elèctric (en volts per metre)
- B és el camp magnètic (en webers per metre quadrat, o en tesles)
- q és la càrrega elèctrica de la partícula (en coulombs)
- v és la velocitat instantània de la partícula (en metres per segon)
- i és el producte vectorial.
En conseqüència, una partícula carregada positivament serà accelerada en la mateixa orientació lineal que el camp E, però es corbarà perpendicularment al camp B d'acord amb la regla de la mà dreta.
Variacions d'aquest fórmula descriuen la força magnètica en un cable amb corrent (sovint anomenat força de Laplace), la força electromotriu d'una espira que es mou a través d'un camp magnètic (un aspecte de la llei de la inducció magnètica de Faraday), i la força en una partícula carregada en moviment.[4]
Força exercida per un conductor per on hi passa corrent[modifica]
Quan un cable elèctric que porta un corrent elèctric es col·loca en un camp magnètic, cada una de les càrregues que s'estan movent —i que formen el corrent elèctric— experimenten la força de Lorentz, i junts poden crear una força macroscòpica en el cable (sovint anomenada força de Laplace). Combinant l'anterior llei de la força de Lorentz i la definició del corrent elèctric, en el cas d'un cable recte, estacionari:
on ℓ és el vector que indica la longitud del cable, i que la seva direcció és al llarg del cable, alineada amb la direcció convencional del flux de la I.
Si el cable no és recte però és corbat, la força que exerceix pot ser calculada utilitzant l'anterior formula a cada segment infinitesimal del cable dℓ, i després sumant totes aquestes forces per integració. La força neta en un cable rígid, estacionari, que transporta un corrent constant I és
La Força de Lorentz a la Relativitat Especial[modifica]
Quan la velocitat d'una partícula s'aproxima a la velocitat de la llum, l'equació de la força de Lorentz s'ha de modificar d'acord amb la relativitat especial:
on
s'anomena factor de Lorentz i és la velocitat de la llum al buit.
Aquesta expressió difereix de l'obtinguda de la força de Lorentz com un factor de .
El canvi d'energia degut als camps és
Forma covariant de la força de Lorentz[modifica]
L'equació de la força de Lorentz es pot escriure en forma covariant, en termes de tensor d'intensitat de camp.
- on
- és c vegades el temps propi de la partícula,
- q és la càrrega elèctrica,
- u és la quadrivelocitat de la partícula, definida com:
- i
- F és el tensor d'intensitat de camp o tensor electromagnètic i en termes dels camps s'escriu com:
- .
Els camps es transformen en un quadre que es mou a velocitat relativa constant segons:
on és la transformació de Lorentz.
Derivació[modifica]
El component de la força és
Aquí, és el temps propi de la partícula. Substituint els components del tensor electromagnètic F dona
Escrivint la quadrivelocitat en termes de velocitat ordinària dona
El càlcul de o és similar donant
- ,
que és la llei de la força de Lorentz.
Història[modifica]

Els primers intents de descriure quantitativament la força electromagnètica va ser duts a terme a mitjans del segle xviii. Es va proposar que la força en pols magnètics, per Johann Tobias Mayer i altres l'any 1760,[5] i d'objectes carregats elèctricament, per Henry Cavendish l'any 1762,[6] obeïa una llei de l'invers del quadrat. Tanmateix, en tots dos casos l'experiència no era ni completa ni concloent. No va ser fins a l'any 1784 que Charles-Augustin de Coulomb, utilitzant una balança de torsió, va poder mostrar definitivament que això era veritat de forma experimental.[7] Poc després del descobriment l'any 1820 per part de Hans Christian Ørsted que una agulla magnètica rep l'acció d'una corrent voltaica, André-Marie Ampère aquell mateix any va poder idear a partir de l'experimentació la fórmula de la dependència angular de la for+an entre dos elements amb corrent.[8][9] En totes aquestes descripcions, la força era sempre descrita en termes de les propietats de la matèria implicades i les distàncies entre dues masses o càrregues, i no en termes dels camps elèctrics i magnètics.[10]
El concepte modern de camp elèctric i magnètic va aparèixer per primer cop en les teories de Michael Faraday, particularment en la seva idea de línies de força, i va rebre una descripció matemàtica més completa posteriorment de la mà de Lord Kelvin i James Clerk Maxwell.[11] Des d'una perspectiva moderna es pot identificar en la formulació de Maxwell de 1865 de les seves equacions de camp una forma de l'equació de la força de Lorentz en relació a la corrent elèctrica,[1] tot i que en l'època de Maxwell no estava clar com les podien estar relacionades les seves equacions amb les forces dels objectes carregats en moviment. J. J. Thomson va ser el primer que va intentar derivar les forces electromagnètiques en objectes carregats en moviment en termes de les propietats de l'objecta i dels camps externs sa partir de les equacions de camp de Maxwell. Interessat en determinar el comportament electromagnètic de les partícules carregades en els raigs catòdics, Thomson va publicar un article l'any 1881 en què donava la força en una partícula deguda a un camp magnètic extern com[3][12]
Aplicacions[modifica]
La força de Lorentz és un principi que s'aprofita en molts dispositius com ara:
- Ciclotró i d'altres accelerador de partícules de tipus circular.
- Generador homopolar
- Magnetró
- Propulsor magnetoplasmadinàmic
- Espectròmetre de masses
La força de Lorentz també pot actuar sobre un conductor que transporta un corrent elèctric, en aquest cas s'anomena força de Laplace (vegeu la Llei de Biot-Savart), per efecte de la interacció entre la conducció d'electrons amb els àtoms del material conductor. Aquesta força s'utilitza en dispositius com:
- Railgun o canó elèctric.
- Generador elèctric
- Motor elèctric
Vegeu també[modifica]
Referències[modifica]
- ↑ 1,0 1,1 Huray, Paul G. Maxwell's Equations. Wiley-IEEE, 2010, p. 22. ISBN 978-0-470-54276-7.
- ↑ 2,0 2,1 Per F. Dahl, Flash of the Cathode Rays: A History of J J Thomson's Electron, CRC Press, 1997, p. 10.
- ↑ 3,0 3,1 3,2 Paul J. Nahin, Oliver Heaviside, JHU Press, 2002.
- ↑ Huray, Paul G. Maxwell's Equations (en anglès). John Wiley & Sons, 2009-11-16. ISBN 978-0-470-54276-7.
- ↑ Delon, Michel. Encyclopedia of the Enlightenment. Chicago, IL: Fitzroy Dearborn Publishers, 2001, p. 538. ISBN 157958246X.
- ↑ Goodwin, Elliot H. The New Cambridge Modern History Volume 8: The American and French Revolutions, 1763–93. Cambridge: Cambridge University Press, 1965, p. 130. ISBN 9780521045469.
- ↑ Meyer, Herbert W. A History of Electricity and Magnetism. Norwalk, Connecticut: Burndy Library, 1972, p. 30–31. ISBN 0-262-13070-X.
- ↑ Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. New York: Oxford University Press, 1993, p. 78–79. ISBN 0-19-506488-7.
- ↑ Darrigol, Olivier. Electrodynamics from Ampère to Einstein. Oxford, [England]: Oxford University Press, 2000, p. 9, 25. ISBN 0-19-850593-0.
- ↑ Verschuur, Gerrit L. Hidden Attraction : The History And Mystery Of Magnetism. New York: Oxford University Press, 1993, p. 76. ISBN 0-19-506488-7.
- ↑ Darrigol, Olivier. Electrodynamics from Ampère to Einstein. Oxford, [England]: Oxford University Press, 2000, p. 126–131, 139–144. ISBN 0-19-850593-0.
- ↑ M.A, J. J. Thomson «XXXIII. On the electric and magnetic effects produced by the motion of electrified bodies». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 11, 68, 01-04-1881, pàg. 229–249. DOI: 10.1080/14786448108627008. ISSN: 1941-5982.
- ↑ Darrigol, Olivier. Electrodynamics from Ampère to Einstein. Oxford, [England]: Oxford University Press, 2000, p. 200, 429–430. ISBN 0-19-850593-0.
- ↑ Heaviside, Oliver «On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric». Philosophical Magazine, April 1889, pàg. 324.
- ↑ Lorentz, Hendrik Antoon, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, 1895.
- ↑ Darrigol, Olivier. Electrodynamics from Ampère to Einstein. Oxford, [England]: Oxford University Press, 2000, p. 327. ISBN 0-19-850593-0.
- ↑ Whittaker, E. T.. A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century. Longmans, Green and Co., 1910, p. 420–423. ISBN 1-143-01208-9.




























