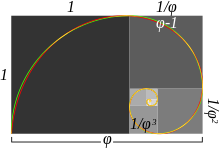
Secció àuria
| Tipus | constant matemàtica, nombre irracional, nombre algebraic, nombre construïble i nombre metàl·lic |
|---|---|
| Propietats | |
| Valor | 1,6180339887499 |
| Altres numeracions | |
| Fórmules | |
| Expressió algebraica | |

La raó àuria, nombre auri, secció àuria o divina proporció és la proporció entre dos segments a i b (o per extensió, entre dues quantitats a i b) que compleixen la condició que la proporció entre la suma d'aquests dos segments[1] i el segment més gran és la mateixa que hi ha entre el segment més gran i el segment més petit. Dit amb unes altres paraules, la suma dels dos segments és al segment gran com el segment gran és al segment petit. Anomenant a el segment (o nombre) gran i b el petit, la fórmula és:
El quocient d'aquestes dues quantitats és un nombre irracional conegut com a nombre auri o nombre d'or, i designat habitualment per la lletra grega Φ o també φ (fi), en honor de Fídies, escultor i arquitecte grec del Partenó, o menys sovint amb τ (tau):
A la cultura occidental s'ha considerat històricament, i de manera consistent, que les formes definides amb la proporció àuria són estèticament agradables. En diferents períodes s'han privilegiat les formes definides amb aquesta proporció, a l'arquitectura, l'art i el disseny. També s'ha fet servir la inversa, expressada com Φ-1. A voltes s'utilitza la fi minúscula (φ) per a la proporció inversa i la majúscula per a la proporció directa.
La proporció àuria es troba recurrentment a la natura. Aquest fet, juntament amb el que tingui unes propietats matemàtiques remarcables, l'ha fet destacar com un camp matemàtic propi.
Història[modifica]
S'ha suposat que l'origen del nombre d'or se situa a la civilització sumèria, tot basant-se en la relació existent entre aquesta proporció i els estels de cinc puntes trobats a les tauletes de fang sumèries del 3200 aC. Tanmateix, res no indica de manera fefaent que aquesta civilització conegués la proporció àuria.
S'han trobat proporcions molt properes a l'àuria a les piràmides de Guiza, cosa que podria indicar que els antics egipcis coneixien el nombre d'or. Però no està clar si el seu ús es deu a un coneixement conscient de les seves propietats estètiques i simbòliques; o per uns altres motius; o per mer atzar.
A l'antiga Grècia es coneixien bé algunes de les seves propietats, descobertes pels pitagòrics, gràcies a la seva freqüent aparició a la geometria. Tanmateix, no sembla cert que en valoressin el seu vessant estètic. Malgrat tot, a molts monuments com el Partenó, hom pot trobar-hi proporcions àuries, o gairebé, molt properes. No està provat, però, que aquestes relacions fossin expressament cercades.
A l'arquitectura romana, també s'hi poden trobar proporcions àuries, però tampoc no s'ha provat que es fessin servir a consciència.
Raons àuries en geometria[modifica]
Secció àuria d'un segment[modifica]

Donat un segment AB, es diu que el punt S constitueix secció àuria del segment AB (o el divideix de forma àuria) si la part més gran és mitjana proporcional (o geomètrica) entre el segment AB i la part petita. Si la part petita és SB, com a la figura, matemàticament això és:
Equivalentment, això passa quan el segment sencer és a la part gran com la part gran és a la petita, p. e.:
L'equivalència entre les definicions es veu, per exemple, multiplicant en creu la segona expressió.
També es veu l'equivalència entre aquestes definicions i la de capçalera: en efecte, si AS mesura a i SB té una mesura b (i llavors AB té una mesura a + b) i tot plegat se substitueix en la segona expressió, s'obté:
La secció àuria del segment en una part gran i una de petita té a més la propietat següent:
- La part petita és segment auri de la part gran, si:
- o bé
- Demostració: si (per ser AS el segment auri de AB), restant a banda i banda s'obté que
- Traient-ne factor comú, i tenint en compte que
- .
- Llavors, , Q.E.D.
- Demostració: si (per ser AS el segment auri de AB), restant a banda i banda s'obté que
Construcció de raons àuries amb regle i compàs[modifica]
- Divisió àuria d'un segment AB donat. Una de les construccions més senzilles és la següent:
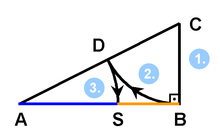
- # Traceu BC, perpendicular a AB per B i de longitud la meitat de AB.
- # Amb centre a C, transporteu la distància CB sobre la hipotenusa CA. S'obté així el punt D.
- # Amb centre a A, transporteu la distància AD sobre el segment AB. La intersecció d'aquest arc amb el segment AB defineix el punt S buscat, que constitueix secció àuria d'AB.
- Construcció del segment AB tal que el seu segment auri és el donat AS. Aquesta és una de les construccions més famoses amb la raó àuria:

- # Traceu SC, perpendicular a AS per S i de longitud igual a AS.
- # Trobeu el punt mitjà M del segment AS (per exemple amb la mediatriu).
- # Amb centre a M, traceu l'arc amb radi MC. La intersecció B d'aquest arc amb la recta suport d'AS defineix el segment cercat AB, el segment auri del qual és AS.
Triangle d'or[modifica]
Els triangles d'or són aquells triangles isòsceles els costats dels quals estan en raó àuria. N'hi ha de dos tipus: els que , que són acutangles i els que , que són obtusangles. Aquests últims sovint són també anomenats triangles d'argent, però no tenen res a veure amb el nombre d'argent (que no té res a veure amb φ, l'invers de Φ).

Els triangles d'or tenen dos angles de 72º i un de 36º; els triangles d'argent tenen dos angles de 36º i un de 108º. Aquests són els mateixos angles que apareixen també en el pentàgon regular i el pentacle, on no és sorprenent de retrobar els triangles d'or i la raó àuria.
- Demostració: a la figura de l'esquerra, es pot veure com el triangle ABD és semblant al triangle BCA, ja que els dos són isòsceles i tenen un angle en comú. Així, els angles ABD i ACB són iguals. La raó de semblança és, per a construcció dels triangles 1/Φ. Llavors, el segment AD mesura 1/Φ.
- Com que el nombre d'or verifica la igualtat
- ,
- el segment DC mesura 1, de manera que el triangle BCD és isòsceles i els angles DCB i DBC són iguals. Per tant, com que DCB i ACB són iguals, ABD i DBC són iguals i DB marca la bisectriu de l'angle ABC. Atès que la suma dels angles d'un triangle val 180°, els valors dels angles és de 36° per als més aguts (la cinquena part d'un angle pla) i de 72º per als més oberts, (dues cinquenes parts de l'angle pla o una cinquena part d'un angle complet).
Rectangle d'or[modifica]

Els rectangles d'or són aquells rectangles els costats dels quals guarden raó àuria.
La construcció d'un rectangle d'or amb compàs es pot fer fàcilment a partir d'un quadrat mitjançant la segona construcció de l'apartat corresponent. Punxant al centre d'un dels costats i obrint fins a un dels dos angles oposats, només cal baixar l'arc fins a la prolongació del costat on s'ha punxat. Una de les propietats dels rectangles d'or és que el rectangle resultant de l'eliminació del quadrat de costat b que el pot generar (vegeu la figura), també és d'or. Aquesta propietat és deguda al fet que la raó àuria compleix la propietat següent, ja vista en apartats anteriors:
- .
El pentàgon i el pentalfa regulars[modifica]

El pentàgon regular i les seves diagonals, que formen una pentalfa (o pentacle) amaguen unes quantes propietats relacionades amb la raó àuria. Alguns creuen que aquest podria ser un dels motius pels quals aquest símbol va ser l'escollit per Pitàgores per a la germandat que creà i presidí: els pitagòrics.
Per tractar-se de pentàgons regulars, s'identifiquen deu angles de 108º, cinc en el pentàgon exterior i cinc més en el format en l'interior. A partir d'aquests deu angles se'n poden trobar cinc més també de 108º (per angles oposats pel vèrtex) i deu angles de 72º (per angles suplementaris. D'aquesta manera, s'identifiquen vint triangles d'or, cinc d'ells formant les puntes del pentacle. També s'hi identifiquen quinze triangles d'argent (de dues mides diferents, cinc petits i deu grans). Només hi ha, doncs, tres tipus d'angles: de 36º, 72º (el doble de 36º) i 108º (el triple).

Pel que fa a longitud de segments, s'observa que només n'hi ha de quatre longituds diferents, però totes en relació àuria amb alguna altra:
- Demostració: per a demostrar cadascuna d'aquestes relacions, només cal trobar un triangle d'or o d'argent format per costats amb les longituds corresponents. Els triangles són efectivament d'or o d'argent perquè ho corroboren els seus angles i la relació n'és àuria per definició de triangle d'or o d'argent.
Espirals d'or[modifica]
Com pot construir, a partir d'una successió de rectangles d'or i quadrats (vegeu la figura), una espiral tot traçant quarts de circumferència dins cada quadrat i tangents a aquest. Aquesta espiral s'aproxima a l'espiral d'or, una espiral logarítmica de centre en la intersecció de les dues diagonals indicades en la figura, punt que s'anomena l'ull de Déu, i d'equació polar:

De la mateixa manera, es pot construir, a partir d'una successió de triangles d'or, una espiral aproximada a la vertadera d'or triangular, també espiral logarítmica, però ara d'equació polar:
Angle d'or[modifica]

S'anomena angle d'or aquell angle obtingut mitjançant la partició d'un cercle (la circumferència del qual té una longitud c) en dos sectors circulars, el més gran amb un arc de longitud a i el menor, amb un arc de longitud b, de manera que:
i prenent com a bo l'angle petit (el de longitud d'arc b).
Com que es tracta d'una partició del cercle, també es té que , i per tant, (vegeu el paral·lelisme amb la secció àuria d'un segment).
- L'angle d'or mesura , o bé en radians,
- Demostració: de l'equació , operant s'arriba a l'equació , de la qual, resolent, s'obté:
- D'aquí, s'obtenen els dos valors següents per a :
- Com que tant a com b són positius, es té que o que . Substituint-ho en , i reordenant s'obté que:
- , d'on s'obté la mesura angular de l'angle: o .
El nombre d'or[modifica]
Propietats[modifica]
Puix que Φ resulta de la solució d'una equació polinòmica, forma part del conjunt dels nombres algebraics. Pot ser demostrat també que Φ és un nombre irracional o incommensurable.
- (vegeu les primeres 20.000 xifres decimals del nombre d'or Arxivat 2005-11-04 a Wayback Machine.)
Com que el seu conjugat és menor que la unitat, també és un nombre de Pisot.
Algunes expressions amb les potències de Φ:
Les potències de Φ també compleixen la propietat següent:
- Demostració: de la propietat anterior pot obtenir-se de multiplicar la igualtat per .
- Així, les potències naturals del nombre d'or compleixen la relació de recurrència de Fibonacci,
- Gràcies a aquesta propietat, es poden també escriure expressions en què s'observa la successió de Fibonacci:
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Una altra propietat sorprenent relacionada amb la recurrència de Fibonacci és que el quocient entre termes consecutius d'una successió definida amb aquesta recurrència, entre aquestes, la successió de Fibonacci, tendeix al nombre d'or. En efecte, si és una successió tal que , llavors:
- Demostració: plantejant el límit,
-
- De , multiplicant per x, s'arriba a:
- , una equació quadràtica ja coneguda amb arrels i . La primera arrel és la corresponent a la part creixent de la successió, Q.E.D. La segona, és la corresponent a una hipotètica successió endarrere (cercant el límit .
Com que , es pot representar Φ en forma de fracció contínua:
El fet que en aquesta fracció contínua només n'apareguin uns fa que el nombre Φ sigui l'irracional més irracional (que convergeix més lentament), cosa que fa que tingui aplicacions interessants en la natura (vegeu l'apartat "El nombre d'or en la natura").
Com que , Φ es pot representar també amb una iteració infinita d'arrels quadrades:
El nombre d'or presenta també propietats interessants si s'utilitza com a base d'un sistema de nombres (vegeu base d'or).
En trigonometria, el nombre d'or està molt relacionat amb els angles que apareixen en un pentacle: (36º, 72º i 108º) i amb les seves meitats: 18º i 54º:
La demostració és en l'article "Constants trigonomètriques exactes, angle de 36º".
El nombre d'or també apareix en expressions com:
La proporció àuria a les arts[modifica]
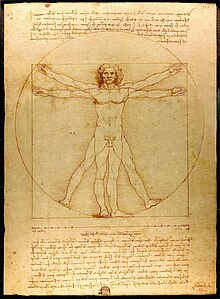
El 1509, Luca Pacioli publicà Divina Proportione, on tractava no només de les curiositats matemàtiques del nombre d'or, sinó també del seu ús a l'arquitectura. Això va propiciar la idea que molts artistes del Renaixement el feien servir. Un bon exemple d'aquests mites és a les pintures de Leonardo Da Vinci, on igual que al Partenó, hom pot trobar-hi relacions àuries, tot i que no hi ha proves de que ho fes expressament.
A mitjans del segle xx, l'arquitecte francosuís Le Corbusier va publicar el llibre Le Modulor, exposant els resultats de la seva recerca sobra una modularITRT que integrés el sistema decimal i el sistema anglosaxó de mesures, basant-se en el nombre d'or. Es especial es dirigia a la seva aplicació en arquitectura, la indústria i l'urbanisme.
S'ha fet servir a construccions més recents com escales o edificis. Potser l'edifici més emblemàtic n'és la seu de l'ONU a Nova York, un gran prisma amb una de les seves cares amb forma de rectangle d'or. Igualment, el sistema de dimensions DIN per a papers, i les seves aplicacions com les targetes de crèdit, es basen o s'acosten al rectangle d'or.
També es fa servir a la música, tant per la durada de les notes (per exemple, pel compositor hongarès Béla Bartók i el francès Olivier Messiaen), com per l'organització de les parts d'una peça (per exemple, a alguna obra del compositor mexicà Silvestre Revueltas), o fins i tot a la relació entre les freqüències de noves notes fora de les escales cromàtiques (per exemple, en For Ann (rising), de James Tenney).
El nombre d'or en la natura[modifica]
El nombre d'or es pot trobar també a la natura, relacionant les coses més diverses:
- A cada rusc d'abelles, la relació entre el nombre de mascles i de femelles.
- A la disposició dels pètals de les flors (anomenada llei de Ludwig).
- A la relació entre els nervis del tall d'una fulla.
- A la disposició de les fulles de moltes plantes, formant una espiral ascendent (les fulles se separen per un angle de 137º 30′ i 28″, angle relacionat amb el nombre d'or), cosa que els permet captar la llum solar sense tapar-se les unes a les altres (es creu que això és a causa del fet que el nombre d'or és el nombre irracional que triga més a convergir, i, per tant, l'efecte que crea aquest angle és precisament el d'evitar que mai les fulles se superposin completament).
- A la relació entre els diàmetres contigus de les pipes de gira-sol.
- A l'espiral dels cargols "nautilus", que són espirals d'or, logarítmiques.
- A les espirals d'una pinya.
- A alguns quasicristalls com el de l'aliatge de zinc, magnesi, i holmi, que són un dodecaedre regular. No és el cas dels cristalls de pirita dodecaèdrics (piritoedres), on les cares són pentàgons amb quatre costats iguals i un de diferent, i la figura resultant té la simetria del tetraedre, anomenada Th (3*2), i no pas pentagonal. Algunes d'aquestes aparicions poden arribar-se a explicar mitjançant les successions recurrents o les propietats geomètriques de la cristal·lització. Altres, però, romanen sense explicació aparent.
Referències[modifica]
- ↑ Diccionario de Arte II (en castellà). Barcelona: Biblioteca de Consulta Larousse. Spes Editorial SL (RBA), 2003, p.124-125. DL M-50.522-2002. ISBN 84-8332-391-5 [Consulta: 5 desembre 2014].
Bibliografia[modifica]
- La proporción áurea, Mario Livio, Editorial Ariel (Barcelona, 2009).
Hrant Arakelyan. Mathématiques et l'histoire de la section d'or. Logos, 2014, 404 p. ISBN 978-5-98704-663-0, (rus).
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Secció àuria |
- La secció àuria: fi Arxivat 2006-12-05 a Wayback Machine.. (anglès)
- Fi, la secció àuria Arxivat 2005-07-20 a Wayback Machine.. (anglès)
- La secció àuria. (anglès)
- Les primeres 20000 xifres decimals del nombre d'or Arxivat 2005-11-04 a Wayback Machine.. (anglès)
- Fi: la proporció divina Arxivat 2008-08-07 a Wayback Machine.. (anglès)
- Fibonacci and the Golden Mean Arxivat 2008-01-26 a Wayback Machine. Vídeo en què s'explica, de manera visual, la relació entre la successió de Fibonacci i el nombre d'or, a més d'altres propietats. (anglès)