Funció gamma
| Gamma | |
|---|---|
 La funció gamma al llarg d'una part de l'eix real | |
| Informació general | |
| Definició general | |
| Camps d'aplicació | Càlcul, anàlisi matemàtica, estadística, física |
En matemàtiques, la funció gamma (també coneguda com a funció gamma completa, per distingir-la de la funció gamma incompleta) és una extensió de la funció factorial, amb el seu argument menys 1, als nombres reals i complexos. Es denota com ,[Nota 1] representada per la lletra majúscula grega Γ.
És a dir, si n és un nombre enter positiu:
- .
La funció gamma està definida per a tots els nombres complexos, excepte els nombres enters no positius. Per als nombres complexos amb una part real positiva, es defineix per una integral impròpia convergent:[1]
- .
Aquesta funció integral s'estén per continuació analítica a tots els nombres complexos, excepte els nombres enters no positius (on la funció té pols simples), obtenint la funció meromorfa que anomenem funció gamma.
La funció gamma no té zero, de manera que la funció gamma inversa és una funció entera. De fet, la funció gamma es correspon amb la transformada de Mellin de la funció exponencial negativa:
- .
La funció gamma és un component en diverses funcions de probabilitat de distribució, i com a tal, és aplicable en els camps de la probabilitat i de l'estadística, així com la combinatòria.
Motivació[modifica]

La funció gamma pot ser vista com una solució per al següent problema d'interpolació:
«Troba una corba suau que uneixi els punts (x, y) donats per y = (x - 1)! en els valors enters positius per a x.»
Un gràfic dels primers factorials deixa clar que es pot fer una corba d'aquest tipus, però seria preferible tenir una fórmula que descrigui amb precisió la corba, en què el nombre d'operacions no depengui del valor de x. La fórmula simple per al factorial x! = 1 × 2 × … × x no es pot utilitzar directament per als valors fraccionaris de x, ja que només és vàlida quan x és un nombre natural (és a dir, un nombre enter positiu). En termes relatius, no hi ha aquest tipus de solucions simples per als factorials; cap combinació finita de sumes, productes, potències, funcions exponencials, o logaritmes serà suficient per expressar x!. L'aproximació de Stirling és asimptòticament igual a la funció factorial per a valors grans de x. És possible trobar una fórmula general per als factorials utilitzant eines com ara integrals i límits per al càlcul. Una bona solució a això és la funció gamma.
Hi ha una infinitat d'extensions contínues del factorial de valors no sencers: es poden extreure un nombre infinit de corbes a través de qualsevol conjunt de punts aïllats. La funció gamma és la solució més útil en la pràctica, sent analítica (excepte en els nombres enters no positius), i pot ser caracteritzada de diverses formes. No obstant això, no és l'única funció analítica que s'estén al factorial, com l'addició a la mateixa de qualsevol funció analítica que és zero en els nombres enters positius, com ara k sin nπ, donarà una altra funció amb aquesta propietat.
Una propietat més restrictiva que satisfà la interpolació superior és satisfer la relació de recurrència definida a una versió traduïda de la funció factorial,
per a x igual a qualsevol nombre real positiu.
El teorema de Bohr-Mollerup demostra que aquestes propietats, juntament amb el supòsit que f sigui logarítmicament convexa (o «súper convexa»),[2] determina de forma única a f per als valors positius i reals. A partir d'aquí, la funció gamma es pot estendre a tots els valors reals i complexos (amb excepció dels nombres enters negatius i el zero) utilitzant l'única continuació analítica de f.
Definició[modifica]
Definició principal[modifica]
La notació es deu al matemàtic Legendre. Si la part real del nombre complex t és positiu (Re(t) > 0), llavors la integral
convergeix absolutament, i es coneix com la integral d'Euler segona espècie (la integral d'Euler de la primera espècie defineix la funció beta). L'ús de la integració per parts, es veu que satisfà l'equació funcional:
Combinant això amb , s'obté:
o
- .
per a .
La identitat Γ(t) = Γ(t + 1)t es pot utilitzar (o, i s'obté el mateix resultat, es pot utilitzar la continuació analítica) per a estendre de forma única la formulació integral per a Γ(t) a una funció meromorfa definida per a tots els nombres complexos t, excepte t = −n per a enters n ≥ 0, on la funció té pols simples amb residu (−1)nn!.
Aquesta és la versió ampliada que es coneix comunament com la funció gamma.
Altres definicions[modifica]
Les següents definicions de productes infinits per a la funció gamma d'Euler i Weierstrass, respectivament, són vàlides per a tots els nombres complexos t, excepte els nombres enters no positius:
on γ ≈ 0,577216… és la constant d'Euler-Mascheroni. És fàcil demostrar que la definició d'Euler satisfà l'equació funcional (1) anterior.
Una curiosa parametrització de la funció gamma es dona en termes de polinomis de Laguerre generalitzats,
que convergeix per Re(t) < 12.
La funció gamma en el pla complex[modifica]

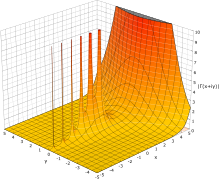
El comportament de per a una variable positiva creixent és simple: creix ràpidament, més ràpid que una funció exponencial. Asimptòticament és com t → ∞, la magnitud de la funció gamma està donada per la fórmula de Stirling
on el símbol ~ vol dir que el quocient de banda i banda convergeix a 1.
El comportament de la t no positiva és més intricada. L'integral d'Euler no convergeix per a t ≤ 0t, però la funció que es defineix en el semiplà positiu complex té una continuació analítica única cap al semiplà negatiu. Una manera de trobar aquesta continuació analítica és l'ús de la integral d'Euler per a arguments positius i estendre el domini als nombres negatius amb l'aplicació reiterada de la fórmula de recurrència,
elegint a n de tal manera que t + n sigui positiu. El producte en el denominador és zero quan t és igual a qualsevol dels nombres enters 0, -1, -2, .... Així, la funció gamma ha de ser indefinida en aquests punts per a la divisió per zero; és una funció meromorfa amb pols simples en els nombres enters no positius.
Els residus de la funció en aquests punts són:
La funció gamma és sempre diferent de zero al llarg de l'eix real, tot i que es tracta arbitràriament prop de zero quan t → −∞. Hi ha, de fet, no hi ha cap nombre complex t per als que , i per tant la funció gamma inversa és una funció sencera, amb zeros en t = 0, −1, −2,…
La funció gamma té un mínim local en xmin ≈ 1,46163, on aconsegueix el valor de Γ(xmin) ≈ 0,885603.
La funció gamma ha d'alternar el signe entre els pols perquè el producte en la recurrència cap endavant conté un nombre imparell de factors negatius si el nombre de pols entre t i t + n és imparell, i un nombre parell si el nombre de pols és parell.
Propietats[modifica]
General[modifica]
Altres equacions funcionals importants per a la funció gamma són la fórmula de reflexió d'Euler
que implica
i la fórmula de duplicació
La fórmula de duplicació és un cas especial del teorema de multiplicació
Una propietat simple però útil, que es pot veure a partir de la definició de límit, és:
Potser el valor més conegut de la funció gamma d'un argument no sencer és
que es pot trobar mitjançant l'establiment de z = 12 en les fórmules de reflexió o duplicació, mitjançant l'ús de la relació amb la funció beta donada a continuació amb x = y = 12, o simplement fent la substitució en la definició d'integral de la funció gama, resultant en una integral de Gauss. En general, per a valors enters no negatius de n tenim:
on n!! denota el doble factorial, quan n = 0, n!! = 1 (Vegeu Valors particulars de la funció gamma per als valors calculats).
Podria ser temptador generalitzar el resultat mitjançant la recerca d'una fórmula per a altres valors individuals de , on r és racional. No obstant això, aquests nombres no són coneguts per ser expressables per si mateixos en termes de funcions elementals. S'ha demostrat que és un nombre transcendent i algebraicament independent de π per a qualsevol nombre enter n i cadascuna de les fraccions de r = 16, 14, 13, 23, 34, 56.[3] En general, quan es calculen els valors de la funció gamma, cal conformar-se amb aproximacions numèriques
Un altre límit útil per a aproximacions asimptòtiques és:
Les derivades de la funció gamma es descriuen en termes de la funció poligamma. Per exemple:
Per a un enter positiu m la derivada de la funció gamma es pot calcular com segueix (aquí γ és la constant d'Euler-Mascheroni):
Per a Re(x) > 0 la n-derivada de la funció gamma és:

La funció gamma té pols simples en z = −n = 0, −1, −2, −3,… El residu es
Els pols i els residus es poden obtenir de la fórmula
A més, la funció gamma té el següent desenvolupament de Laurent en
vàlid per a |z − 1| < 1.
Usant la identitat
amb particions
- ,
tenim, en particular,
- .
Desenvolupament en sèries de Fourier[modifica]
El logaritme de la funció gamma té el següent desenvolupament en sèries de Fourier
que ha estat durant molt de temps atribuït a Ernst Kummer, obtinguda en 1847.[4][5] No obstant això, va ser fa relativament poc que Iaroslav Blagouchine va descobrir que aquesta sèrie va ser obtinguda per primera vegada per Carl Johan Malmsten en 1842.[6]
La fórmula de Raabe[modifica]
En particular, si a = 0 llavors
S'utilitza aquesta fórmula, quan es vol obtenir la versió convergent de la fórmula de Stirling. Usant la regla trapezoïdal completa es pot demostrar que
La funció Pi[modifica]
Una notació alternativa que va ser introduïda originalment per Gauss i que va ser utilitzada de vegades és la funció Pi, que en termes de la funció gamma és
i que per a cada enter no negatiu n.
Utilitzant la fórmula de reflexió de la funció pi, pren la forma
on sinc és la funció sinc normalitzada, mentre que el teorema de multiplicació pren la forma
De vegades també trobem
que és una funció entera, definida per a tot nombre complex, igual que la funció gamma inversa. Que π(z) sigui entera implica que no té pols, pel que Π(z) no té zeros.
El volum d'un n-el·lipsoide amb radis r1, …, rn, pot expressar-se com
Relació amb altres funcions[modifica]
- En la primera integral superior, que defineix la funció gamma, els límits d'integració són fixos. La funció gamma incompleta superior i inferior s'obtenen modificant els límits d'integració superiors o inferiors respectivament.
- La funció gamma està relacionada amb la funció beta per la fórmula
- La derivada logarítmica de la funció gamma és la funció digamma . Les derivades d'ordre superior són les funcions poligamma .
- L'anàleg de la funció gamma sobre un cos finit o un anell finit és el sumatori de Gauss, un tipus de suma exponencial.
- La funció gamma inversa és una funció sencera i ja s'ha estudiat en un apartar específic.
- La funció gamma també es manifesta en una important relació amb la funció zeta de Riemann, ζ(z).
- que és vàlida només per a Re(z) > 1. També apareix en la seva ecuació funcional
- El logaritme de la funció gamma satisfà la següent fórmula de Lerch:
- on ζH és la funció zeta de Hurwitz, ζ és la funció zeta de Riemann i la prima (') denota la diferenciació en la primera variable.
- La funció gamma està íntimament relacionada amb la funció exponencial estirada. Per exemple, els moments d'aquesta funció són
Valors particulars[modifica]
Alguns valors particulars de la funció gamma són:
La funció log-gamma[modifica]
Com que la funció gamma i les funcions factorials creixen tan ràpidament per a grans arguments, molts entorns informàtics inclouen una funció que calcula el logaritme natural de la funció gamma (que sol donar-se amb el nom lgamma o lngamma en entorns de programació o gammaln en fulls de càlcul); aquesta funció creix molt més lentament, i per als càlculs combinatoris permet sumar i restar els seus logaritmes en lloc de multiplicar i dividir valors molt grans.
La funció digamma, que és la derivada d'aquesta funció, també és normalment vista. En el context d'aplicacions tècniques i físiques, per exemple, amb la propagació de les ones, l'equació funcional
s'utilitza sovint, ja que permet determinar valors de la funció en una franja d'amplada d'1 fins a z de la franja veïna. En particular, començant amb una bona aproximació per a una z amb gran part real, un pot anar pas a pas fins a la z desitjada.
Seguint una indicació de Carl Friedrich Gauss, Rocktaschel (1922) proposa per a una aproximació per a una Re(z) gran:
Això es pot utilitzar per a aproximar amb precisió per a z amb una Re(z) més petita a través de (P.E.Böhmer, 1939)
Una aproximació més precisa es pot obtenir mitjançant l'ús de més termes dels desenvolupaments asimptòtics de i , que es basen en l'aproximació de Stirling.
- en |z| → ∞ amb constant |arg(z)| < π.
En una presentació més «natural»:
- en |z| → ∞ amb constant |arg(z)| < π.
Els coeficients dels termes amb k > 1 de z−k + 1 en l'últim desenvolupament són simplement
on Bk són els nombres de Bernoulli.
Propietats[modifica]
El teorema de Bohr-Mollerup estableix que, entre totes les funcions que s'estenen les funcions factorials als nombres reals positius, només la funció gamma és log-convexa, és a dir, el seu logaritme natural és convex en l'eix real positiu.

D'alguna manera, la funció és la forma més natural; que fa que alguns dels atributs intrínsecs de la funció més clara. Un exemple notable és la sèrie de Taylor de en 1:
amb ζ(k) denotant la funció zeta de Riemann en k.
Per tant, utilitzant la següent propietat:
podem trobar la representació integral de la funció :
o, establint z = 1 i calculant γ:
Integració sobre log-gamma[modifica]
La integral es pot expressar en termes de la funció G-Barnes:[Nota 5][7][8]
on Re(z) > −1.
També es pot escriure en termes de la funció zeta de Hurwitz:[9][10]
Aproximacions[modifica]
Els valors complexos de la funció gamma es poden calcular numèricament amb precisió arbitrària usant l'aproximació de Stirling, l'aproximació de Lanczos o l'aproximació de Spouge.
La funció gamma es pot calcular amb precisió fixa per a Re(z) ∈ [1,2] mitjançant l'aplicació de la integració per parts de la integral d'Euler. Per a qualsevol nombre positiu x la funció gamma es pot escriure
Quan Re(z) ∈ [1,2] i x ≥ 1, el valor absolut de l'última integral és menor que (x + 1)e−x. Per a triar una gran x suficient, aquesta última expressió es pot fer més petita que 2−N per a qualsevol valor N desitjat. Per tant, la funció gamma es pot avaluar a N parts de precisió amb la sèrie anterior.
L'únic algorisme ràpid per al càlcul de la funció gamma d'Euler per a qualsevol argument algebraic (incloent el racional) va ser construït per E.A. Karatsuba.[11][12][13]
Per arguments que són múltiples sencers d' 124, la funció gamma també es pot avaluar de forma ràpida utilitzant iteracions amb mitjanes aritmètiques-geomètriques (veure valors particulars de la funció gamma).
Aplicacions[modifica]
Obrint una pàgina a l'atzar en una taula avançada de fórmules, és més probable de situar la funció gamma com una funció trigonomètrica. Un autor descriu la funció gamma com «es podria dir que és la funció especial més comú, o la menys especial d'elles. Les altres funcions transcendents [...] es diuen especials, perquè es podrien evitar algunes d'elles de mantenir-se allunyades de molts temes matemàtics especialitzats. D'altra banda, la funció gamma és més difícil d'evitar.»[14]
Els problemes d'integració[modifica]
La funció gamma troba aplicacions en àrees tan diverses com la física quàntica, l'astrofísica i la dinàmica de fluids [15] La distribució gamma, que es formula en termes de la funció gamma, s'utilitza en les estadístiques per modelar una àmplia gamma de processos ; per exemple, el temps entre les ocurrències dels terratrèmols.[16]
La raó principal de la utilitat funció gamma en aquests contexts és la prevalença d'expressions del tipus f(t) e−g(t) que descriuen els processos que decauen exponencialment en el temps o en l'espai. Les integrals de tals expressions de tant en tant es poden resoldre en termes de la funció gamma quan no hi ha una solució primària. Per exemple, si f és una funció de potència i g és una funció lineal, un simple canvi de variables dona l'avaluació
El fet que la integració es porta a terme al llarg de tot l'eix real positiu podria significar que la funció gamma descriu l'acumulació d'un procés depenent del temps que continua indefinidament, o el valor podria ser el total d'una distribució en un espai infinit.
Per descomptat, és freqüentment útil prendre límits d'integració diferents de 0 i per a descriure l'acumulació d'un procés finit, en aquest cas la funció gamma comuna ja no és una solució; la solució es diu funció gamma incompleta (la funció gamma ordinària, obtinguda mitjançant la integració en tota l'eix real positiu, de vegades diu funció gamma completa per a diferenciar).
Una categoria important de les funcions de forma exponencial decreixent són les funcions gaussianes
i les seves integrals, com ara la funció d'error. Hi ha moltes interrelacions entre aquestes funcions i la funció gamma; en particular que s'obté mitjançant l'avaluació de , és el mateix que es troba en el factor de normalització de la funció d'error i de la distribució normal.
Les integrals que hem discutit fins ara impliquen funcions transcendentals, però la funció gamma també sorgeix de les integrals de funcions purament algebraiques. En particular, les longituds d'arc de l'el·lipse i de la lemniscata, que són corbes definides per equacions algebraiques, estan donades per les integrals el·líptiques que, en casos especials poden ser avaluades en termes de la funció gamma. La funció gamma també es pot utilitzar per a calcular el volum i la superfície de n-esferes.
Un altre cas especial important és la de la funció beta
Càlcul de productes[modifica]
La capacitat de la funció gamma de generalitzar productes factorials porta immediatament a aplicacions en moltes àrees de les matemàtiques; en combinatòria, i per extensió en àrees com la teoria de la probabilitat i el càlcul de les sèries de potències. Moltes expressions que continguin els productes de nombres enters successius es poden escriure com una combinació de factorials; l'exemple més important pot ser la del coeficient binomial.
L'exemple de coeficients binomials es motiva perquè les propietats de la funció gamma quan s'estén als nombres negatius naturals. Un coeficient binomial dona el nombre de formes de triar k elements d'un conjunt de n elements; si k > n, no és possible. Si k > n, ((n − k)! és el factorial d'un enter negatiu i per tant infinit si utilitzem la definició de la funció gamma de factorials; dividint per infinit dona el valor esperat de 0.
Podem reemplaçar el factorial per una funció gamma per a estendre aquesta fórmula als nombres complexos. En general, això funciona per a qualsevol producte en el qual cada factor és una funció racional de l'índex variable, al factoritzar la funció racional en expressions lineals. Si P i Q són polinomis mònics de grau m i n amb les respectives arrels p1, …, pm i q1, …, qn, tenim
Si tenim una manera de calcular la funció gamma numèricament, és molt fàcil de calcular els valors numèrics d'aquests productes. El nombre de funcions gamma en el costat dret depèn només del grau dels polinomis, per la qual cosa no importa si b − a és igual a 5 o 10⁵. D'altra banda, a causa dels pols de la funció gamma, l'equació també es porta a terme (en el sentit d'obtenir límits) quan el producte de l'esquerra conté zeros o pols.
Mitjançant l'adopció de límits, determinats productes racionals amb infinits factors també poden ser avaluats en termes de la funció gamma. A causa del teorema de factorització de Weierstrass, les funcions analítiques es poden escriure com a productes infinits, i aquests de vegades poden ser representats com a productes finits o quocients de la funció gamma. A partir d'aquesta fórmula, la funció exponencial, així com totes les funcions trigonomètriques i funcions hiperbòliques es poden expressar en termes de la funció gamma.
Moltes funcions, incloent la sèrie hipergeomètrica i els casos especials d'aquesta, pot ser representat per mitjà d'integrals de contorn complexes de productes i quocients de la funció gamma, anomenades integrals Mellin-Barnes.
Càlcul fraccionari[modifica]
La n-èsima derivada de (on és un nombre natural) es pot veure de la següent manera:
com
llavors
on pot ser qualsevol nombre on gamma pot estar definit o es pugui definir mitjançant límits.
D'aquesta manera es pot calcular per exemple, la 1/2 derivada de , de i fins i tot d'una constant:
La teoria analítica de nombres[modifica]
Una aplicació elegant i profunda de la funció gamma és en l'estudi de la funció zeta de Riemann. Una propietat fonamental de la funció zeta de Riemann és la seva equació funcional:
Entre altres coses, això proporciona una manera explícita per a la continuació analítica de la funció zeta d'una funció meromórfica en el pla complex i condueix a una prova immediata que la funció zeta té un nombre infinit de zeros anomenats «trivials» en la recta real. Borwein va anomenar a aquesta fórmula «una de les més belles troballes en les matemàtiques».[17] Un altre defensor d'aquest títol podria ser
Totes dues fórmules van ser derivades per Bernhard Riemann en la seva obra escrita en 1859 «Über die Anzahl der Primzahlen unter einer gegebenen Größe» (sobre els nombres primers per sota d'una determinada mida), una de les fites en el desenvolupament de la teoria analítica de nombres (la branca de les matemàtiques que estudia els nombres primers utilitzant les eines d'anàlisi matemàtica). Els nombres factorials, considerats com a objectes discrets, són en concepte importants en la teoria de nombres clàssica, ja que contenen molts factors primers, però Riemann va trobar un ús per a la seva extensió contínua que podria dir-se que va resultar ser encara més important.
Història[modifica]
La funció gamma ha captat l'interès d'alguns dels matemàtics més destacats de tots els temps. La seva història, sobretot documentada per Philip J. Davis en un article que li va valer el Premi Chauvenet de 1963, reflecteix moltes de les principals novetats dins de les matemàtiques des del segle xviii. En paraules de Davis, «cada generació ha trobat alguna cosa interessant a dir sobre la funció gamma. Potser la propera generació també ho farà.»[18]
Segle XVIII: Euler i Stirling[modifica]

Aparentment, els primers en considerar el problema de desenvolupar el factorial d'arguments no sencers van ser Daniel Bernoulli i Christian Goldbach en la dècada de 1720, i es va resoldre a finals de la mateixa dècada per Leonhard Euler.
Euler va donar dues definicions diferents: la primera no va ser la seva integral integrant, si no un producte infinit,
el qual va informar a Goldbach en una carta de data 13 d'octubre de 1729. Va escriure a Goldbach de nou el 8 de gener de 1730, per a anunciar el seu descobriment de la representació integral
que és vàlida per a n > 0. Pel canvi de variable t = −ln s, això es converteix en la familiar integral d'Euler. Euler va publicar els seus resultats en el document «De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt» (Sobre les progressions transcendentals o les condicions generals donades de forma algebraica), presentat a l'Acadèmia de Sant Petersburg al 28 de novembre de 1729.[19] A més, Euler va descobrir algunes de les propietats funcionals importants de la funció gamma, incloent la fórmula de la reflexió.
James Stirling, un contemporani d'Euler, també va tractar de trobar una expressió contínua per al factorial i es va acostar amb el que actualment es coneix com la fórmula de Stirling. Tot i que la fórmula de Stirling dona una bona estimació de n!, també per als no sencers, no proporciona el valor exacte. Les extensions d'aquesta fórmula que corregeix l'error van ser donades per Stirling, junt amb Jacques Philippe Marie Binet.
Segle xix: Gauss, Weierstrass i Legendre[modifica]

Carl Friedrich Gauss va tornar a escriure el producte d'Euler com
i va utilitzar aquesta fórmula per a descobrir noves propietats de la funció gamma. Tot i que Euler va ser un pioner en la teoria de variables complexes, sembla que no va tenir en compte el factorial d'un nombre complex, ja que el primer en fer-ho va ser Gauss.[20] Gauss també va demostrar el teorema de multiplicació de la funció gamma i va investigar la relació entre la funció gamma i les integrals el·líptiques.
Karl Weierstrass va establir a més el paper de la funció gamma en l'anàlisi complexa, a partir d'una altra representació del producte,
on γ és la constant d'Euler-Mascheroni. Weierstrass va escriure originalment el seu producte com un per a , en aquest cas es pren sobre els zeros de la funció en lloc dels seus pols. Inspirat per aquest resultat, va demostrar el que es coneix com el teorema de factorització de Weierstrass, que qualsevol funció sencera pot ser escrita com un producte sobre els seus zeros en el pla complex; una generalització del teorema fonamental de l'àlgebra.
El nom de la funció gamma i el símbol van ser introduïts per Adrien-Marie Legendre cap 1811; Legendre també va reescriure la definició integral d'Euler en la seva forma moderna. Tot i que el símbol és una gamma grega majúscula, no existeix un estàndard acceptat per si el nom de la funció ha de ser escrit com «funció gamma» o «funció Gamma» (alguns autors escriuen simplement «funció »). La notació alternativa «funció pi», Π(z) = z!, va ser creada per Gauss i de vegades es troba en la literatura més antiga, però la notació de Legendre és la dominant en les obres modernes.
Està justificat preguntar-se per què es distingeix entre els factorials ordinàris i la funció gamma mitjançant l'ús de símbols diferents, i en particular per què la funció gamma s'ha d'ajustar al tipus en comptes de fer servir .
Tinguem en compte que la notació per als exponents, xn, s'ha generalitzat entre nombres enters als nombres complexos xz sense cap canvi. El motiu de Legendre per a la normalització és desconegut, i ha estat criticat per alguns com a incòmode (el matemàtic del segle xx Cornelius Lanczos, per exemple, el va qualificar com "buit de qualsevol racionalitat" i en el seu lloc s'hauria d'utilitzar z!).[21]
La normalització de Legendre simplifica algunes fórmula, però complica la majoria d'altres. Des d'un punt de vista modern, la normalització de Legendre de la funció gamma és la integral del caràcter additiu e−x en contra del caràcter multiplicador xz respecte a la mesura de Haar dxx en el grup de Lie R+. Per tant aquesta normalització fa que sigui més clar que la funció gamma és un anàleg continu del sumatori de Gauss.
Segles XIX – XX: la caracterització de la funció gamma[modifica]
És problemàtic que s'hagin donat un gran nombre de definicions per a la funció gamma. Tot i que descriuen la mateixa funció, no és del tot senzill demostrar l'equivalència. Stirling mai va demostrar que la seva fórmula estesa corresponia exactament a la funció gamma d'Euler; una primera prova la va donar Charles Hermite en 1900.[22] En lloc de trobar una prova especialitzada per a cada fórmula, seria desitjable disposar d'un mètode general per a la identificació de la funció gamma.
Una manera de provar seria trobar una equació diferencial que caracteritza la funció gamma. La majoria de les funcions especials en les matemàtiques aplicades sorgeixen com solucions a les equacions diferencials, les solucions són úniques. No obstant això, la funció gamma no apareix per adaptar-se a qualsevol equació diferencial simple. Otto Hölder va demostrar en 1887 que la funció gamma, almenys, no satisfà cap equació diferencial algebraica al mostrar que una solució a una equació no podia satisfer la fórmula de recurrència de la funció gamma, pel que és una funció hipertranscendental. Aquest resultat es coneix com el teorema de Hölder.
No es va donar una caracterització definitiva i d'aplicació general de la funció gamma fins a 1922. Harald Bohr i Johannes Mollerup van demostrar, amb el que es coneix com el teorema de Bohr-Mollerup, que la funció gamma és l'única solució de la relació de recurrència factorial que és positiva i logarítmicament convexa per z positiu i el valor en 1 és 1 (una funció logarítmica és convexa si el seu logaritme és convex). El teorema de Bohr-Mollerup és útil perquè és relativament fàcil de demostrar la convexitat logarítmica per a qualsevol de les diferents fórmules usades per a definir la funció gamma.
Prenent les coses encara més, en lloc de definir la funció gamma per a cap fórmula en particular, podem triar les condicions del teorema de Bohr-Mollerup com la definició, i després recollir qualsevol fórmula que ens agradi i que reuneixi les condicions necessàries com un punt de partida per a l'estudi de la funció gamma. Aquest mètode va ser utilitzat pel grup Bourbaki.
Taules de referència i programari[modifica]
Tot i que la funció gamma es pot calcular pràcticament tan fàcilment com qualsevol funció matemàtica més simple amb un modern ordinador, fins i tot amb una calculadora de butxaca programable, no sempre ha sigut així. Fins a la meitat del segle xx, els matemàtics es van basar en les taules fetes a mà; en particular, en el cas de la funció gamma, amb una taula calculada per Gauss en 1813 i una altra calculada per Legendre en 1825.

Les taules de valors complexos de la funció gamma, així com els gràfics dibuixats a mà, es donen en les Taules de funcions superiors fetes per Jahnke i Emde, publicat per primera vegada en Alemanya en 1909. D'acord amb Michael Berry, «la publicació de J&E d'un gràfic tridimensional que mostra els pols de la funció gamma en el pla complex ha adquirit un estatus gairebé icònic.»[23]
De fet, hi havia poca necessitat pràctica per a qualsevol cosa per als valors reals de la funció gamma, fins a la dècada de 1930, quan es van descobrir les aplicacions de la funció gamma complexa en la física teòrica. Com es va disposar d'equips electrònics per a la producció de taules en la dècada de 1950, es van publicar diverses taules àmplies per a la funció gamma per a satisfer la demanda, que va inclore una taula amb precisió de 12 decimals de l'Institut Nacional de Normes i Tecnologia dels Estats Units.[18] Abramowitz i Stegun es va convertir en la referència estàndard per a aquesta i moltes altres funcions especials després de la seva publicació en 1964.
Les implementacions de doble precisió de coma flotant de la funció gamma i del seu logaritme estan actualment disponibles en la majoria de les biblioteques de programari de computació científica i funcions especials, per exemple, TK Solver, Matlab, GNU Octave, i la GNU Scientific Library. La funció gamma també es va agregar a la biblioteca estàndard de C (math.h). Les implementacions de precisió arbitrària estan disponibles en la majoria dels sistemes d'àlgebra computacional, com ara Mathematica i Maple. PARI/GP, MPFR i MPFUN també contenen implementacions lliures de precisió arbitrària.
Notes[modifica]
- ↑ La notació va ser ideada per Adrien-Marie Legendre
- ↑
Trobar és fàcil:
Després s'obté una fórmula per com una funció de :
Fem servir integració per parts per resoldre la integral:
En el límit inferior s'obté directament .
En l'infinit, usant la regla de L'Hôpital vegades: , pel que s'anul·la el primer terme, , el que ens dona el següent resultat: ; la part dreta de l'equació és exactament , amb el que hem obtingut una relació de recurrència: . - ↑ Això es pot derivar diferenciant la forma integral de la funció gamma pel que fa a x, i l'ús de la tècnica de la diferenciació sota el signe integral.
- ↑ Això es pot veure mitjançant el desenvolupament de exp(-t)
- ↑ Vegeu la funció G-Barnes per a provar.
Referències[modifica]
- ↑ Greenberg, Michael D. Advanced Engineering Mathematics (en anglès). 2a. Upper Saddle River, Nova Jersey: Prentice Hall, 1998, p. 223. ISBN 0-13-321431-1.
- ↑ Kingman, J.F.C. 1961. A convexity property of positive matrices. Quart. J. Math. Oxford (2) 12,283-284.
- ↑ Waldschmidt, M. (2006). "Transcendence of Periods: The State of the Art Arxivat 2012-04-17 a Wayback Machine.". Pure and Applied Mathematics Quarterly, Volume 2, Number 2, 435—463 (PDF copy published by the author)
- ↑ Harry Bateman i Arthur Erdélyi Higher Transcendental Functions [in 3 volumes]. Mc Graw-Hill Book Company, 1955.
- ↑ H.M. Srivastava and J. Choi Series Associated with the Zeta and Related Functions. Kluwer Academic Publishers. The Netherlands, 2001
- ↑ Iaroslav V. Blagouchine Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results. The Ramanujan Journal, vol. 35, no. 1, pp. 21-110, 2014. PDF
- ↑ "W. P. Alexejewsky, Ueber eine Classe von Funktionen, die der Gammafunktion analog sind, Leipzig Weidmanncshe Buchhandluns,46, (1894), 268-275"
- ↑ "E. W. Barnes, The theory of the G-function, Quart. J. Math., 31,(1899), 264-314"
- ↑ Victor S. Adamchik, Polygamma functions of negative order,Journal of Computational and Applied Mathematics, Volume 100, Issue 2, 21 December 1998, Pages 191-199, doi:10.1016/S0377-0427(98)00192-7
- ↑ R.W. Gosper, ., In special functions, q-series and related topics, Amer.Math.Soc. 14 (1997).
- ↑ E.A. Karatsuba, Fast evaluation of transcendental functions. Probl. Inf. Transm. Vol.27, No.4, pp.339-360 (1991).
- ↑ E.A. Karatsuba, On a new method for fast evaluation of transcendental functions. Russ. Math. Surv. Vol.46, No.2, pp.246-247 (1991).
- ↑ E.A. Karatsuba "Fast Algorithms and the FEE Method".
- ↑ Michon, G. P. "Trigonometry and Basic Functions Arxivat 2010-01-09 a Wayback Machine.". Numericana. Retrieved May 5, 2007.
- ↑ Chaudry, M. A. & Zubair, S. M. (2001). On A Class of Incomplete Gamma Functions with Applications. p. 37
- ↑ Rice, J. A. (1995). Mathematical Statistics and Data Analysis (Second Edition). p. 52–53
- ↑ Borwein, J., Bailey, D. H. & Girgensohn, R.. Experimentation in Mathematics. A. K. Peters, 2003, p. 133. ISBN 1-56881-136-5.
- ↑ 18,0 18,1 Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function", The American Mathematical Monthly, Vol. 66, No. 10 (Dec., 1959), pp. 849–869 [1] Arxivat 2012-11-07 a Wayback Machine.
- ↑ Euler's paper was published in Commentarii academiae scientiarum Petropolitanae 5, 1738, 36–57. See E19 -- De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt, from The Euler Archive, which includes a scanned copy of the original article. An English translation Arxivat 2016-03-03 a Wayback Machine. by S. Langton is also available.
- ↑ Remmert, R., Kay, L. D. (translator). Classical Topics in Complex Function Theory. Springer, 2006. ISBN 0-387-98221-3.
- ↑ Lanczos, C. (1964). "A precision approximation of the gamma function." J. SIAM Numer. Anal. Ser. B, Vol. 1.
- ↑ Knuth, D. E.. The Art of Computer Programming, volume 1 (Fundamental Algorithms). Addison-Wesley, 1997.
- ↑ Berry, M. "Why are special functions special?". Physics Today, April 2001
Bibliografia[modifica]
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 6)
- G. E. Andrews, R. Askey, R. Roy, Special Functions, Cambridge University Press, 2001. ISBN 978-0-521-78988-2. Chapter one, covering the gamma and beta functions, is highly readable and definitive.
- Emil Artin, "The Gamma Function", in Rosen, Michael (ed.) Exposition by Emil Artin: a selection; History of Mathematics 30. Providence, RI: American Mathematical Society (2006).
- Birkhoff, George D. «Note on the gamma function». Bull. Amer. Math. Soc., 20, 1913, pàg. 1-10. DOI: 10.1090/s0002-9904-1913-02429-7.
- P. E. Böhmer, ´´Differenzengleichungen und bestimmte Integrale´´, Köhler Verlag, Leipzig, 1939.
- Philip J. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function," American Mathematical Monthly 66, 849-869 (1959)
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP. «Section 6.1. Gamma Function». A: Numerical Recipes: The Art of Scientific Computing. 3rd. Nova York: Cambridge University Press, 2007. ISBN 978-0-521-88068-8.
- O. R. Rocktaeschel, ´´Methoden zur Berechnung der Gammafunktion für komplexes Argument``, University of Dresden, Dresden, 1922.
- Nico M. Temme, "Special Functions: An Introduction to the Classical Functions of Mathematical Physics", John Wiley & Sons, New York, ISBN 0-471-11313-1,1996.
- E. T. Whittaker and G. N. Watson, A Course of Modern Analysis. Cambridge University Press (1927; reprinted 1996) ISBN 978-0-521-58807-2
Vegeu també[modifica]
- Aproximació de Spouge
- Constant de Gauss
- Desigualtat de Gautschi
- Distribució gamma
- Funció digamma
- Funció gamma el·líptica
- Funció gamma incompleta
- Funció gamma inversa
- Funció gamma múltiple
- Funció gamma multivariant
- Funció poligamma
- Funció q-gamma
- Factorial
- Factorial ascendent
- Sumatori de Gauss
- Valors particulars de la funció gamma
- Volum d'una n-esfera (un exemple de la funció gamma que apareix en un problema aparentment no relacionat)
Enllaços externs[modifica]
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Funció gamma |
- NIST Digital Library of Mathematical Functions:Gamma function
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
- C++ reference for std::tgamma
- Michiel Hazewinkel (ed.). Gamma function. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4.
- Aquest article conté material de l'article «Funció gamma» de Citizendium, que es troba sota la llicència de Creative Commons Reconeixement-Compartir Igual 3.0 No adaptada però no sota la GFDL.





























![{\displaystyle {\begin{aligned}\Gamma \left({\tfrac {1}{2}}+n\right)&={(2n)! \over 4^{n}n!}{\sqrt {\pi }}={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }}={\sqrt {\pi }}\left[{n-{\frac {1}{2}} \choose n}n!\right]\\\Gamma \left({\tfrac {1}{2}}-n\right)&={(-4)^{n}n! \over (2n)!}{\sqrt {\pi }}={\frac {(-2)^{n}}{(2n-1)!!}}{\sqrt {\pi }}={\frac {\sqrt {\pi }}{{-{\frac {1}{2}} \choose n}n!}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/727d1d11e799781ba34e570d4207afc9ee30fc5b)





















































































![{\displaystyle \int _{0}^{\infty }e^{-x}x^{n}dx=\left[{\frac {-x^{n}}{e^{x}}}\right]_{0}^{\infty }+n\int _{0}^{\infty }e^{-x}x^{n-1}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b863f56f41b5433a28d741027009c3cf6e4dbc9)


![{\displaystyle \left[{\frac {-x^{n}}{e^{x}}}\right]_{0}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/945b628f3a74978a06f4727b3150c380b841b99f)



